Derivatives & Exchange

Derivatives

Strategies

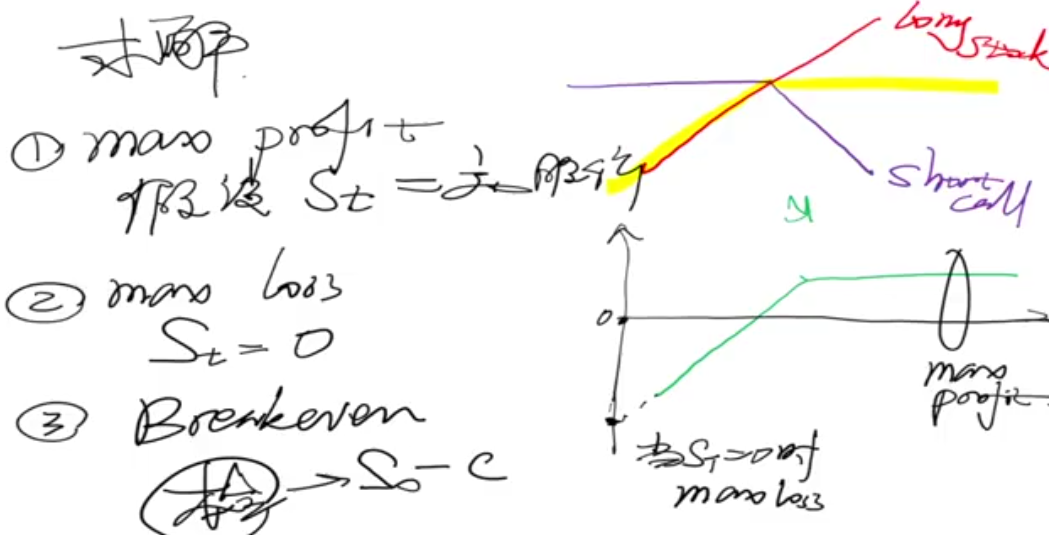
1. Covered Call Strategy (long Stock, short Call)

i.e. $S=2000$$S=2000$

• Yield Enhancement 为长期持有, $K=3000$$K = 3000$

  write a OTM call option.

• Reduce a Position 为了卖, $K=1800$$K=1800$

• Target Price Realisation 近期到期 combine of above two $K=2500$$K=2500$

As the covered call strategy is (long S, short Call)

$Profit=\underset{longS}{\underbrace{(S_T-S_0)}}+\underset{LongCall}{\underbrace{C-max(S_T-K,0)}}$$Profit = \underbrace{(S_T - S_0)}_{long \ S} + \underbrace{ C - \max(S_T-K,0)}_{Long\ Call}$

• if $S_T>K$$S_T > K$, then, $Profit=K-S_0+C$$Profit = K - S_0 + C$ (行权)

• if $S_T\le K$$S_T \leq K$, then, $Profit=S_T-S_0+C$$Profit = S_T -S_0 + C$ (不行权)

• if Break-even, $S_T-S_0+C=0$$S_T - S_0 + C =0$

• if max loss, $S_T=0$$S_T = 0$, $Loss(Profit)=-S_0+C$$Loss (Profit) = -S_0 + C$

• if max gain, $S_T>X$$S_T > X$, $Gain(Profit)=K-S_0+C$$Gain (Profit) = K - S_0 + C$

2. Protected Put (long Stock, long Put)

$Profit=\underset{longStock}{\underbrace{(S_T-S_0)}}+\underset{LongPut}{\underbrace{max(K-S_T,0)-P}}$$Profit = \underbrace{(S_T - S_0)}_{longStock} + \underbrace{\max(K - S_T,0) - P}_{LongPut}$

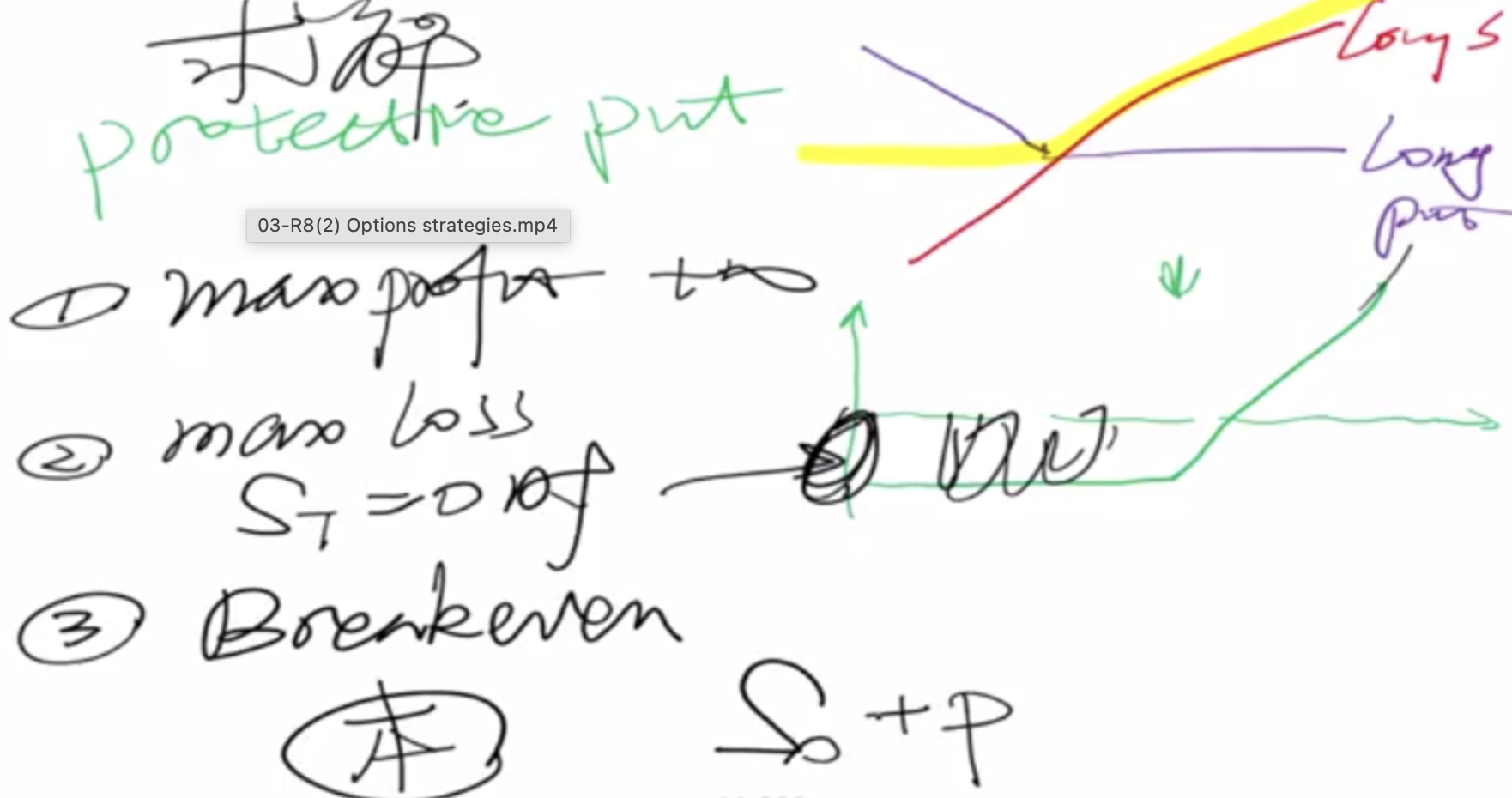
Protected Put is a hedge, but is not a perfect hedge, because there is still the maximum loss part.

3. Collar (long Stock, long Put, short Call, options are all out-the-money OTM)

$Profit=\underset{LongStock}{\underbrace{(S_T-S_0)}}+\underset{ShortCall}{\underbrace{C-max(S_T-K)}}+\underset{LongPut}{\underbrace{max(K-S_T,0)-P}}$$Profit = \underbrace{(S_T - S_0)}_{LongStock} + \underbrace{C - \max(S_T-K)}_{Short Call} + \underbrace{\max(K-S_T,0)-P}_{LongPut}$

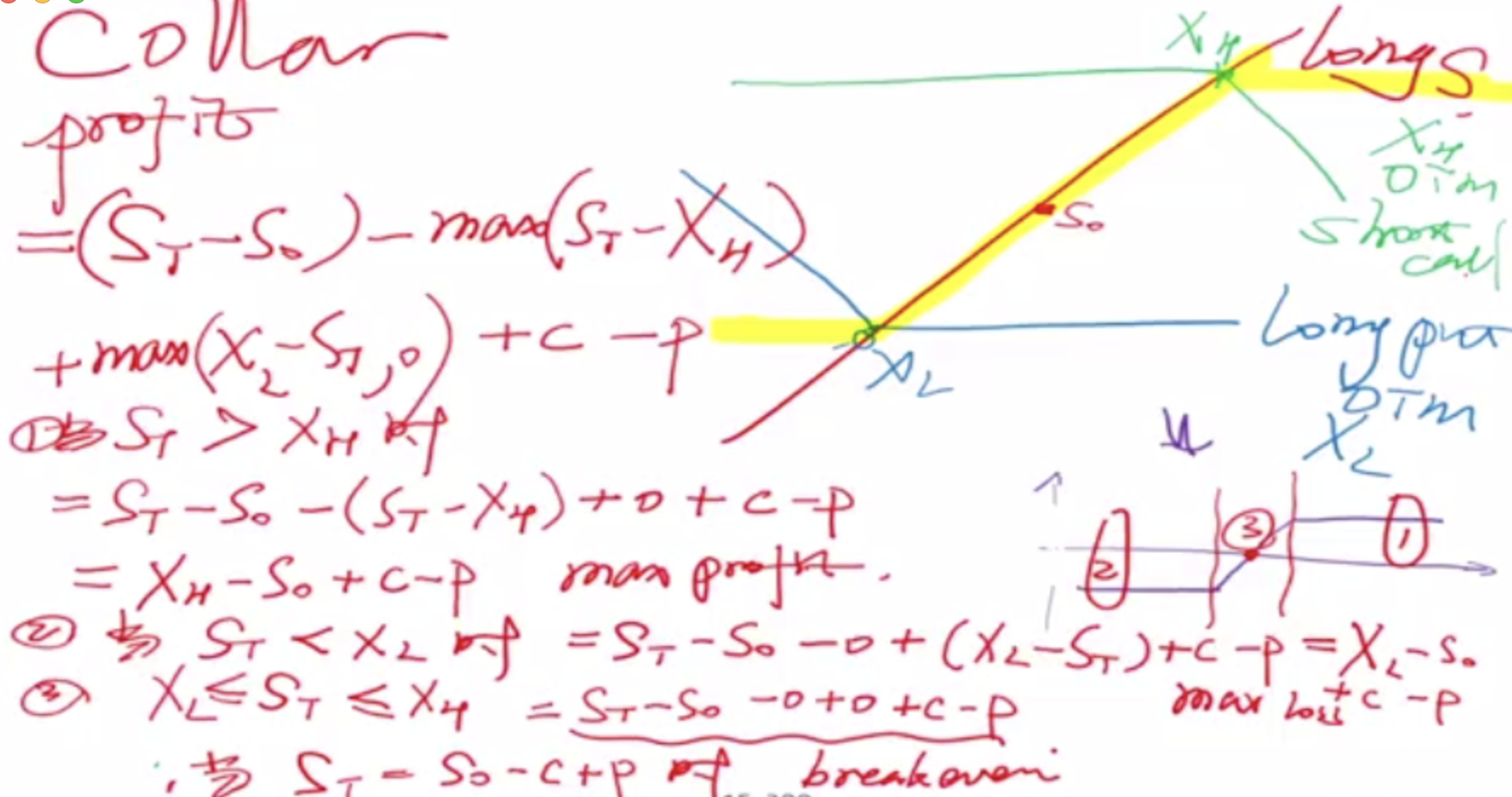
P.S. Put-Call Parity

• Case 1:

  $C+\frac{K}{1+r}=P+S$$C+ \frac{K}{1+r} = P + S$

  Fiduciary Call = Protective Put

• Case 2:

  $S-C=\frac{K}{1+r}-P$$S-C = \frac{K}{1+r} -P$

  Covered Call = Cash Secured Put

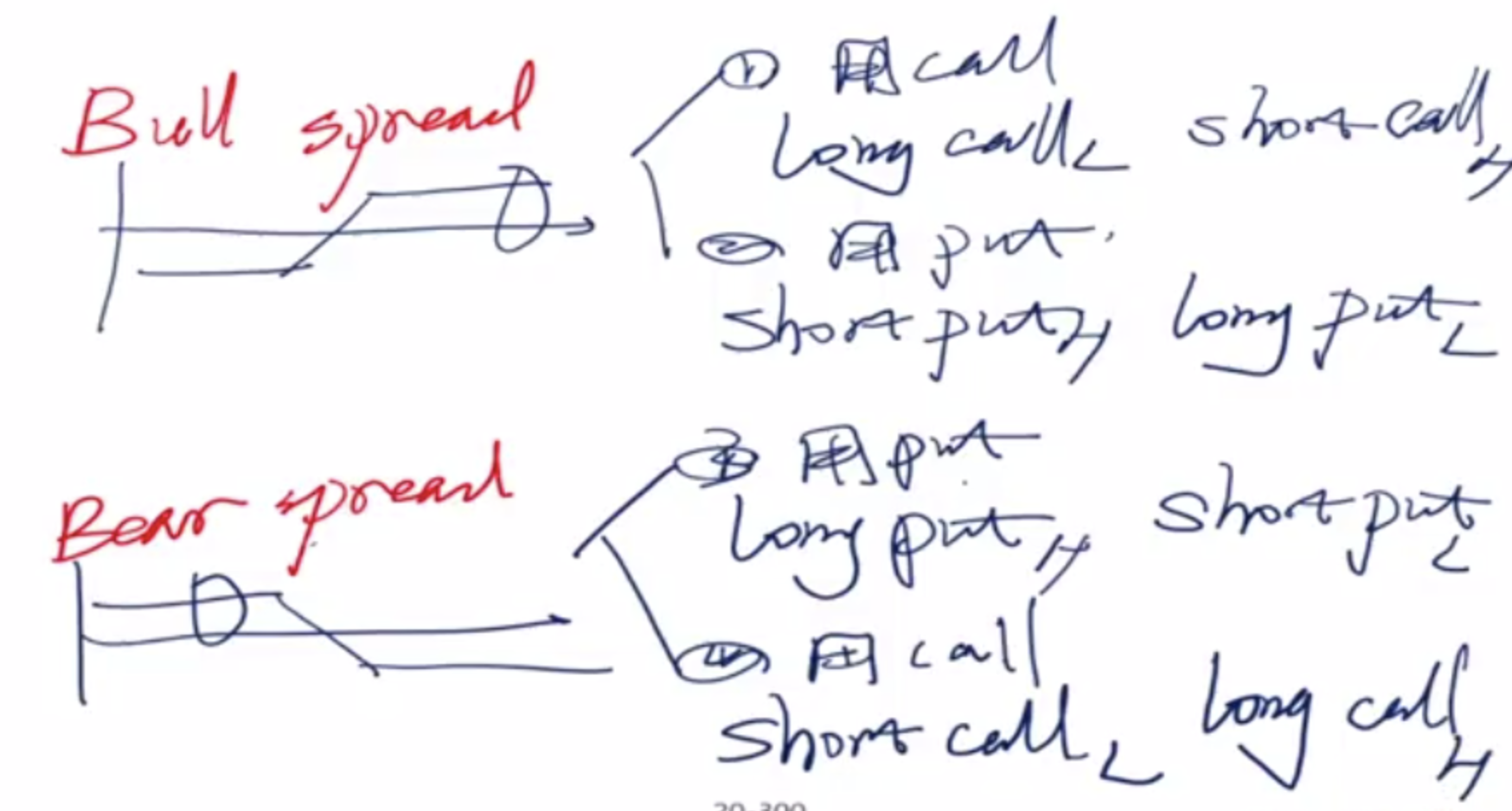
4. Vertical Arbitrage (different exercise price X/K)

• Bull Spread:

  • long $Cal{l}_L$$Call_L$ short $Cal{l}_H$$Call_H$

  • Short $Pu{t}_H$$Put_H$ long $Pu{t}_L$$Put_L$

• Bear Spread:

  • long $Pu{t}_H$$Put_H$ short $Pu{t}_L$$Put_L$

  • Short $Cal{l}_L$$Call_L$ long $Cal{l}_H$$Call_H$

P.S. 如果 options 是 out-of-money，那么是 期权费之差。如果 option 是 in-the-money， 那么还要考虑行权价格的差 + 期权费。总之，现推导。

5. Horizontal Arbitrage (different Expire Date)

• Long Calendar: 买长期 long $Cal{l}_{longer}$$Call_{longer}$ short $Cal{l}_{shorter}$$Call_{shorter}$

• Short Calendar: 买短期 long $Cal{l}_{shorter}$$Call_{shorter}$ short $Cal{l}_{longer}$$Call_{longer}$

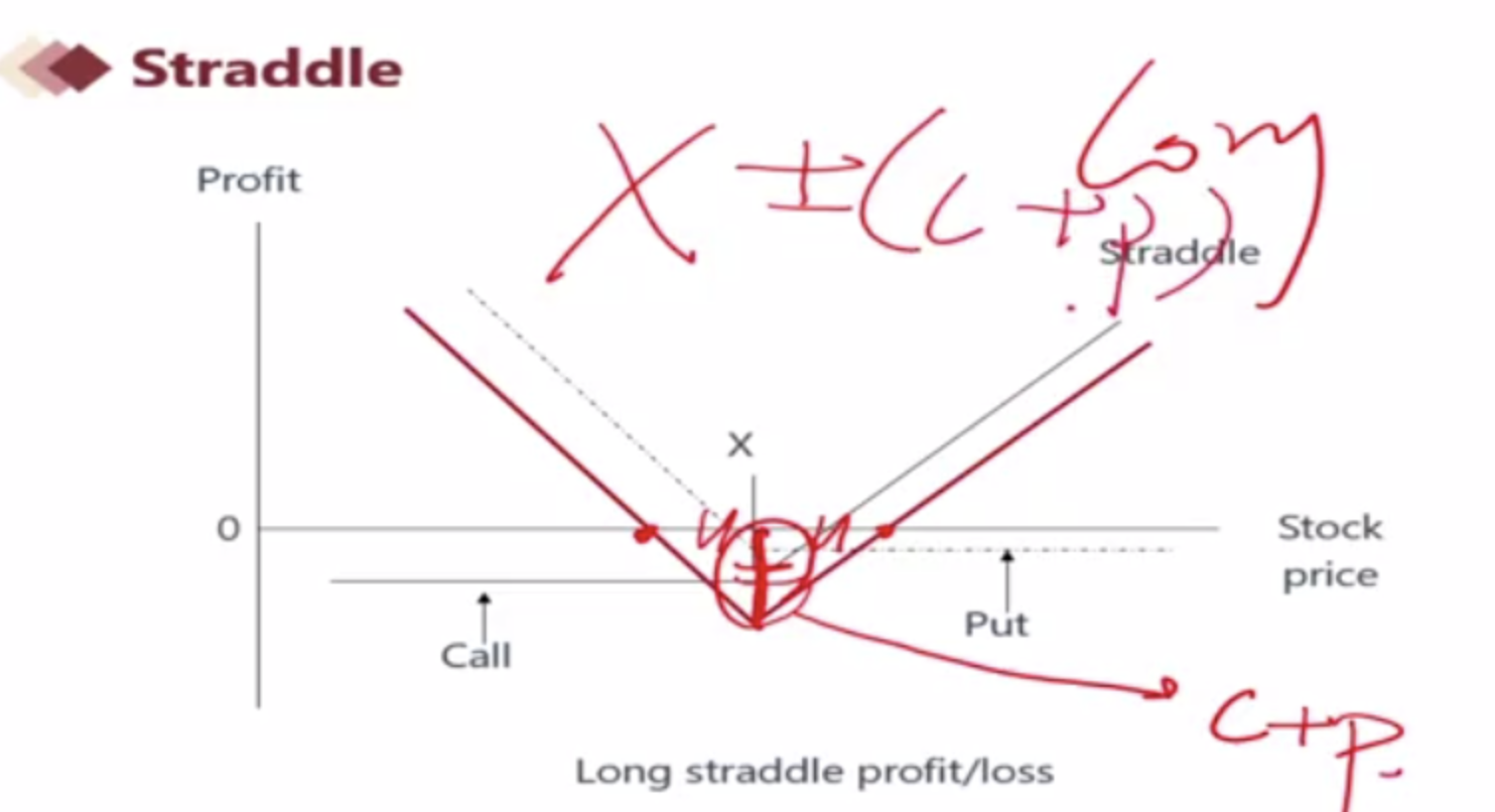
6. Straddle

同买同卖 at the same strike price. Long straddle => long volatility

• Long Straddle = + Call + Put

• Short Straddle = -Call - Put

In Sum

Sell option <=> sell volatility, long option <=> expect vol

Long call <=> long bull

Greek

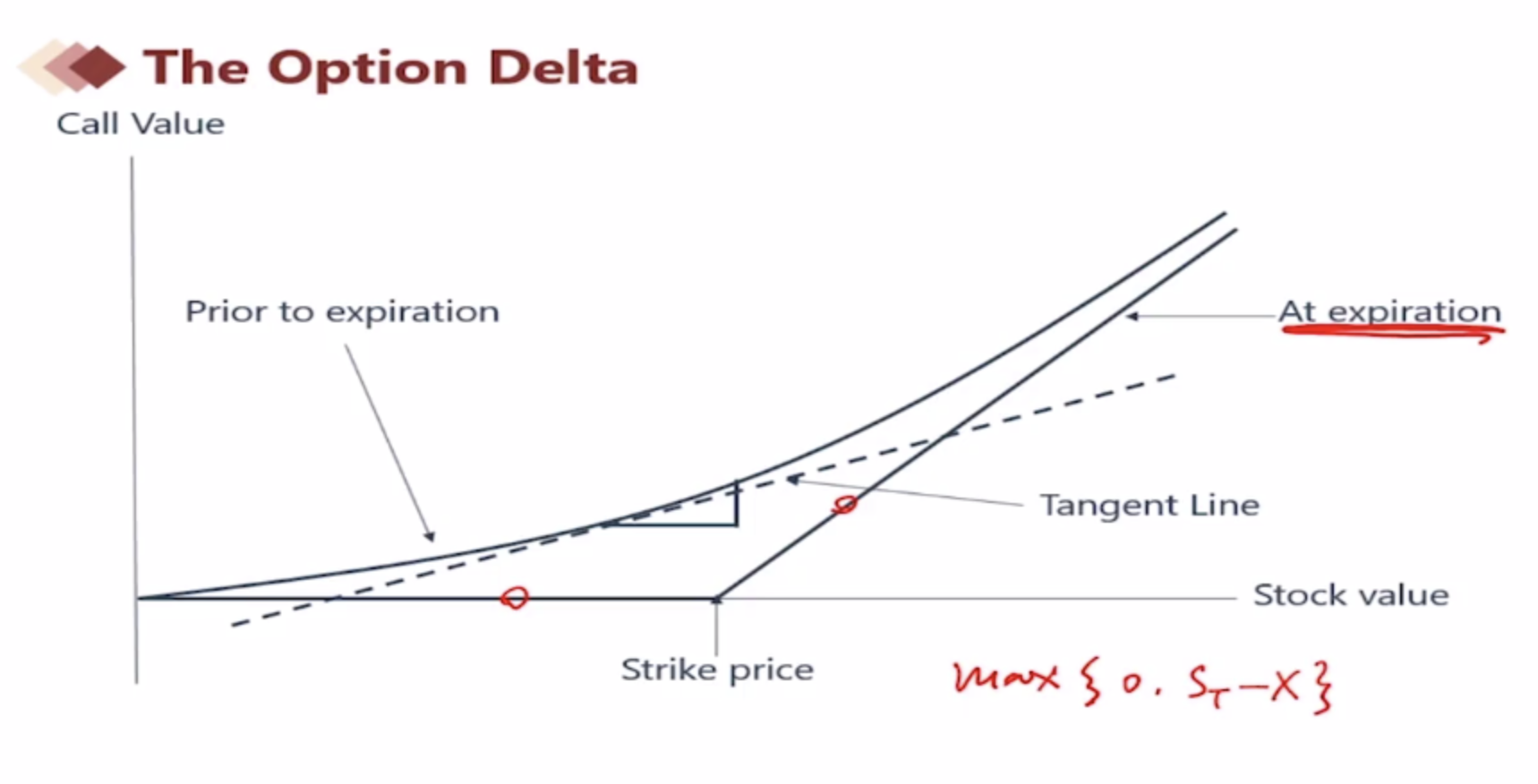
Delta of Option

Call: $\mathrm{\Delta }\in [0,1]$$\Delta \in [0,1]$

• Out-of-Money, $\mathrm{\Delta }\to 0$$\Delta \to 0$

• In-the-Money, $\mathrm{\Delta }\to 1$$\Delta \to 1$

• At-the-Money, $\mathrm{\Delta }=0.5$$\Delta = 0.5$

Put: $\mathrm{\Delta }\in [-1,0]$$\Delta \in[-1,0]$

Thus, both strategies are not delta neutral.

• Delta of Covered Call = Delta of Stock (=1) + Delta of Call ([0,1])

• Delta of Protective Put = Delta of Stock + Delta of Put ([-1,0])

• By put-call parity

  $C+\frac{K}{1+r}=p+S$$C+ \frac{K}{1+r} = p +S$

  Take derivative w.r.t. S

  ${\mathrm{\Delta }}_C+0={\mathrm{\Delta }}_P+1$$\Delta_C + 0 = \Delta_P + 1$

• By Black-Scholes Model

  $Call=S\cdot N(d_1)+K\cdot e^{-rt}\cdot N(d_2)$$Call = S\cdot N(d_1) + K\cdot e^{-rt}\cdot N(d_2)$

  ${\mathrm{\Delta }}_C=N(d_1)$$\Delta_C = N(d_1)$

Delta Hedging

Delta neutral hedging is a dynamic process

$+S-\frac{1}{\mathrm{\Delta }}C=0$$+S - \frac{1}{\Delta} C = 0$

$+\mathrm{\Delta }S-C=0$$+\Delta S - C = 0$

Gamma <- Dynamic Hedging

How delta change w.r.t. S. Lower the gamma, easily the delta hedging. Because delta is less affected.

Gamma is positive, as the curve convex.

Gamma is the maxima while option is at-the-money.

Vega <- w.r.t. volatility, Vega > 0

Theta <- w.r.t. time, Theta < 0

Rho < w.r.t. risk-free rate, >0 for call, <0 for put

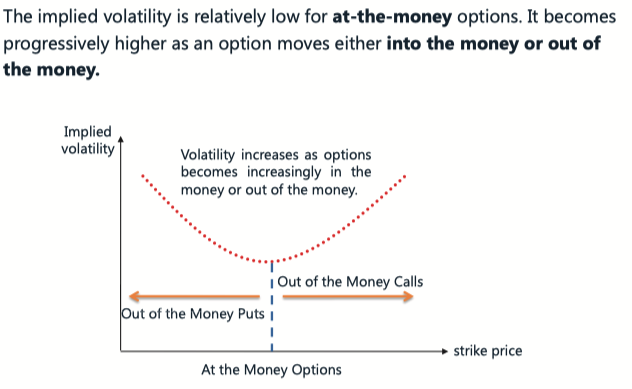
Volatility Smile

Volatility Smile and Volatility Skew Smirk

1. The Black-Sholes model assumes constant Volatility

2. Empirically for foreign currency options, when at-the-money, implied volatility is lowest

   • 结论是：OTM 的 Option 的 implied vol 更大

   

3. Equity Option, Skew (Smirk)

   • Reasons for the Smile in Equity Options

   1. Crashophbia 崩盘 market crash 可能，因为option就是用来应对危机的

   2. Leverage. As equity declines in value, company's leverage increases.

   3. Volatility Feedback Effect. 反身性，相当于 负向 accelerator

   

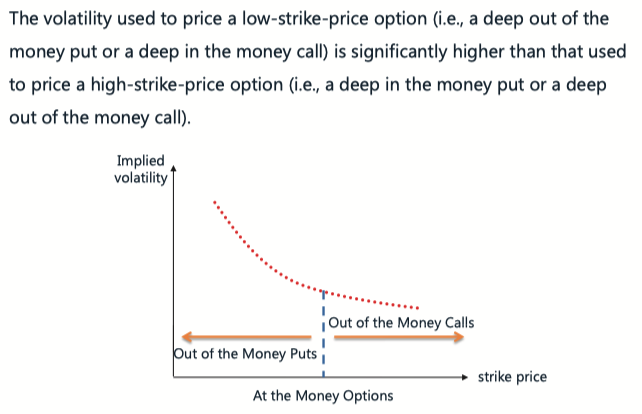
4. 同样是 OTM ，put option 价格比 call option 贵。因为，put以上三个原因。所以Put Price 大，则 implied vol for Put 大。

   OTM Put 的 vol 低, OTM Call 的 vol 高. Buy OTM Call (underpriced) and sell OTM put (overpriced)

5. Implied Volatility is compared with $\frac{K}{S_0}$$\frac{K}{S_0}$ or $\frac{K}{F_0}$$\frac{K}{F_0}$ (相当于去除量纲)

Risk Reversal

• Long Risk Reversal: 预期因为上述情况，implied volatility 被高估，那么应该

  • short put, long call 挣 put 高估和call 低估的钱

  • Then, short stocks 为了只保留 vega risks, 去除 delta risks, we then need to

• Short Risk Reversal: 反之

Term Structure of Volatility

• The term structure of volatility is often in contango, （因为期限越远，风险越高，所以upward sloped）

  (the implied volatilities for long-term options are higher)

• When market is stress, the term structure inverts.

Swaps, Forward, Futures

Manage Interest Rate Risks

Interest Rate Swap

Payer and Receiver 都指的是 对Float 的 pay / receive

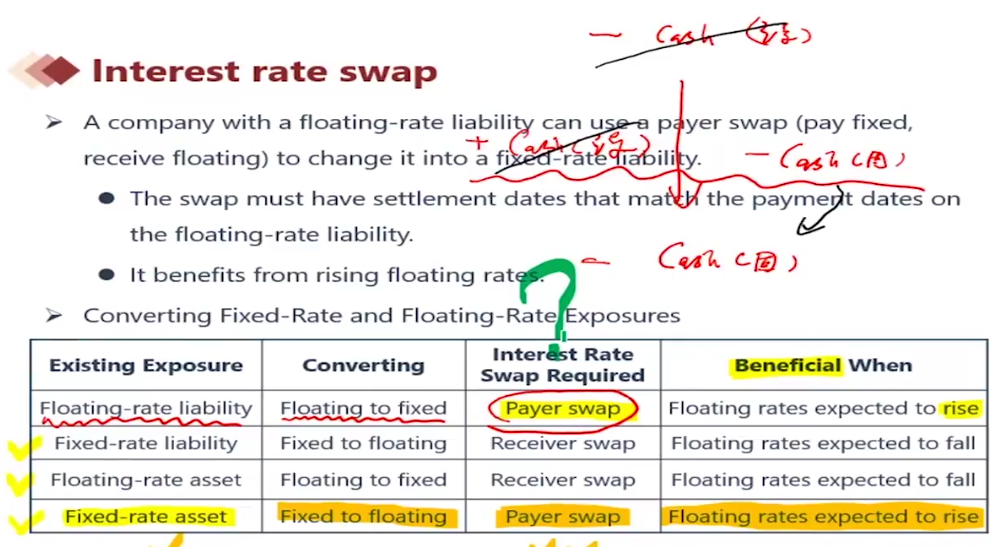
Duration of the Swap

$D_{payerFloat}=D_{Fix}-D_{Float}$$D_{payerFloat} = D_{Fix} - D_{Float}$, vice veresa

• The duration of float bond is nearly zero, thus the duration of payer float is positive, the duration of the receiver Float is negative.

• Empirically, float-rate bond duration = time period of reset . E.G. if half-year to reset, then duration = 0.5

Market Value Risks and Cash Flow Risks

• Float Bond is s.t. Cash Flow Risks 因为每一期现金流都不确定

• Fixed Bond is s.t. Market Value Risks 因为pay fixed 的部分，受 market rate 影响

• If change from float to fixed, then CF risks is neutralised and then be s.t. market value risks. Vice Versa. 如果通过swap 把float 换成了 fixed，那么从 expose cf risks 转为 expose to market value risks

Formula

$M{V}_p\times M{D}_r=M{D}_p+N_s\times M{D}_s$$MV_p \times MD_r = MD_p + N_s \times MD_s$

$D_p$$D_p$ duration, 利率变动 价格变多百分比

$D{D}_p=D_p\times V$$DD_p = D_p \times V$ dollar duration, 利率变动，价格变动多少元

$D_p=w_1{D}_1+w_2{D}_2$$D_p = w_1 D_1 + w_2 D_2$

$D{D}_p=D{D}_1+D{D}_2$$DD_p = DD_1 + DD_2$, coz $D_p=w_1{D}_1+w_2{D}_2$$D_p = w_1 D_1 + w_2 D_2$ multiply $V_p$$V_p$ from the both sides,

$D_p{V}_p=w_1{D}_1{V}_p+w_2{D}_2{V}_p$$D_pV_p = w_1 D_1 V_p + w_2 D_2 V_p$

$D{D}_p=V_1{D}_1+V_2{D}_2$$DD_p = V_1D_1 + V_2 D_2$, coz $V_1=w_1{V}_p$$V_1 = w_1 V_p$

$D{D}_p=D{D}_1+D{D}_2$$DD_p = DD_1 + DD_2$

如何通过 swap 达到目标 Durations.

$D_{original}+\underset{InterestRateSwap}{\underbrace{D_{Swap}}}=D_{target}$$D_{original} + \underbrace{D_{Swap}}_{InterestRateSwap} = D_{target}$

Solution: by Dollar Duration 能相加

$D{D}_{target}=D{D}_{original}+D{D}_{swap}$$DD_{target} = DD_{original} + DD_{swap}$ expand it

$D_{target}{V}_{target}=D_{original}{V}_{target}+D_{swap}\times N_{swap}$$D_{target} V_{target} = D_{original}V_{target} + D_{swap} \times N_{swap}$ (Notional value of the Swap)

因为在签订 swap 时， swap value = 0, 所以 $V_{target}=V_{original}+V_{swap}=V_{target}+0$$V_{target} = V_{original} + V_{swap} = V_{target} + 0$

Finally, 所以

$D_{target}{V}_{target}=D_{original}{V}_{target}+D_{Swap}{N}_{swap}$$D_{target} V_{target} = D_{original} V_{target} + D_{Swap} N_{swap}$

$N_s=\frac{D_t-D_p}{D_{swap}}\times V_p$$N_s = \frac{D_t - D_p}{D_{swap}} \times V_p$

or

$M{V}_p\times MDu{r}_p+N_s\times MDu{r}_s=M{V}_p\times MDu{r}_t$$MV_p \times MDur_p + N_s \times MDur_s = MV_p \times MDur_t$ ($M{V}_t=M{V}_p$$MV_t = MV_p$ ， 因为市场投资组合的价值 和加入swap的一样，swap在建立时value = 0)

$N_s=\frac{MDu{r}_t-MDu{r}_p}{MDu{r}_s}M{V}_p$$N_s = \frac{MDur_t - MDur_p}{MDur_s} MV_p$

• Implication:

  $D_t-D_p$$D_t - D_p$ 与 $D_{swap}$$D_{swap}$ 同向变动

Interest Rate Forwards (FRA)

Interest Rate Future (Euro-Dollar Future)

• As it is future, it's standard (not OTC as FRA).

• Guaranteed by a clearinghouse, so counterparty risk is nearly zero. 有保证金，所以交易对手方风险基本上为0

  • Cash settled

• P.S. interest rate futures are short-term, but fixed-income futures are more long time.

Euro Dollar Futures have fixed notional value and fixed term (, as it is standardised).

• Notional value: 1 million USD

• Term: 3 months

$\mathrm{\$}1,000,000\times \frac{90}{360}\times 1bp=\mathrm{\$}25$$\$1,000,000 \times \frac{90}{360}\times 1bp = \$25$

Fixed-Income Futures

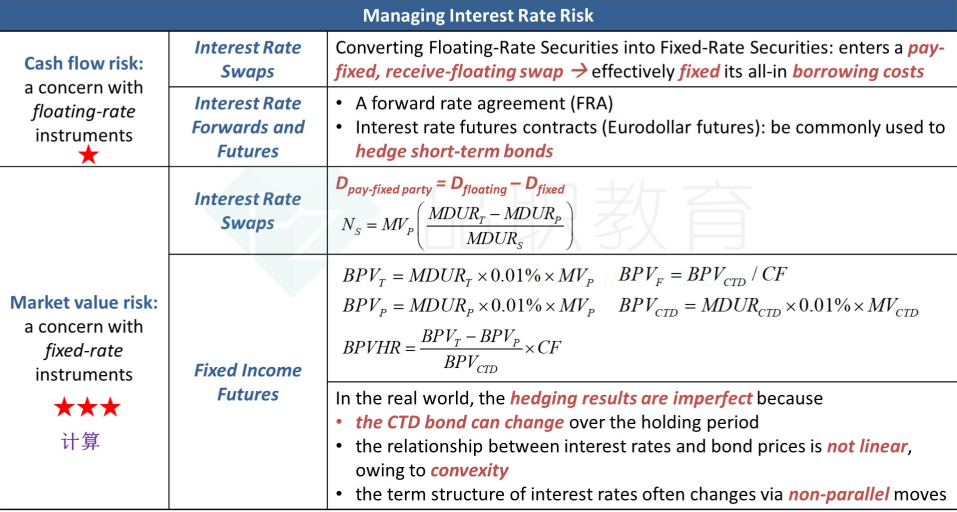
Treasury-bond is the underlying asset, we do not use corporate bond as there is less liquidity and more credit risks.

Delivery

There is a portfolio of T-bonds/bills for settlement. As the Fixed-Income Futures are standarised, they are traded in the exchange, and are settled daily. 标准化的future，有一个basket，交易所交割，可以 cash 可以实物交割

• the Short side has a dilivery option to choose which bond to deliver 意味着short方可以决定deliver哪个，所以有CF转换 basket里的，所以有CTD

Basket 中的 bonds 有 CF (conversion factor) 用来调节 Basket 中不同 bonds 不同期限的rates等带来的差额, 和 Accured Interest 的差别

Clean + Accured Int = Dirty

$Clean=\text{Quoted Futures Settlement Priec}\times CF$$Clean = \text{Quoted Futures Settlement Priec} \times CF$

$Dirty=QuotedPrice\times CF+AI$$Dirty = QuotedPrice \times CF + AI$

CTD

Futures contract Sell has the right to choose the CTD (cheapest-to-delivered)

$CTD=$$CTD =$$QuotedPrice\times CF$$Quoted Price \times CF$

Market Yield v.s. Notional Yield

• if market yield > notional yield, then long duration bond is likely to be CTD (最合适用来交割的)

  • 因为 market rate 大的 ，duration 长 的折价多

  • 

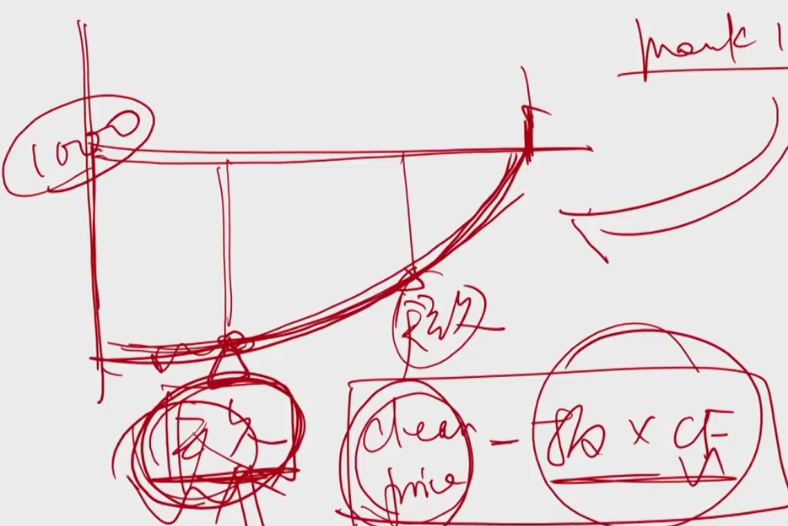
  • 如图，久期长的离 expired date 远，折价越多。但是这只是clean price 方面，还未考虑 Accured Interest

• if market yield < notional yield 的， 短久期的 可能为 CTD （更便宜，适合交割）原因见上图，把图沿 y-axis 对称

Basis Trading

Basis = S - F , in alternatives 为空头方的交割成本，basis converge to zero with time

$Basis=S-F\times CF$$Basis = S - F \times CF$

• if basis is positive, sell the basis , ( long the future and short the bond) 因为 Basis converges to zero, 所以如果 basis 正，那么S会变小，F会变大 使basis趋近于0

• if the basis is negative, buy the basis, ( long the bond and short the future)

Fixed-Income Future Hedging

担心 interest rate 上涨， 带来 T-bond Price 下跌，同时 Fixed-Income Future 价格下跌，所以 Short Futures

Basis Point Value for Bonds ( BPV

• $BP{V}_{CTD}=MDu{r}_{CTD}\times M{V}_{CTD}\times 0.01\mathrm{\%}$$BPV_{CTD} = MDur_{CTD} \times MV_{CTD} \times 0.01\%$

  • $M{V}_{CTD}=(CTDQuotedPrice)\times Future$$MV_{CTD} = (CTD\ QuotedPrice) \times Future$

• $BP{V}_F=MDu{r}_F\times Pric{e}_F\times 0.01\mathrm{\%}$$BPV_F = MDur_F \times Price_F \times 0.01\%$

P.S. recall, irrelevent with the other content

• $MaculyDuration$$Maculy Duration$ 为时间（年）

• $MDu{r}_F$$MDur_F$ 修正久期: 1% 利率变动 => 投资期货合约 收益变动% ($MDur$$MDur$)

• $D{D}_F$$DD_F$ 美元久期: 1% 利率变动 => 收益变动 amount $，BPV 类比 DD，为value

Hedge Ratio <- Number of Future Contract

$\mathrm{\Delta }P=HR\times \mathrm{\Delta }F$$\Delta P = HR \times \Delta F$ => $HR=\frac{\mathrm{\Delta }P}{\mathrm{\Delta }F}$$HR = \frac{\Delta P}{\Delta F }$

Similarly

• Basis Point Value Hedge Ratio (BPVHR) 即为 N

  • $BPVHR=-\frac{BP{V}_P}{BP{V}_F}$$BPVHR = - \frac{BPV_P}{BPV_F}$

  • $BP{V}_F\times CF=BP{V}_{CTD}$$BPV_F \times CF= BPV_{CTD}$

  • => $BPVHR=-\frac{BP{V}_P}{BP{V}_{CTD}}\times CF$$BPVHR = - \frac{BPV_P}{BPV_{CTD} } \times CF$

  • The number of future to sell to fully hedge the portfolio is 345 future contracts

负号不能丢，表示 hedge 与 underlying 的变动是相反的

Adjust Portfolio Duration

$BP{V}_{Portfolio}+N\times BP{V}_{Future}=BP{V}_{Target}$$BPV_{Portfolio} + N\times BPV_{Future} = BPV_{Target}$

通过加入 $N\times BP{V}_{Future}$$N\times BPV_{Future}$ 项，调将 portfolio 的久期调成 target 的数额

N is named BPVHR，根据上式，解出 BPVHR

$BPVHR=\frac{BP{V}_T-BP{V}_P}{BP{V}_F}$$BPVHR = \frac{BPV_T - BPV_P}{BPV_F}$

• $BP{V}_T=M{V}_P\times D_{Target}\times 1bp$$BPV_T = MV_P \times D_{Target} \times 1bp$

• $BP{V}_P=M{V}_P\times D_{Portfolio}\times 1bp$$BPV_P = MV_P \times D_{Portfolio} \times 1bp$

• $BP{V}_F\times CF=BP{V}_{CTD}$$BPV_F \times CF= BPV_{CTD}$ (Accured Interest is ignored just now)

• Finally, $BPVHR=\frac{BP{V}_T-BP{V}_P}{BP{V}_{CTD}}\times CF$$BPVHR = \frac{BPV_T - BPV_P}{BPV_{CTD}}\times CF$

Manage Equity Risk

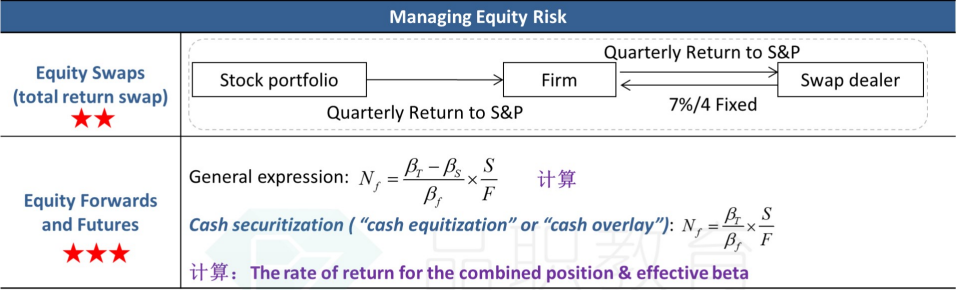
管理 Equity Risks 的方法 (1) Swap (2) Future and Forward <- adjust target portfolio beta & cash equitisation

Equity Swap

• fixed rate <-> equity return

• float rate <-> equity return

• equity return <-> another equity return (high risks)

returns are from

1. a single stock

2. a basket equity (ETF)

3. an equity index

Futures

Adjust Beta

Future price is quoted as: $F=\underset{QuoteFuturePrice}{\underbrace{f}}\times Multiplier$$F = \underbrace{f}_{QuoteFuturePrice} \times Multiplier$ ($f$$f$ is %, multiplier convert the $F$$F$ into $ amount)

$N_f=\frac{{\beta }_T-{\beta }_p}{{\beta }_f}\frac{M{V}_p}{F}$$N_f = \frac{\beta_T-\beta_p}{\beta_f} \frac{MV_p}{F}$

$N_f=\frac{{\beta }_T-{\beta }_p}{{\beta }_f}\times \frac{M{V}_p}{f\times Multiplier}$$N_f = \frac{\beta_T-\beta_p}{\beta_f} \times \frac{MV_p}{f\times Multiplier}$

${\beta }_p\times M{V}_p+\mathrm{\#}\times {\beta }_f\times \underset{F(\mathrm{\$}amount)}{\underbrace{(f\times Multiplier)}}={\beta }_T\times M{V}_p$$\beta_p \times MV_p+ \# \times \beta_f \times \underbrace{(f\times Multiplier)}_{F (\$ amount)} = \beta_T \times MV_p$

$\mathrm{\#}=N_f=\frac{{\beta }_T\times M{V}_p-{\beta }_{p}M{V}_p}{{\beta }_f\times f\times Multiplier}=\frac{{\beta }_T-{\beta }_p}{{\beta }_f}\frac{M{V}_p}{f\times Multiplier}$$\# =N_f= \frac{\beta_T \times MV_p - \beta_p MV_p}{\beta_f \times f \times Multiplier} = \frac{\beta_T -\beta_p}{\beta_f}\frac{MV_p}{f\times Multiplier}$

Or $=\frac{{\beta }_T-{\beta }_p}{{\beta }_f}\frac{M{V}_p}{F}$$= \frac{\beta_T -\beta_p}{\beta_f}\frac{MV_p}{F}$

$F\iff f\times Multiplier$$F \Leftrightarrow f \times Multiplier$ are $ amount

Cash Equilisation

make ${\beta }_p$$\beta_p$ or ${\beta }_T$$\beta_T$ as "0".

• Synthetic Risk-free Asset ${\beta }_T=0$$\beta_T=0$

  $N_f=\frac{0-{\beta }_p}{{\beta }_f}\frac{M{V}_p}{f\times Multiplier}$$N_f = \frac{0 - \beta_p}{\beta_f}\frac{MV_p}{f\times Multiplier}$

• Synthetic Equity ${\beta }_p=0$$\beta_p = 0$

  $N_f=\frac{{\beta }_T-0}{{\beta }_f}\frac{M{V}_p}{f\times Multiplier}$$N_f = \frac{\beta_T -0}{\beta_f}\frac{MV_p}{f\times Multiplier}$

Using Derivatives to Alter Asset Allocation

如 Fund has 33.33% Bonds + 66.67% Equity， 想调整为 30% Bonds + 70% Equity。因为若fund很大，直接抛售等买卖会带来资产价格大幅变动。

为了避免价格波动，我们不直接买卖资产，而是买卖对应的 derivatives (futures and forwards)，因为这样可以最小化对市场价格的影响

通过 Cash Position make $\beta =0,forStocks$$\beta = 0, for\ Stocks$, $BPV=0,forBonds$$BPV = 0, for\ Bonds$

所以此时，并不是直接 Sell bond，而是 make $BP{V}_T=0$$BPV_T=0$

不是直接 buy equity，而是 make $\beta =0$$\beta=0$

Manage Currency Risks

本国US investor 要买 EU bond。进入Cross-currency Swap. （现金流结构相当于在期初 花USD 买了 USD bond，收EUR，发行EUR bond）

1. 在inception期初 换本金 付出 USD principal 收到 EUR principal

2. 在 periodic 期中， pay EUR interest， 收到 USD interest （有 basis）一般dealer在哪国就需要哪国的basis。如本国US，那么dealer也在US，那么investor收到的 USD interim interest 就会有 basis扣除，即为 dealer 挣的钱

3. 在期末 换回本金。收到 USD，付出 EUR

• P.S. 如果美元涨价，那么外国人要付basis给本国

• In this case, US investor pays USD and receives EUR, if the USD appreciates the US investor needs to pay more interest of USD, but why the answer is "the US investor will most likely increase the periodic net interest she receives in US dollars." the US investor pays USD!!!

Cross-currency basis: additional cost of borrowing dollar (most currencies show a negative basis against dollar) 即美元有加点

$\frac{F}{S}=\frac{1+r_f}{1+r_d\pm (basis)}$$\frac{F}{S} = \frac{1+r_f}{1+r_d \pm(basis)}$

if USD (domestic) is strong, then receive basis

• Sample Text:

  Cross currency basis is a measure of dollar shortage in the market. Whenever there’s a higher demand for the dollar, the counterparty lending the dollar will ask for a price premium. It is this amount which is referred to as the “cross currency basis”. The more negative the basis becomes, the more severe the shortage.

  For a European investor looking to take a loan (borrow) from a domestic bank (EUR) and enter a EUR/USD currency swap, if the basis is (-) then there is a Dollar shortage, and European investor will have to pay additional basis.

  For dollar-funded investors, negative basis can work in their favor when they hedge currency exposures. In order to hedge foreign currency exposure, the dollar-funded investors lend out dollar today and receive it back in the future, earning additional cross currency basis spread on top of the yield of their foreign investments.

Cross-Currency Basis Swap 期初还两个币种的本，期末换回来

Swap the notional principals, 本金可以在beginning换，在ending换回来 but periodic interest payment could not be netted 期间的利息不换

Synthetic Borrowing 不换本金

No exchange the principals. Instead,

exchange CF in the future at fixed exchange rate

The amount of exchanged are based on the Exchange Rate and Interest Rate

Currency Forward and Futures

$HR=\frac{\text{Amount of Currency to be Exchanged}}{\text{Future Contract Size}}$$HR = \frac{\text{Amount of Currency to be Exchanged}}{\text{Future Contract Size}}$

Buy EUR/USD 相当于买USD

Sell EUR/USD 相当于卖USD

Manage Volatility Risks

• Volatility Derivatives

  1. VIX Futures

  2. VIX Options

  3. Volatility index

• Variance Swap

VIX Futures

VIX and Equity returns are mostly negative correlated

P.S. Cost of Carry model does not work on VIX $F=SX(1+r_f{)}^T-CB+CC$$F = S X(1+r_f)^T - CB + CC$, because VIX spot is not able to be invested (VIX is an index, is calculated)

• 如果是 Contango, 横坐标 term，纵坐标 price，向上倾斜。这意味着：随着期限减少（向 term = 0），价格会降低。

  • 这意味着，在 roll VIX future 时，如以100买 t=10，卖90 在t=9。再roll，卖80在t=8，etc。每次roll的价格都会降低。所以contango的情况会亏 price

  • $RollYield=\frac{F-S}{S}$$RollYield = \frac{F-S}{S}$

• 如果是 backwards，在 roll的时候，price会提升，可以挣 price 提升的钱。

Variance Swap

Payoff of Variance Swaps is based on Variance rather than Volatility (s.d.).

No Exchange of Notional Principal and No interim Settlement periods

• Variance Stike (Implied Volatiltiy), $K^2$$K^2$: the implied vol at the beginning

  • $Strike=K,\text{and }variancestrike=K^2$$Strike = K , \text{and } variance \ strike = K^2$

• Realised Variance, ${\sigma }^2$$\sigma^2$: Actual Vol over the life of the swap

Swap 的双方为 ${\sigma }^2$$\sigma^2$ and $K^2$$K^2$. 如果市场上实际的 variance, ${\sigma }^2>K^2$$\sigma^2>K^2$ the strike price squared.

那么 每份swap 的payoff 是 ${\sigma }^2-K^2$$\sigma^2 - K^2$ 相当于用$K^2$$K^2$买${\sigma }^2$$\sigma^2$.

整个 swap 的 payoff 是，即 settlement amount = $N_{variance}\times ({\sigma }^2-K^2)$$N_{variance}\times (\sigma^2 - K^2)$

• Vega Notional 的定义: $N_{vega}=\frac{Gain-Loss}{2}$$N_{vega} = \frac{Gain - Loss}{2}$ 因为loss是负数，我们要absolute amount所以用 -loss 调整为正的

  • Gain: $(K+1{)}^2\times N_{variance}$$(K+1)^2\times N_{variance}$

  • Loss: $(K-1{)}^2\times N_{variance}$$(K-1)^2\times N_{variance}$

• So, $N_{vega}=\frac{4K}{2}=2K\times N_{variance}$$N_{vega} = \frac{4K}{2}=2K\times N_{variance}$

• $N_{variance}=\frac{N_{vega}}{2K}$$N_{variance} = \frac{N_{vega}}{2K}$

• Settlement Amount (long): $=\frac{N_{vega}}{2K}\times ({\sigma }^2-K^2)$$=\frac{N_{vega}}{2K}\times (\sigma^2-K^2)$

• $veganotional$$vega \ notional$ 是指实际中 quote Variance Swap 的报价，题目会给的数值，让我们算 variance notional

P.S. the payoff of variance swap is convex 即 var 增大带来的 payoff 提升 > 比 var 减少带来的 payoff 减少。投资者喜欢

Mark-to-Market (MtM) Value of Variance Swap

在swap中间某一点 Variance Swap 的 Value （既然是value，就要折现到 t=0)

盯市，因为 swap 在 beginning is made to be zero value，但是随着时间和市场变化（${\sigma }^2\text{and}{K}^2$$\sigma^2 \ \text{and}\ K^2$ 变化） swap开始有价值

MtM 指在 t 时间估计出来的，对到期日 var 的估计（加权平均）

$ExpectedVariancetoMaturity=({\sigma }_t^2\times \frac{t}{T})+(K_{T-t}^2\times \frac{T-t}{T})$$Expected \ Variance\ to \ Maturity = (\sigma^2_t \times \frac{t}{T}) + (K^2_{T-t} \times \frac{T-t}{T})$

$weight{s}_1=t/T,weigh{t}_2=(T-t)/T$$weights_1 = t / T, weight_2 = (T-t)/T$

• ${\sigma }_t^2$$\sigma_t^2$ 在 t 时间点已实现的 variance

• $K_{T-t}^2$$K_{T-t}^2$ 在 t 时间点 开启一份预期 T 到期的 Strike Price of Swap，为 implied variance, = fair strike of a new (T-t) variance swap

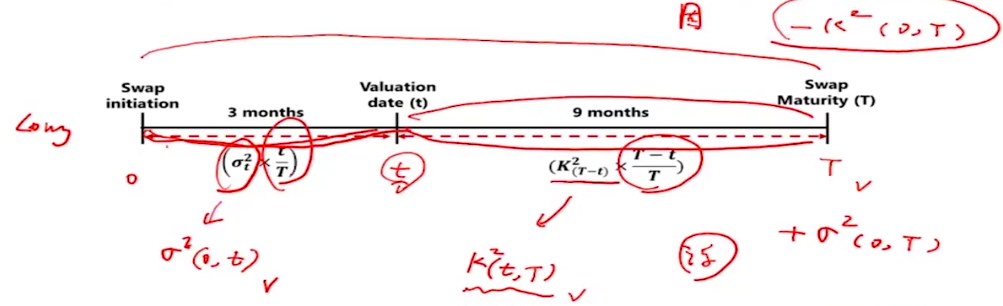
• then 用expected var to maturity - Strike, 得到T时点Swap的payoff

  $({\sigma }_t^2\times \frac{t}{T})+(K_{T-t}^2\times \frac{T-t}{T})-Strik{e}_T^2$$(\sigma^2_t \times \frac{t}{T}) + (K^2_{T-t} \times \frac{T-t}{T}) - Strike_T^2$

• 把 T 时点的 payoff 折现即为 现在的 value, 是 从 T 折现到 t，单利，所以折现为 T-t

  $\frac{({\sigma }_t^2\times \frac{t}{T})+(K_{T-t}^2\times \frac{T-t}{T})-Strik{e}_T^2}{1+r\times \frac{T-t}{T}}$$\frac{(\sigma^2_t \times \frac{t}{T}) + (K^2_{T-t} \times \frac{T-t}{T}) - Strike_T^2}{1+r\times\frac{T-t}{T}}$

Inferring Market Expectation

• Fed Funds Futures

  • $\text{Fed Funds Future Contract Price}=100-ExpectedFFErate$$\text{Fed Funds Future Contract Price} = 100 - Expected FFE\ rate$

  • future 是市场预期报价的，所以反映了市场的预期

  • Eurdollar Futures

    • Dollar deposited in the outside of US

    • Quoted Price = 100 - Future Interest Rate

  • Federal Fund Rate: overnight rate deposite rate by the Fed

  • Federal Fund Target Rate, set by FOMC meetings

• Expected Probability

  假设利率在区间内服从均匀分布，测算 市场预期的rate 即 future，与如果FOMC 真正调整了的 Price 的差距

  $\frac{\text{Expected FFE}-\text{CurrentFFR}}{\text{FFR.Hike/Down}-\text{Current FFR}}$$\frac{\text{Expected FFE} - \text{CurrentFFR} }{\text{FFR.Hike/Down} - \text{Current FFR}}$

  $\text{FFR.Hike/Down}=\text{Current FFR}\pm 25bp$$\text{FFR.Hike/Down} = \text{Current FFR} \pm25bp$

  所以，分母一般一定为 25bp

Currency Management

Currency Swap

Mark-to-Market Value

MtM 指在 currency swap 存续期，swap 的value （因为 initial 的时候 value = 0）

FX Swap 本质上是 forward 借新还旧

• Similar to currency swaps, FX swaps involve an exchange of principal amounts in different currencies at swap initiation that is reversed at swap maturity. 与 currency swap 相同的是 在 initiation 和 expire

• Unlike currency swaps, FX swaps have no interim interest payments不同点是 不互换中期的

Effects of Currency on Portfolio

• Foreign Currency Return, $R_{FC}$$R_{FC}$ 指的是 资产价格的变动 foreign asset @ foreign currency 的return

• Local Currency Return, $R_{FX}$$R_{FX}$ 指的是 the percentage of foreign currency agaisnt the domestic currency 指的是汇率的变动

• Domestic Currency Return , $R_{DC}$$R_{DC}$ 指的是 rate of return stated in domestic currency term

Returns

RHS 在外国投资的收益 * 汇率变动的收益

$1+R_{DC}=(1+R_{FC})(1+R_{FX})$$1+ R_{DC} = (1+R_{FC})(1+R_{FX})$

• $R_{FX}$$R_{FX}$ is defined as the percentage change in the foreign currency against the domestic currency. $R_{FX}$$R_{FX}$ is in the directly quoted exchange rate.

• Because market quotes are not always in direct terms, analysts will need to convert to direct quotes before calculating percentage changes. 如果不是 direct quote，要先调整为 direct quote 在算 R_{fx}

in a portfolio

$1+R_{DC}=\sum _i^{n}w(1+R_{FC})(1+R_{FX})$$1+R_{DC} = \sum_i^n w(1+R_{FC})(1+R_{FX})$

$R_{DC}=\sum _i^{n}w(1+R_{FC})(1+R_{FX})-1$$R_{DC} = \sum_i^n w(1+R_{FC})(1+R_{FX}) - 1$

Variance

$Var(R_{DC})=Var((1+R_{FC})(1+R_{FX})-1)$$Var(R_{DC}) = Var\bigg((1+R_{FC})(1+R_{FX}) - 1\bigg)$

$R_{FC}\times R_{F}X$$R_{FC}\times R_FX$ is $o(R)$$o(R)$, so ignore it

${\sigma }_{R_{DC}}^2\approx {\sigma }_{R_{FC}}^2+{\sigma }_{R_{FX}}^2+2{\sigma }_{R_{FC}}{\sigma }_{R_{FX}}\times Corr$$\sigma^2_{R_{DC}}\approx \sigma^2_{R_{FC}} + \sigma^2_{R_{FX}} + 2\sigma_{R_{FC}}\sigma_{R_{FX}}\times Corr$

Other Considerations

• if Correlated is low, $Corr\downarrow$$Corr \downarrow$, then ${\sigma }_{R_{DC}}^2\downarrow$$\sigma^2_{R_{DC}} \downarrow$, Implication 如果外汇和资产负相关，那么 risk 低

• if there is not exchange rate risks, of says if there the exchange rate pegged, then $R_{FX}=0$$R_{FX}=0$, then ${\sigma }_{R_{DC}}^2\approx {\sigma }_{R_{FC}}^2$$\sigma^2_{R_{DC}} \approx \sigma^2_{R_{FC}}$

• if $R_{FC}$$R_{FC}$ is a risk-free return, then $R_{FX}=r_f=Constant$$R_{FX} =r_f = Constant$ is a constant

  $Var(R_{DC})=Var((1+R_{FC})(1+R_{FX})-1)$$Var(R_{DC}) = Var\bigg((1+R_{FC})(1+R_{FX}) - 1\bigg)$

  $Var(R_{DC})=Var((1+r_f)(1+R_{FX})-1)=Var((1+r_f)R_{FX})$$Var(R_{DC}) = Var\bigg((1+r_f)(1+R_{FX}) - 1\bigg) = Var\bigg((1+r_f)R_{FX} \bigg)$

  $\sigma (R_{DC})=\sigma ((1+r_f)R_{FX})$$\sigma (R_{DC}) = \sigma\bigg((1+r_f)R_{FX} \bigg)$

Strategic Currency Management

• Formulate IPS: general objectives, risk tolerance, time horizon, ongoing income and liquidity, benchmark (rebalance周期)

• Choice of Currency Exposures: 要对冲多少

• 1. Diversification Consideration

     1. in the long run, it would not matter if the portfolio was hedged or not

     2. if $R_{FC}$$R_{FC}$ and $R_{DC}$$R_{DC}$ are negatively correlated, then ${\sigma }_{R_{DC}}$$\sigma_{R_{DC}}$ is small, so less exposure is enough

     3. Correlation ${\rho }_{R_{FX},R_{FC}}^{Bond}>{\rho }_{R_{FX},R_{FC}}^{Equity}$$\rho_{R_{FX},R_{FC}}^{Bond} > \rho_{R_{FX},R_{FC}}^{Equity}$. This assertion makes intuitive sense: both bonds and currencies react strongly to movements in interest rates, whereas equities respond more to expected earnings. So, less hedge on ${\rho }_{R_{FX},R_{FC}}^{Equity}$$\rho_{R_{FX},R_{FC}}^{Equity}$ because low corr low risks, more hedge on ${\rho }_{R_{FX},R_{FC}}^{Bond}$$\rho_{R_{FX},R_{FC}}^{Bond}$ because more corr more risks

  2. Cost Consideration

     1. trading expense while rebalance frequency is high

     2. if options are OTM (out of the moeny), then less expense

     3. As Forwards need to be "rolled" and produce cost, we use FX swap.

        however, as rolling hedges will generate cash inflows and outflows, and thus more volatiltity on cash account

     4. Opportunity of the hedge. (rule of the thumb, 50% hedge ratio). Hedge the larger advese moments, ignore the minor.

  3. Choice of Currency Management Strategies / Hedging

     • Optimal hedging decisions require balancing the benefits of hedging against the costs of hedging.

     • Hedging Costs are from (1) trading cost (2) opportunity cost

     1. Passive Hedge, 100% hedge with benchmark portfolio used to evaluate performance

     2. Discretionary Hedge, with limits. 为了降风险

        • The primary duty of the discretionary hedger is to protect the portfolio from currency risk.

     3. Active Currency Management, more active management 为了提升收益

     4. 0% is assume the market is efficient that speculation is useless.

     5. Currency Overlay， 0% hedge 有专员负责 trade and bargin with the FX, speculate

        • If internal resources for active management are lacking, the fund manager would outsource currency exposure management to a sub-advisor that specializes in foreign exchange management. This approach would allow the fund manager of Portfolio A to separate the currency hedging function (currency beta), which can be done effectively internally, and the active currency management function (currency alpha) which can be managed externally by a foreign currency specialist. 外包给专门做外汇交易的人做，可以挣 currency beta 和 currency aloha

  4. Formulate a Currency Mgt. Program

     The situation we need bias toward more-fully hedged currency mgt programs 需要更多对冲的情况

     1. have a short term objective

     2. Risk averse

     3. Immediate Income/Liqudity needs

     4. Fixed-income assets are held as ${\rho }_{R_{FX},R_{FC}}^{Bond}$$\rho_{R_{FX},R_{FC}}^{Bond}$ is higher

     5. hedge program is cheap

     6. financial mkt is volatile or risky

     7. Skeptical the benefical owners 客户怀疑 / management oversight active mgt 监管控制 active currency mgt

Active Currency Approach

• Technical Analysis: Market technicians believe that in a liquid, freely-traded market the historical price data already incorporates all relevant information on future price movements. Technicians believe that it is not necessary to look outside the market at data like the current account deficit, inflation and interest rates because current exchange rates already reflect the market consensus view on how these factors will affect future exchange rates.

• Carry Trade: . This strategy is implemented by borrowing in low-yield currencies (USD at 1%) and investing in high-yield currencies (INR at 8%).

• Economic Fundamentals: This approach assumes that, in free markets, exchange rates are determined by logical economic relationships that can be modeled. A fundamentals-based approach estimates the “fair value” of the currency, with the expectation that observed spot rates will converge to long-run equilibrium values described by parity conditions.

Volatility Trader

Tactical Currency Management

• Domestic Currency would appreciate if

  1. Long-run equilibrium real exchange rate increases

  2. Real and nominal interest rate increase

  3. Expected foreign inflation increase (so foreign currency depreciates)

  4. Foreign risks premium increase

Technical Analysis

• Golden Cross, Dead Cross

• Overbought or Oversold

• Support and Resistance levels cluster

  • Price gets sticky, gov control in the background. But, Once certain price points breached, the price would accelerate.

Carry Trade

UIP & CIP

UIP states 如果F国的利率高，那么投资者会把钱存入F国挣高收益率。但是F国远期的汇率一定会降，去保证UIP holds

In sum, country with high rate of return would have forward discount 远期比现在低 , we invest in high return one, (, equivalent to invest in forward discount one)

Carry Trade can make money iff the UIP is violated 只有违背 UIP 才有 carry trade 赚钱的机会

$1+r_d=\frac{1+r_f}{S}F$$1+r_d = \frac{1+r_f}{S}F$ , where $F$$F$ or $S$$S$ is $(\frac{d}{f})$$(\frac{d}{f})$. Base Currency is the foreign currency, 我们主要以foreign currency 为参考，if F 提升，意味着 d > f，意味着外币升值

$\frac{F}{S}=\frac{1+r_d}{1+r_f}$$\frac{F}{S} = \frac{1+r_d}{1+r_f}$

• on a longer-term average, the return on an unhedged foreign-currency asset investment will be the same as a domestic-currency investment.

• The yield spread advantage for the high-yielding currency (the right side of the equation) will, on average, be matched by the depreciation of the high-yield currency.

Arbitrage

if $\frac{F}{S}>\frac{1+r_d}{1+r_f}$$\frac{F}{S} > \frac{1+r_d}{1+r_f}$, $\frac{F}{S}(1+r_f)>1+r_d$$\frac{F}{S} ({1+r_f})> {1+r_d}$, then borrow $r_d$$r_d$ as its is low cost, and invest in $f$$f$. The arbitrage return would be $\frac{F}{S}(1+r_f)-(1+r_d)$$\frac{F}{S} ({1+r_f}) - ({1+r_d})$

if $\frac{F}{S}<\frac{1+r_d}{1+r_f}$$\frac{F}{S} < \frac{1+r_d}{1+r_f}$, $\frac{S}{F}(1+r_d)>1+r_f$$\frac{S}{F} ({1+r_d})> {1+r_f}$, then borrow $r_f$$r_f$ as its is low cost, and invest in $d$$d$, then the arbitarge return would be $\frac{S}{F}(1+r_d)-(1+r_f)$$\frac{S}{F} ({1+r_d}) -( {1+r_f})$,

remember always let F/S or S/F be in the larger side.

Returns from Carry Trade

However, in reality, high-yield countries often see their currencies appreciate, not depreciate, for extended periods of time. Reasoning:

1. Capital Inflow

2. yield difference

Forward Rate Bias & Carry Trade

Carry Trade 的逻辑，借入 $r$$r$ 小的，投资 $r$$r$ 大的，挣$\mathrm{\Delta }r$$\Delta r$

• Forward Bias: buying currencies selling at a forward discount ($F<S$$F<S$, 即高利率货币), and selling currencies trading at a forward premium.

  $F/S=\frac{1+r_d}{1+r_f}$$F/S = \frac{1+r_d}{1+r_f}$ (, where (d/f) the base is f, , if $r_f>r_d$$r_f > r_d$, then <=> $F<S$$F<S$, that is forward discount, then borrow $d$$d$ and invest in $f$$f$. So, if forward discount, then invest in the base $f$$f$.

• Connection between Carry Trade & Forward Bias. Forward Rate Bias, 低利率的货币，远期是溢价的，所以卖。高利率货币，远期折价，所以买

Volatility Trading

Straddle <- bet on volatility

By Delta Hedging, we can get a delta-neutral position. Straddle is a long call and a long put ATM.

Straddle is delta Neutral, because it is symmetric at the current stock price.

Strangle

Long Call and long put OTM, but as options are OTM, so lower premium 期权费便宜.

The Green Curve is Straddle, Yellow Curve is Strangle, in the below figure.

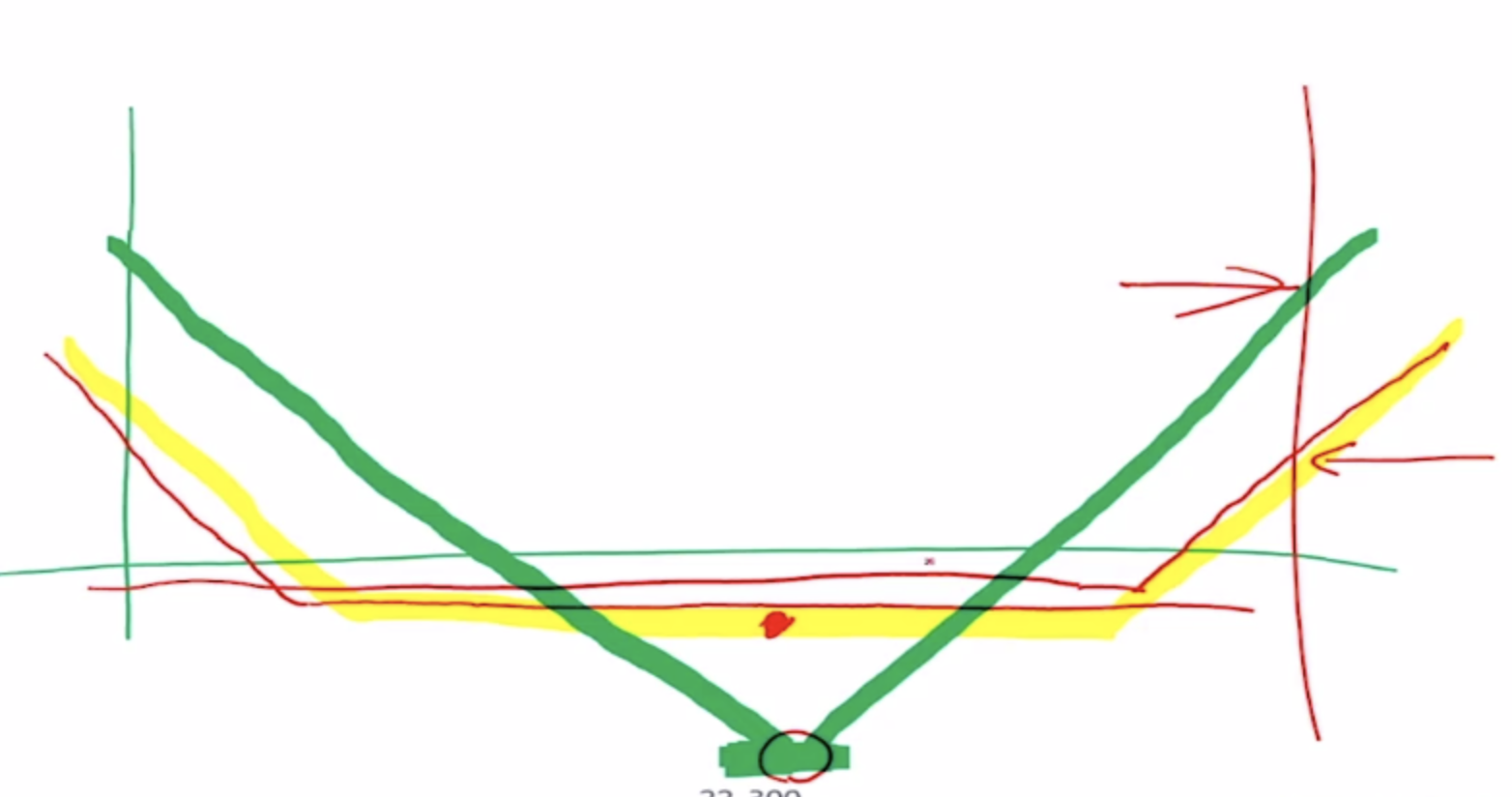
Pros: lower premium fees

Cons: lower returns

However, strangle could have a trading position that has net Vega and delta exposures (可以被做成不是围绕 current stock price 中心对称的，如向左和向右平移通过调整 call & put 的 strike price，这样可以结合 traders 对涨和跌的 expectations)

Discontinue the Carry Trade 意味着 终止 Carry Trade

Tools for Currency Management

Assume $d/f$$d/f$ direct quote, the base is foreign currency. 我们担心外币贬值，所以产生一下策略

This is a trade-off between risk-averse and hedging frequency. 一般越risk averse 越需要full hedge，但是 full hedge 成本高，所以有时 cost-effecitve way 是 dynamic hedge

Forward / Future Contracts for Hedging

Static hedge -> 由于 value of foreign asset changes -> dynamic hedge

Roll hedge 的意思是：

• 假设持有外国资产 A，在 t -1时刻 用 forward fx rate 卖出 t 时刻的外国资产 A。到 t 时点时，为卖出A的外币获得本币，fx rate 为t时刻约定的forward rate

• 在 t 时点，同时用 spot rate 花本币 买入外币，对冲掉上述交易。钆差即为 roll yield

• 在 t 时点时，外国资产的价格可能由A变为了 B。那么在t时点重复，用forward rate卖出B的外币。etc in a loop and roll over

Roll Yield / Roll Return $=\frac{F-S}{S}$$=\frac{F-S}{S}$

• Forward vs. Futures Justifications:

  1. A forward contract is less expensive.

  2. A forward contract has greater liquidity.

  • A forward contract is more suitable because in comparison to a futures contract, a forward contract is more flexible in terms of currency pair, settlement date, and transaction amount. Forward contracts are also simpler than futures contracts from an administrative standpoint owing to the absence of margin requirements, reducing portfolio management expense. Finally, forward contracts are more liquid than futures for trading in large sizes because the daily trade volume for OTC currency forward contracts dwarfs those for exchange-traded futures contracts.

Over/Under Hedged

i.g. 在未来会收到 100 US Asset，then enter a forward contract 卖100 USD 换 CNY

如果 forward contract 是 卖 120 USD 换 CNY 那么 over hedged

如果 forward contract 是 卖 80 USD 换 CNY 那么 under hedged

Options

Protective Put using OTM Options

• ATM Options are expense

• keep some downside risks as well as upside potential

Risk Reversal

Long put OTM, short call OTM ( the underlying asset is the currency )

may reduce the cost, as we short a option

Bear Put Spread

buy an OTM put and wrote a deeper OTM put with same maturity

Seagull

one type: bear put spread position with a short call position

Exotic Options

• Asian Options = $max(S_T-ave,0)$$\max(S_T - ave,0)$

• Digital Option

  

• Knock-in Options (trigger once touch a pre-specificed level)

• Knock-out Options (exit once triggered)

Hedging Multiple Currencies & Emerging Market Currency Management

Emerging mkt 特点

• return probability distributions for emerging market investments exhibit fatter tails 两边极值的概率高

• negative skew when compared with developed market (normal) distributions. 负的收益可能性多

基于上述两个原因 prob dist 不一样，导致很多ratio失效，VaR不准等 ratios are misleading

Short-term stability in emerging markets can give investors a false sense of overconfidence and thereby encourage over-positioning based on the illusion of normally distributed returns

Hedging Multiple Currencies

• Cross hedge (proxy hedge): hedge with an instrument that is not the same as the exposure 通过hedge 与目标相关的资产，如原要hedge 航空燃油，实际 hedge 原油，这样可以达成相同的效果

• Macro Hedge: focus on the entire portfolio, not individual assets or currency pair,, as assets themselves inside the portfolio might hedge themselves, so we care what left from the entire portfolio

• Minimum-variance hedge ratio: using OLS to get the cross hedging ratio ($\beta$$\beta$​, the slope in regression is the optimal hedging ratio).

  $HedgeRatio=corr(x,y)\times STD.X\times STD.Y$$Hedge Ratio = corr (x,y)\times STD. X \times STD. Y$​

  $Asset\ast HR=MinimumVarHedge$$Asset * HR = MinimumVarHedge$

Emerging Mkt Currency Management

• Might have higher trading costs

  • Larger ask bid spread

  • Crosses in currency pair (coz might not have direct pair)

• Might have Capital Control in the emerging mkt, so use non-deliverable forwards (NDFs) 不直接交还本金，cash settled rather than physically settled

NDF Characteristics:

• Counter-party risk

• Cash settlement

• the pricing of NDFs may differ from what is expected on the basis of arbitrage conditions.

Hedging to Achieve the Target

Interest Rate Swap

$D_{fixReceiver}=D_{fix}-D_{float}>0$$D_{fixReceiver} = D_{fix}- D_{float}>0$

Duration of floating-rate bond is about half of reset period

Bond Portfolio Duration Adjustment

$Bond\times MDu{r}_p+NP\times MDu{r}_s=Bond\times MDu{r}_{Target}$$Bond \times MDur_p + NP \times MDur_s = Bond \times MDur_{Target}$

$NP=\frac{MDu{r}_T-MDu{r}_p}{Mdu{r}_s}$$NP = \frac{MDur_T - MDur_p}{Mdur_s}$

$MDu{r}_s$$MDur_s$ is the modified duration of swap, $MDu{r}_p$$MDur_p$ is the current modified duration, $MDu{r}_T$$MDur_T$ is the target modified duration.

Eurodollar Futures

$BPV=NotionalValue\times 1bp\times \frac{90}{360}=25$$BPV=NotionalValue\times 1bp \times \frac{90}{360}=25$

Time Horizon is set to be 90 days

Notional Value is set to be 1 million

Fixed-Income Future

$BP{V}_p+BP{V}_f\times BPVHR=BP{T}_T$$BPV_p + BPV_f \times BPVHR = BPT_T$

$BP{V}_f\times CF=BP{V}_{CTD}$$BPV_f \times CF = BPV_{CTD}$

$BPVHR=\frac{BP{T}_T-BP{V}_P}{BP{V}_{CTD}}\times CF$$BPVHR = \frac{BPT_T - BPV_P}{BPV_{CTD}}\times CF$

Equity Future Beta

${\beta }_S\times S+N_f\times {\beta }_f={\beta }_T\times S$$\beta_S \times S + N_f \times \beta_f = \beta_T \times S$

Short Summary

If the target is $\beta =0$$\beta=0$ or $MDu{r}_t=0$$MDur_t =0$ , then just set RHS of eq to be zero.

• Long Position of T-bond Future / Stock Index Future would increase BPV Duration / Beta

• Short Position of T-bond Future / Stock Index Future would decrease BPV Duration / Beta

Variance Swap

$VarianceNotional=\frac{VegaNotional}{2\times StrikePrice}$$Variance\ Notional = \frac{Vega\ Notional}{2\times StrikePrice}$

Strike $X$$X$ is the expected future variance of the underlying, expressed as volatility (not variance)

$N_{vega}(\frac{{\sigma }^2-X^2}{2\times Strike})=N_{var}({\sigma }^2-X^2)$$N_{vega}(\frac{\sigma^2 - X^2}{2\times Strike}) = N_{var}(\sigma^2 - X^2)$

Value of the Variance Swap

站在 t 时点，variance swap的价值是多少。在 t 时点， [0,t]已经过去了，所以可以算出来 realised vol。[t,T]未发生，所以 用 implied vol or fair strike

$V_t=N_{var}\times P{V}_t\times [(\frac{t}{T}\times R{V}_{0,t}^2+\frac{T-t}{T}\times I{V}_{t,T}^2)-X^2]$$V_t = N_{var} \times PV_t \times \bigg[( \frac{t}{T}\times RV_{0,t}^2 + \frac{T-t}{T}\times IV_{t,T}^2) - X^2 \bigg]$

discount at $1+r\times \frac{T-t}{T}$$1+r\times\frac{T-t}{T}$

• N_var is variance notional

• RV is realised vol

• IV is Implied vol / fair strike

• X - original strike

• () 内相当于 换的 var的加权平均，X^2 为最开始约定的 strike variance。求PV现值，求 notional value

$VarianceNotional=\frac{VegaNotional}{2X}$$VarianceNotional = \frac{VegaNotional}{2X}$r