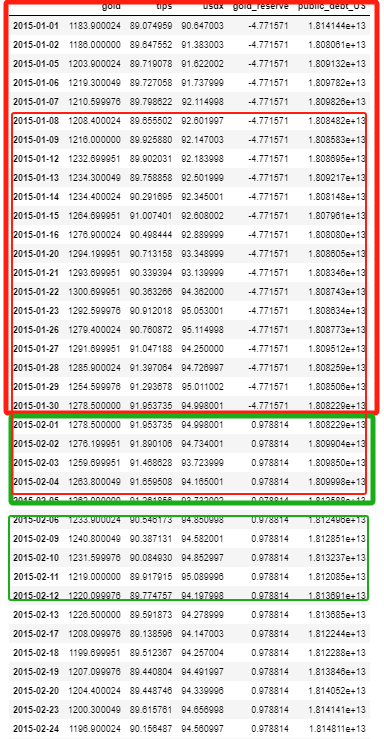
Use the panel data of the red block to predict the mean of green block. Then, roll it.
import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt
import yfinance as yf
import requests
import cufflinks as cf; cf.go_offline()
plt.style.use('fivethirtyeight')
# Define the start and end dates for the data
start_date = '2010-01-01'
# # Retrieve the data
# # Gold Price
data_gold = yf.download('GC=F', start=start_date)
# # TIPS
data_tips = yf.download('TIP', start=start_date)
# # USDollar Index
data_usdindex = yf.download('DX=F', start=start_date)
price_gold = data_gold['Adj Close'].rename('gold')
price_tips = data_tips['Adj Close'].rename('tips')
price_usdindex = data_usdindex['Adj Close'].rename('usdx')
df = pd.concat([price_gold, price_tips, price_usdindex],axis=1)
df_diff = df.diff()
df.to_csv(r'./Data/data_from_yfinance.csv')
[*********************100%%**********************] 1 of 1 completed [*********************100%%**********************] 1 of 1 completed [*********************100%%**********************] 1 of 1 completed
start_date = '2010-01-01'
df_from_yf = pd.read_csv(r'./Data/data_from_yfinance.csv', index_col='Date', parse_dates=True)
df_from_yf
| gold | tips | usdx | |
|---|---|---|---|
| Date | |||
| 2010-01-04 | 1117.699951 | 73.639183 | 77.830002 |
| 2010-01-05 | 1118.099976 | 73.879532 | 77.849998 |
| 2010-01-06 | 1135.900024 | 73.688652 | 77.654999 |
| 2010-01-07 | 1133.099976 | 73.801781 | 78.105003 |
| 2010-01-08 | 1138.199951 | 73.957268 | 77.654999 |
| ... | ... | ... | ... |
| 2024-04-16 | 2390.800049 | 105.349998 | 106.065002 |
| 2024-04-17 | 2371.699951 | 105.760002 | 105.764000 |
| 2024-04-18 | 2382.300049 | 105.620003 | 105.982002 |
| 2024-04-19 | 2398.399902 | 105.779999 | 105.984001 |
| 2024-04-22 | 2382.699951 | NaN | 105.885002 |
3600 rows × 3 columns
df_from_yf.iplot(y='gold', secondary_y = [ 'tips', 'usdx'])
df_from_yf.corr()
| gold | tips | usdx | |
|---|---|---|---|
| gold | 1.000000 | 0.734716 | 0.240488 |
| tips | 0.734716 | 1.000000 | 0.616567 |
| usdx | 0.240488 | 0.616567 | 1.000000 |
df_from_yf[df_from_yf.index>'2020'].corr()
| gold | tips | usdx | |
|---|---|---|---|
| gold | 1.000000 | 0.072961 | 0.102308 |
| tips | 0.072961 | 1.000000 | -0.609331 |
| usdx | 0.102308 | -0.609331 | 1.000000 |
df_from_yf[df_from_yf.index > '2020'].iplot(y='gold', secondary_y = [ 'tips', 'usdx'])
df_from_yf[df_from_yf.index>'2023'].corr()
| gold | tips | usdx | |
|---|---|---|---|
| gold | 1.000000 | 0.516854 | 0.000794 |
| tips | 0.516854 | 1.000000 | -0.676702 |
| usdx | 0.000794 | -0.676702 | 1.000000 |
df_from_yf[df_from_yf.index > '2023'].iplot(y='gold', secondary_y = [ 'tips', 'usdx'])
Periodically download from the website
https://www.gold.org/goldhub/data/gold-reserves-by-country
2024April: https://www.gold.org/download/file/7741/1
start_date = '2015-01-01'
df_reserve_change = pd.read_excel(r'./Data/Changes_latest_as_of_Apr2024_IFS.xlsx', sheet_name='Monthly',skiprows=7, parse_dates=True, index_col='Country')
df_reserve_change = df_reserve_change.T.iloc[2:,]
df_reserve_change.index = pd.to_datetime(df_reserve_change.index)
df_reserve_change = df_reserve_change[df_reserve_change.index >= start_date]
df_reserve_change.cumsum()[df_reserve_change.sum().sort_values()[-10:].index].iplot()
df_gold_reserve = df_reserve_change.sum(axis=1).cumsum()
df_gold_reserve.name = 'gold_reserve'
df_gold_reserve.iplot()
https://fiscaldata.treasury.gov/datasets/debt-to-the-penny/debt-to-the-penny
# Define the API endpoint URL
base_url = "https://api.fiscaldata.treasury.gov/services/api/fiscal_service/"
endpoint = "v2/accounting/od/debt_to_penny"
Num_Days = 252 * 10
parameters = f'?sort=-record_date&page[number]=1&page[size]={Num_Days}'
full_url = base_url + endpoint + parameters
# Make a GET request to the API
response = requests.get(full_url)
# Check if the request was successful (status code 200)
if response.status_code == 200:
# Parse the JSON response
data = response.json()
dict_debt = {}
# Access the data from the response
for entry in data["data"]:
# print(f"Record Date: {entry['record_date']}, Debt to Penny: {entry['tot_pub_debt_out_amt']}")
dict_debt[entry['record_date']] = entry['tot_pub_debt_out_amt']
else:
print(f"Failed to retrieve data. Status code: {response.status_code}")
df_publicDebtUS = pd.Series(dict_debt, name = 'public_debt_US')
df_publicDebtUS = df_publicDebtUS.astype('f')
df_publicDebtUS.index = pd.to_datetime(df_publicDebtUS.index)
df_publicDebtUS.sort_index().iplot()
df = pd.concat([df_from_yf, df_gold_reserve, df_publicDebtUS],axis=1)
df = df.fillna(method='ffill') # front fill all NAN with previously available figure
df = df.dropna()
# df = df[df.index > '2020']
# Save DataSet
df.to_csv(r'./Data/DataSet.csv')
def run_regression(df, robust = False, constant = True):
"""
the first column is the Y
the rest are X
"""
# Split the DataFrame into the dependent variable (Y) and independent variables (X)
Y = df.iloc[:, 0] # First column
X = df.iloc[:, 1:] # Remaining columns
# Add a constant to the independent variables (intercept)
X = sm.add_constant(X)
if not robust: # if robust is switched off
# Fit the regression model
model = sm.OLS(Y, X).fit()
else:
# fit the model with robust s.e.
model = sm.OLS(Y, X).fit(cov_type='HC3') # Use HC3 for robust standard errors
# Print the model summary
print(model.summary())
return model
model = run_regression(df)
OLS Regression Results
==============================================================================
Dep. Variable: gold R-squared: 0.932
Model: OLS Adj. R-squared: 0.932
Method: Least Squares F-statistic: 1.095e+04
Date: Mon, 22 Apr 2024 Prob (F-statistic): 0.00
Time: 13:18:56 Log-Likelihood: -13938.
No. Observations: 2393 AIC: 2.788e+04
Df Residuals: 2389 BIC: 2.791e+04
Df Model: 3
Covariance Type: nonrobust
==================================================================================
coef std err t P>|t| [0.025 0.975]
----------------------------------------------------------------------------------
const 0.0095 0.001 7.293 0.000 0.007 0.012
tips 9.4253 0.242 38.957 0.000 8.951 9.900
usdx -6.5777 0.245 -26.874 0.000 -7.058 -6.098
gold_reserve -0.0240 0.005 -4.967 0.000 -0.033 -0.014
public_debt_US 5.247e-11 1.29e-12 40.795 0.000 4.99e-11 5.5e-11
==============================================================================
Omnibus: 195.470 Durbin-Watson: 0.026
Prob(Omnibus): 0.000 Jarque-Bera (JB): 299.057
Skew: 0.629 Prob(JB): 1.15e-65
Kurtosis: 4.190 Cond. No. 1.07e+15
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 1.07e+15. This might indicate that there are
strong multicollinearity or other numerical problems.
if seperate with the train and test sets
def plot_predict_model(df_full, loc_train = 0.8, loc_test = 0.2):
# seperate the train / test set
set_train = df[:int(len(df)*loc_train)]
set_test = df[int(len(df)*(1-loc_test)):]
# train the model using the train set
temp_model = run_regression(set_train)
# predict and plot
y_predicted = set_test.iloc[:,1:].shift(1) @ temp_model.params[1:] + temp_model.params[0] # use past 1 day data to estimate the next day
y_predicted.name = 'predicted'
y_real = set_test.iloc[:,0]
results = pd.concat([y_predicted, y_real], axis=1).iplot()
return results
results = plot_predict_model(df, loc_train=1)
OLS Regression Results
==============================================================================
Dep. Variable: gold R-squared: 0.932
Model: OLS Adj. R-squared: 0.932
Method: Least Squares F-statistic: 1.095e+04
Date: Mon, 22 Apr 2024 Prob (F-statistic): 0.00
Time: 13:18:56 Log-Likelihood: -13938.
No. Observations: 2393 AIC: 2.788e+04
Df Residuals: 2389 BIC: 2.791e+04
Df Model: 3
Covariance Type: nonrobust
==================================================================================
coef std err t P>|t| [0.025 0.975]
----------------------------------------------------------------------------------
const 0.0095 0.001 7.293 0.000 0.007 0.012
tips 9.4253 0.242 38.957 0.000 8.951 9.900
usdx -6.5777 0.245 -26.874 0.000 -7.058 -6.098
gold_reserve -0.0240 0.005 -4.967 0.000 -0.033 -0.014
public_debt_US 5.247e-11 1.29e-12 40.795 0.000 4.99e-11 5.5e-11
==============================================================================
Omnibus: 195.470 Durbin-Watson: 0.026
Prob(Omnibus): 0.000 Jarque-Bera (JB): 299.057
Skew: 0.629 Prob(JB): 1.15e-65
Kurtosis: 4.190 Cond. No. 1.07e+15
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 1.07e+15. This might indicate that there are
strong multicollinearity or other numerical problems.
VIX also shows statistically significant
# # USDollar Index
data_vix = yf.download('^VIX', start=start_date)
price_vix = data_vix['Adj Close'].rename('vix')
df_temp = pd.concat([df, price_vix], axis =1).dropna()
[*********************100%%**********************] 1 of 1 completed
model_temp = run_regression(df_temp)
OLS Regression Results
==============================================================================
Dep. Variable: gold R-squared: 0.934
Model: OLS Adj. R-squared: 0.934
Method: Least Squares F-statistic: 8328.
Date: Mon, 22 Apr 2024 Prob (F-statistic): 0.00
Time: 13:18:57 Log-Likelihood: -13585.
No. Observations: 2340 AIC: 2.718e+04
Df Residuals: 2335 BIC: 2.721e+04
Df Model: 4
Covariance Type: nonrobust
==================================================================================
coef std err t P>|t| [0.025 0.975]
----------------------------------------------------------------------------------
const 0.0057 0.001 3.896 0.000 0.003 0.009
tips 8.9515 0.248 36.114 0.000 8.465 9.438
usdx -6.7403 0.244 -27.629 0.000 -7.219 -6.262
gold_reserve -0.0326 0.005 -6.622 0.000 -0.042 -0.023
public_debt_US 5.437e-11 1.31e-12 41.611 0.000 5.18e-11 5.69e-11
vix 1.9966 0.244 8.193 0.000 1.519 2.475
==============================================================================
Omnibus: 160.805 Durbin-Watson: 0.029
Prob(Omnibus): 0.000 Jarque-Bera (JB): 251.765
Skew: 0.543 Prob(JB): 2.14e-55
Kurtosis: 4.185 Cond. No. 1.10e+15
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 1.1e+15. This might indicate that there are
strong multicollinearity or other numerical problems.
results = plot_predict_model(df_temp, loc_train = 1)
OLS Regression Results
==============================================================================
Dep. Variable: gold R-squared: 0.932
Model: OLS Adj. R-squared: 0.932
Method: Least Squares F-statistic: 1.095e+04
Date: Mon, 22 Apr 2024 Prob (F-statistic): 0.00
Time: 13:18:57 Log-Likelihood: -13938.
No. Observations: 2393 AIC: 2.788e+04
Df Residuals: 2389 BIC: 2.791e+04
Df Model: 3
Covariance Type: nonrobust
==================================================================================
coef std err t P>|t| [0.025 0.975]
----------------------------------------------------------------------------------
const 0.0095 0.001 7.293 0.000 0.007 0.012
tips 9.4253 0.242 38.957 0.000 8.951 9.900
usdx -6.5777 0.245 -26.874 0.000 -7.058 -6.098
gold_reserve -0.0240 0.005 -4.967 0.000 -0.033 -0.014
public_debt_US 5.247e-11 1.29e-12 40.795 0.000 4.99e-11 5.5e-11
==============================================================================
Omnibus: 195.470 Durbin-Watson: 0.026
Prob(Omnibus): 0.000 Jarque-Bera (JB): 299.057
Skew: 0.629 Prob(JB): 1.15e-65
Kurtosis: 4.190 Cond. No. 1.07e+15
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 1.07e+15. This might indicate that there are
strong multicollinearity or other numerical problems.
That Preidiction is counter intuitive, as the simply model might hardly perform better than Deep Learning model in prediction.
Let's see how a LSTM works then.
SPLIT_RATE = 0.80
SPLIT = int(len(df) * SPLIT_RATE)
df_train = df.iloc[:SPLIT,]
df_test = df.iloc[SPLIT:,]
df_train_X = df_train.copy()
df_train_y = df_train.iloc[:,0]
df_train_X
| gold | tips | usdx | gold_reserve | public_debt_US | |
|---|---|---|---|---|---|
| 2015-01-01 | 1183.900024 | 89.074951 | 90.647003 | -4.771571 | 1.814144e+13 |
| 2015-01-02 | 1186.000000 | 89.647568 | 91.383003 | -4.771571 | 1.808061e+13 |
| 2015-01-05 | 1203.900024 | 89.719139 | 91.622002 | -4.771571 | 1.809132e+13 |
| 2015-01-06 | 1219.300049 | 89.727066 | 91.737999 | -4.771571 | 1.809782e+13 |
| 2015-01-07 | 1210.599976 | 89.798637 | 92.114998 | -4.771571 | 1.809826e+13 |
| ... | ... | ... | ... | ... | ... |
| 2022-06-01 | 1843.300049 | 110.265816 | 102.528999 | 3578.961501 | 3.044098e+13 |
| 2022-06-02 | 1866.500000 | 110.774353 | 101.832001 | 3578.961501 | 3.042566e+13 |
| 2022-06-03 | 1845.400024 | 111.414734 | 102.160004 | 3578.961501 | 3.041255e+13 |
| 2022-06-06 | 1839.199951 | 110.689590 | 102.446999 | 3578.961501 | 3.042089e+13 |
| 2022-06-07 | 1847.500000 | 110.953270 | 102.324997 | 3578.961501 | 3.041759e+13 |
1914 rows × 5 columns
from sklearn.preprocessing import StandardScaler
standerdiser_X = StandardScaler()
standerdiser_y = StandardScaler()
df_train_scaled_X = standerdiser_X.fit_transform(df_train_X)
df_train_scaled_y = standerdiser_y.fit_transform(df_train_y.to_numpy().reshape(-1,1))
Use the panel data of the red block to predict the mean of green block. Then, roll it.

duration = 21 # 21 workings days means 1 month
num_records = len(df_train)
window = 5
X_train = []
y_train = []
for i in range(duration, num_records, window):
X_train.append(df_train_scaled_X[i - duration:i]) # use past 21-day data, rolling-(ly)
y_train.append(df_train_scaled_y[i:i + window].mean()) # to estimate the future 5-day means
X_train, y_train = np.array(X_train), np.array(y_train)
from keras.models import Sequential
from keras.layers import Dense, LSTM, Dropout
model = Sequential()
model.add(LSTM(units = 50, return_sequences=True))
model.add(Dropout(0.2))
model.add(LSTM(units=50))
model.add(Dropout(0.1))
model.add(Dense(1))
model.compile(optimizer='adam', loss = 'mean_squared_error')
model.fit(X_train, y_train, epochs = 100, batch_size = 64, verbose=2)
Epoch 1/100 6/6 - 3s - 559ms/step - loss: 0.3978 Epoch 2/100 6/6 - 0s - 18ms/step - loss: 0.1049 Epoch 3/100 6/6 - 0s - 16ms/step - loss: 0.0653 Epoch 4/100 6/6 - 0s - 17ms/step - loss: 0.0574 Epoch 5/100 6/6 - 0s - 17ms/step - loss: 0.0495 Epoch 6/100 6/6 - 0s - 17ms/step - loss: 0.0407 Epoch 7/100 6/6 - 0s - 14ms/step - loss: 0.0340 Epoch 8/100 6/6 - 0s - 17ms/step - loss: 0.0337 Epoch 9/100 6/6 - 0s - 17ms/step - loss: 0.0284 Epoch 10/100 6/6 - 0s - 19ms/step - loss: 0.0293 Epoch 11/100 6/6 - 0s - 17ms/step - loss: 0.0254 Epoch 12/100 6/6 - 0s - 16ms/step - loss: 0.0269 Epoch 13/100 6/6 - 0s - 19ms/step - loss: 0.0223 Epoch 14/100 6/6 - 0s - 17ms/step - loss: 0.0256 Epoch 15/100 6/6 - 0s - 17ms/step - loss: 0.0208 Epoch 16/100 6/6 - 0s - 19ms/step - loss: 0.0215 Epoch 17/100 6/6 - 0s - 17ms/step - loss: 0.0214 Epoch 18/100 6/6 - 0s - 20ms/step - loss: 0.0203 Epoch 19/100 6/6 - 0s - 16ms/step - loss: 0.0193 Epoch 20/100 6/6 - 0s - 17ms/step - loss: 0.0191 Epoch 21/100 6/6 - 0s - 17ms/step - loss: 0.0189 Epoch 22/100 6/6 - 0s - 16ms/step - loss: 0.0216 Epoch 23/100 6/6 - 0s - 17ms/step - loss: 0.0200 Epoch 24/100 6/6 - 0s - 17ms/step - loss: 0.0208 Epoch 25/100 6/6 - 0s - 17ms/step - loss: 0.0191 Epoch 26/100 6/6 - 0s - 17ms/step - loss: 0.0192 Epoch 27/100 6/6 - 0s - 17ms/step - loss: 0.0173 Epoch 28/100 6/6 - 0s - 17ms/step - loss: 0.0184 Epoch 29/100 6/6 - 0s - 15ms/step - loss: 0.0214 Epoch 30/100 6/6 - 0s - 17ms/step - loss: 0.0181 Epoch 31/100 6/6 - 0s - 16ms/step - loss: 0.0174 Epoch 32/100 6/6 - 0s - 17ms/step - loss: 0.0187 Epoch 33/100 6/6 - 0s - 20ms/step - loss: 0.0197 Epoch 34/100 6/6 - 0s - 16ms/step - loss: 0.0186 Epoch 35/100 6/6 - 0s - 16ms/step - loss: 0.0175 Epoch 36/100 6/6 - 0s - 16ms/step - loss: 0.0176 Epoch 37/100 6/6 - 0s - 19ms/step - loss: 0.0183 Epoch 38/100 6/6 - 0s - 17ms/step - loss: 0.0189 Epoch 39/100 6/6 - 0s - 19ms/step - loss: 0.0168 Epoch 40/100 6/6 - 0s - 16ms/step - loss: 0.0190 Epoch 41/100 6/6 - 0s - 19ms/step - loss: 0.0171 Epoch 42/100 6/6 - 0s - 17ms/step - loss: 0.0166 Epoch 43/100 6/6 - 0s - 17ms/step - loss: 0.0164 Epoch 44/100 6/6 - 0s - 16ms/step - loss: 0.0150 Epoch 45/100 6/6 - 0s - 18ms/step - loss: 0.0160 Epoch 46/100 6/6 - 0s - 16ms/step - loss: 0.0150 Epoch 47/100 6/6 - 0s - 15ms/step - loss: 0.0163 Epoch 48/100 6/6 - 0s - 17ms/step - loss: 0.0194 Epoch 49/100 6/6 - 0s - 17ms/step - loss: 0.0178 Epoch 50/100 6/6 - 0s - 17ms/step - loss: 0.0161 Epoch 51/100 6/6 - 0s - 16ms/step - loss: 0.0155 Epoch 52/100 6/6 - 0s - 19ms/step - loss: 0.0158 Epoch 53/100 6/6 - 0s - 17ms/step - loss: 0.0161 Epoch 54/100 6/6 - 0s - 17ms/step - loss: 0.0170 Epoch 55/100 6/6 - 0s - 17ms/step - loss: 0.0155 Epoch 56/100 6/6 - 0s - 16ms/step - loss: 0.0135 Epoch 57/100 6/6 - 0s - 17ms/step - loss: 0.0142 Epoch 58/100 6/6 - 0s - 17ms/step - loss: 0.0156 Epoch 59/100 6/6 - 0s - 18ms/step - loss: 0.0151 Epoch 60/100 6/6 - 0s - 18ms/step - loss: 0.0158 Epoch 61/100 6/6 - 0s - 14ms/step - loss: 0.0154 Epoch 62/100 6/6 - 0s - 14ms/step - loss: 0.0143 Epoch 63/100 6/6 - 0s - 18ms/step - loss: 0.0154 Epoch 64/100 6/6 - 0s - 18ms/step - loss: 0.0172 Epoch 65/100 6/6 - 0s - 18ms/step - loss: 0.0143 Epoch 66/100 6/6 - 0s - 16ms/step - loss: 0.0166 Epoch 67/100 6/6 - 0s - 16ms/step - loss: 0.0174 Epoch 68/100 6/6 - 0s - 16ms/step - loss: 0.0142 Epoch 69/100 6/6 - 0s - 17ms/step - loss: 0.0157 Epoch 70/100 6/6 - 0s - 17ms/step - loss: 0.0145 Epoch 71/100 6/6 - 0s - 17ms/step - loss: 0.0144 Epoch 72/100 6/6 - 0s - 19ms/step - loss: 0.0142 Epoch 73/100 6/6 - 0s - 20ms/step - loss: 0.0144 Epoch 74/100 6/6 - 0s - 16ms/step - loss: 0.0143 Epoch 75/100 6/6 - 0s - 17ms/step - loss: 0.0139 Epoch 76/100 6/6 - 0s - 17ms/step - loss: 0.0141 Epoch 77/100 6/6 - 0s - 17ms/step - loss: 0.0142 Epoch 78/100 6/6 - 0s - 19ms/step - loss: 0.0144 Epoch 79/100 6/6 - 0s - 17ms/step - loss: 0.0128 Epoch 80/100 6/6 - 0s - 17ms/step - loss: 0.0143 Epoch 81/100 6/6 - 0s - 17ms/step - loss: 0.0132 Epoch 82/100 6/6 - 0s - 19ms/step - loss: 0.0140 Epoch 83/100 6/6 - 0s - 17ms/step - loss: 0.0137 Epoch 84/100 6/6 - 0s - 17ms/step - loss: 0.0125 Epoch 85/100 6/6 - 0s - 18ms/step - loss: 0.0147 Epoch 86/100 6/6 - 0s - 17ms/step - loss: 0.0139 Epoch 87/100 6/6 - 0s - 17ms/step - loss: 0.0144 Epoch 88/100 6/6 - 0s - 20ms/step - loss: 0.0130 Epoch 89/100 6/6 - 0s - 16ms/step - loss: 0.0151 Epoch 90/100 6/6 - 0s - 17ms/step - loss: 0.0140 Epoch 91/100 6/6 - 0s - 17ms/step - loss: 0.0157 Epoch 92/100 6/6 - 0s - 17ms/step - loss: 0.0168 Epoch 93/100 6/6 - 0s - 17ms/step - loss: 0.0153 Epoch 94/100 6/6 - 0s - 17ms/step - loss: 0.0137 Epoch 95/100 6/6 - 0s - 17ms/step - loss: 0.0147 Epoch 96/100 6/6 - 0s - 17ms/step - loss: 0.0139 Epoch 97/100 6/6 - 0s - 16ms/step - loss: 0.0133 Epoch 98/100 6/6 - 0s - 17ms/step - loss: 0.0131 Epoch 99/100 6/6 - 0s - 17ms/step - loss: 0.0118 Epoch 100/100 6/6 - 0s - 18ms/step - loss: 0.0130
<keras.src.callbacks.history.History at 0x1deb8a48990>
df_test_standardised = standerdiser_X.transform(df_test)
df_test_standardised.shape
(479, 5)
duration = 21
num_records_test = len(df_test_standardised)
window = 5
df_test_predict = []
y_true = []
list_index = []
for i in range(duration, num_records_test, window):
df_test_predict.append(df_test_standardised[i-duration:i])
y_true.append(df_test[i : i + window]['gold'].mean())
list_index.append(df_test.index[i])
df_test_predict, y_true = np.array(df_test_predict), np.array(y_true)
print(df_test_predict.shape)
print(y_true.shape)
(92, 21, 5) (92,)
y_predicted = model.predict(df_test_predict)
3/3 ━━━━━━━━━━━━━━━━━━━━ 1s 184ms/step
y_predicted_result = standerdiser_y.inverse_transform(y_predicted)
y_predicted_result.shape
(92, 1)
table_result = pd.DataFrame([y_true, y_predicted_result.reshape(1,-1)[0]], columns=list_index).T
table_result = table_result.rename(columns={0:'TrueValue',1:'Predicted'})
table_result.iplot()