- In the monetarist view, the price level is determined by the amount of money in the economy.
- Inflation is everywhere a monetary phenomenon.
- Inflation is too much money chasing too few goods
Assume a model that, instead of using the money for transactions, agents just get happy holding some money in their pockets.
The optimisation problem becomes to be,
$$ \max_{c_t, b_{t+1},M_t} \sum_{t=0}^{\infty} \beta^t [u(c_t)+v(\frac{M_t}{p_t})] $$
$$s.t. \quad p_t c_t +\frac{b_{t+1}}{1+i_{t+1}}+M_t=b_t+\underbrace{p_t y}_{current\ sales\ withou\ lages}+M_{t-1}$$
F.O.C.
$$ u'(c_t)=\beta (1+i_{t+1})\frac{p_t}{p_{t+1}}u'(c_{t+1}) $$
$$ u'(c_t)-v'(\frac{M_t}{p_t})=\beta \frac{p_t}{p_{t+1}}u'(c_{t+1}) $$
Now assume that money supply follows \(M_{t+1}=(1+\mu)M_t\). Also assume government spending is zero, so all seignorage is redistributed as a (negative) lum-sum tax. ENdowments are constant and given by \(y\).
Then the constraint,
$$ u'(c_t)-v'(\frac{M_t}{p_t})=\beta \frac{p_t}{p_{t+1}}u'(c_{t+1}) $$
can be written as,
$$u'(y)-v'(m_t)=\beta \frac{1}{1+\pi_t}u'(y)$$
, where I impose that \(y=c+g\), with \(g=0\), \(m_t=\frac{M_t}{p_t}\), and define \(1+\pi_t=\frac{p_{t+1}}{p_t}\).
Notice that,
$$ \underbrace{\frac{m_{t+1}}{m_t}}_{ratio\ of\ real\ money\ balance}=\frac{ \frac{M_{t+1}}{p_{t+1}} }{ \frac{M_t}{p_t} }=\frac{M_{t+1}}{M_t}\times \frac{P_t}{P_{t+1}}=\frac{1+\mu}{1+\pi_t} $$
so the Euler equation
$$ u'(y)-v'(m_t)=\beta \frac{1}{1+\pi_t}u'(y) $$
becomes (by replacing \(\frac{1}{1+\pi}=\frac{m_{t+1}}{m_t}\frac{1}{1+\mu}\)),
$$ m_{t+1}=\frac{1+\mu}{\beta}\frac{u'(y)-v'(m_t)}{u'(y)}m_t $$
Showing the relationship between real money supply over periods.
Find Solutions of The Euler Equation
- At the Steady State
Assume\(m\neq0\). Let \(m_t=m_{t+1}=…=m^*\) and \(m^*>0\) at the steady state,
$$ 1=\frac{1+\mu}{\beta}\frac{u'(y)-v'(m^*)}{u'(y)} $$
Clearly, there is a \(m^*>0\) satisfy the equation.
- \(m\rightarrow 0\)
$$ m_{t+1}=\frac{1+\mu}{\beta}\frac{u'(y)-v'(m_t)}{u'(y)}m_t $$
If \( \lim_{m\rightarrow 0}v'(m)m=0\), then \(m^*=0\) is also a steady state equilibrium.
- P.S. \(u'(y)=v'(m”)\)
In addition, there exists an \(m”>0\) such that
$$ u'(y)=v'(m”) $$
which implies that \(m_{t+1}\leq0\) for \(m_t\leq m”\).
The relationship could be expressed by the figure below.
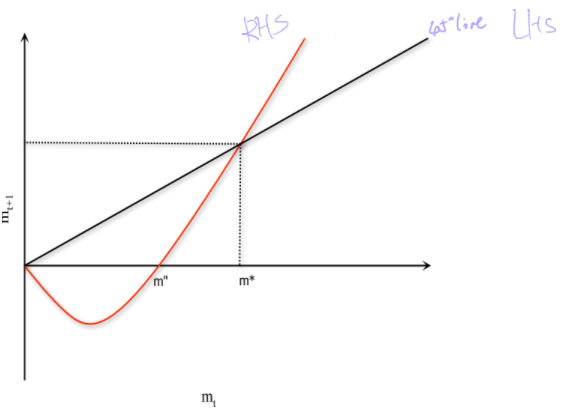
If the initial condition of \(m_t\) is at the right of \(m^*\), then RHS is always greater than the LHS and would result in \(\lim_{t \rightarrow \infty} m_t \rightarrow \infty\). No steady state and violate the transversality condition. Thus, \(m_0\) cannot be at the right of \(m^*\).
If the \(m_0\) at the left of \(m^*\), then \(m_t\) would converge to 0 (as the similar logic above). Therefore, as \(m_t \rightarrow 0\), \(p_t\ rightarrow \infty\) even if \(M_t\) keeps constant. That would lead to hyperinflation.
In that scenario, the unique equilibrium is \(m_t=m^*>0\), the price level is determined. Prices, in this case, must be growing at precisely the same rates as money, which adhere to the monetarist doctrine. However, the economy can also display speculative hyperinflation in which inflation far outpace money growth.
In addition, different forms of the RHS might lead to different results.
E.G. the concavity of RHS, the interaction point at zero, etc would all affect the equilibrium condition.
- No interaction at 0.
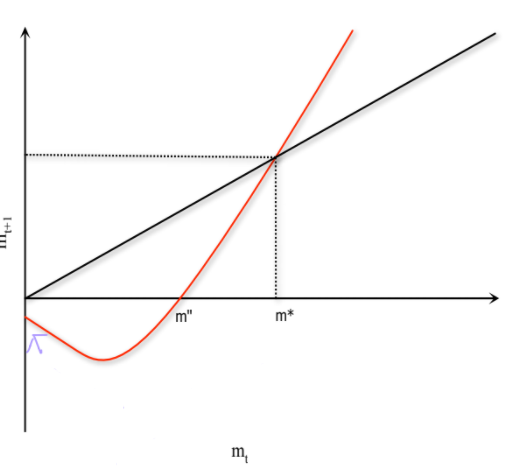
- No \(m”\)

