Based on many years of study of the Solow model, I learned different versions of it. Although all of them are talking about the same theory, there are some differences in the learning structure and functional forms of the model. Now, I revisit the Solow model mainly based on the original paper (Solow, 1956). Here is a summary of the Solow model.
Robert Solow was awarded the Nobel Prize in 1987 for his contributions to the theory of Economic Growth.
Start
All theory depends on assumptions which are not quite true. That is what makes it theory. The art of successful theorizing is to make the inevitable simplifying assumptions in such a way that the final results are not very sensitive. 1 A “crucial” assumption is one on which the conclusions do depend sensitively, and it is important that crucial assumptions be reasonably realistic. When the results of a theory seem to flow specifically from a special crucial assumption, then if the assumption is dubious, the results are suspect.
The above paragraph is the beginning of his paper. That is the first time I read this paper. It really shocks me and brings me a different understanding about economic theory.
Assumption
- Only one commodity, output as a whole. \(Y(t)\), by which output equals income.
- For each agent, \(Y(t)=consumption+saving/investing\). That is equivalent to assuming no government and net export, \(Y=C+I+G+NX\).
- Net investment equals saving. (1) \(\frac{\partial K}{\partial t}=\dot{K}=s\cdot Y(t)\).
- Output is produced by two factors, labour and capital. (2) \(Y=F(K,L)\). Also, the production function is homogenous of degree one and CRTS.
Solve
Insert (1) into (2), we would get
(3)\(\quad \dot{K}=sF(K,L) \)
As \(s\) is exogenous, thus (3) has two unknowns, so it is unable to be solved. To solve (3), we need to know something about labour.
There are mainly two ways of finding labour. Way 1: \(MPL=\frac{W}{P}\), which is the marginal productivity of labour equals real wage rate. Then, we can solve the labour supply. Way 2: take a general form. Making labour supply \(=f(W/P\). In any case, there are three unknowns, \(W,P,\) and \(L\).
However, we here assume an exogenous population growth rate \(n\). Thus,
(4) \(\quad L(t)=L_0\cdot e^{nt} \)
(easy to show \(ln(\frac{L_t}{L_{t-1}})=n\) and \(\frac{\dot{L_t}}{L_t}=n\).)
This term can be considered as the labour supply. It says that an exponentially growing labour force is offered. Employment is completely inelastic.
Put (4) into (3), we would get,
(5) \(\dot{K}=sF(K,L_0e^{nt})\).
, which is the time-path of capital accumulation under full employment.
(5) is a differential equation, and \(K(t)\) is the only variable. The solution could tell us, (all the followings are under full employment)
- the time path of capital.
- \(MPL=w\), and \(MPK=r\). The time-path of real wage rate and capital rent rate.
- By given saving rate, we would also know saving and consumptions.
We introduce a new variable\(k=\frac{K}{L}\), which is capital per capita.
Thus, \(K=kL=kL_0e^{nt}\). The, differentiate w.r.t. \(t\), we get,
$$\dot{K}=\dot{k}L+K\dot{L}=\dot{k}L_0e^{nt}+nkL_0e^{nt}$$
Combining with (5),
$$ \dot{k}L_0e^{nt}+nkL_0e^{nt}=sF(K,L_0e^{nt}) $$
$$ \dot{k}=sF(k,1)-nk $$
Graphically, (r is k in my definition).
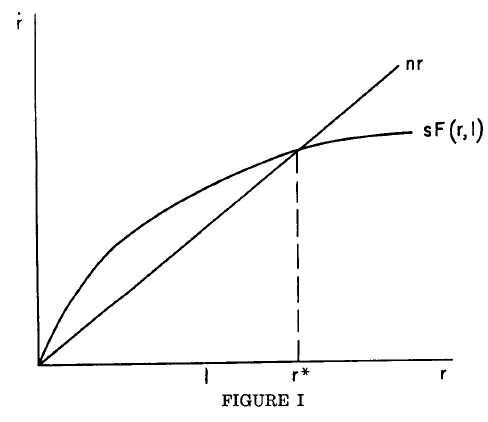
Easy to see that if the production function is increasing and diminishing and shaped as the figure above, then the interaction \(k^*\) would be a stable value (easy to show by discussing before \(k^*\) and after. e.g. if before k* then \(\dot{k}>0\), there is the accumulation of capital per capita).
Some simple math,
$$k=\frac{K}{L}$$
$$ ln(k)=ln(K)-ln(L) $$
Differentiate w.r.t. \(t\),
$$ \frac{\dot{k}}{k}= \frac{\dot{K}}{K}- \underbrace{\frac{\dot{L}}{L}}_{n} $$
When\( \frac{\dot{k}}{k} =0\), then \( \frac{\dot{K}}{K} = \frac{\dot{L}}{L}=n\). The implication is that at \(k^*\) (two lines interact, and make \( \frac{\dot{k}}{k} =0\) ) the time-path of labour equal that of capital.
In addition, for Y and y,
$$ln(Y)=ln(F(K,L))$$
Differentiate w.r.t. \(t\),
$$ \frac{\dot{Y}}{Y}=\frac{ \dot{K}F_1’+\dot{L}F_2′ }{F(K,L)} $$
By Euler’s Theorem (see math tools),
$$ \frac{\dot{Y}}{Y}=\frac{ \dot{K}F_1’+\dot{L}F_2′ }{KF’_1+LF’_2}=\frac{ \frac{\dot{K}}{KL}F’_1 +\frac{\dot{L}}{KL}F’_2}{\frac{F’_1}{L}+\frac{F’_2}{K}} $$
\frac{\dot{Y}}{Y}=\frac{ \dot{K}F_1’+\dot{L}F_2′ }{KF’_1+LF’_2}=\frac{ \frac{\dot{K}}{KL}F’_1 +\frac{\dot{L}}{KL}F’_2}{\frac{F’_1}{L}+\frac{F’_2}{K}}
\frac{\dot{Y}}{Y}= \frac{ \frac{\dot{K}}{K}\frac{F’_1}{L} +\frac{\dot{L}}{L}\frac{F’_2}{K}}{\frac{F’_1}{L}+\frac{F’_2}{K}}= \frac{n\times ( \frac{F’_1}{L}+\frac{F’_2}{K} )}{ \frac{F’_1}{L}+\frac{F’_2}{K} }
$$ \frac{\dot{Y}}{Y}=n $$
$$ y=\frac{Y}{L} $$
$$ ln(y)=ln(Y)-ln(L) $$
$$ \frac{\dot{y}}{y}= \frac{\dot{Y}}{Y}- \frac{\dot{L}}{L}=n-n=0 $$
The introduction of Solow (1956) ends there (there are analysis of applying different functional forms of production in his paper, but I would not discuss here), the following are a summary of my previous learning.
P.S. there is no depreciation in the original Solow model.
In summary, the key assumptions are: 1, the law of motion of capital accumulation \(\dot{K}=I\); 2, the shape of the production function.
Solow followed this paper with another pioneering artical, “Technical Change and the Aggregate Production Function.” Before it was published, economists had believed that capital and labour were the main causes of economic growth. But Solow showed that half of economic growth cannot be accounted for by increases in capital and labour.This unaccounted-for portion of economic growth—now called the “Solow residual”—he attributed to technological innovation.
Reference
Solow, 1956