M&M theorem (Modigliani and Miller, 1958) is used to value a firm. It states that a firm’s value is based on its ability to earn revenue plus its risk of underlying assets. The way a firm finances its operations should not affect its value.
At its most basic level, the theorem argues that, with certain assumptions in place, it is irrelevant whether a company finances its growth by borrowing, by issuing stock shares, or by reinvesting its profits.
Assumptions are 1. the markets are completely efficient; 2. there are no costs of bankruptcy or agency dynamics and no taxes.
However, there are of course taxes and costs in the reality, and the assumptions do not hold. Therefore, the M&M theorem implies that firms are more valuable if financed by debts than financed by equities. The reason is the tax shield effects of debts.
Mathematic Example
Consider two companies, same risks, same expected cash flow before interest, \( Y\).
- Co1, has debt with market value of \(D_1\). Total market value \(V_1=E_1+D_1\).
- Co2, has no debt. \(V_2=E_2\), market value of equity.
We can invest,
- Investment A: We own a fraction \(a\) (e.g. 6%) of shares in Co1z. They worth \(aE_1\) (e.g. $6,000). Expected cash flow from investment A, \(y_A\), is:
$$(y_A=\underbrace{a}_{SharesOwned} \times \underbrace{(Y-R_D D_1)}_{Co1’s EarningAfterInterest}$$
Co1 needs to pay an interest rate of its debt, \(R_D D_1\). Purchasing Co1 means only purchasing the equity of Co1, which is EV-Debts.
- Investment B: We sell the shares of Co1. We receive amount \(aE_1\) ($6,000). Then, we use this to buy shares in Co2, which is ungeared.
To Produce the same gearing and risk as investment A, we borrow a further amount worth \(aD_1\) (‘home-made gearing’ or ‘artificially gearing’), at interest rate \(R_D\), and buy more shares in Co2.
E.G. if gearing of Co1 is \( \frac{D_1}{D_1+E_1}=0.25\), then to get same gear for our investment B, we borrow \(6,000\times \frac{0.25}{0.75}=2,000\).
Expected cash flow from investment B, \( y_B\), is:
$$ y_B=\frac{aE_1+aD_1}{E_2}Y-R_D\times aD_1 = a\frac{V_1}{V_2}Y-R_D\times aD_1$$
In equilibrium, \( y_A=y_B\). Otherwise, arbitrage opportunity emerges. Therefore, we get \(V_1=V_2\).
In conclusion, gearing does not affect value (Equity plus Debt).
Implication
Since expected net cash flow (\(Y\)) and company value are the same for each company, the cost of equity for ungeared Co2 and WACC for geared Co1 must be equal. So WACC must be constant with respect to gearing.
Let the cost of equity for a company with no debt be \(R_{ungeared}\).
$$ R_{ungeared}=R_D\frac{D}{V}+R_E\frac{E}{V}=WACC$$
$$ R_{ungeared}=R_D\frac{D}{D+E}+R_E\frac{E}{D+E}=WACC$$
WACC is constant w.r.t. \(\frac{D}{V}\).
$$ R_{ungeared}(D+E)=R_DD+R_EE$$
$$ R_EE=R_{ungeared}(D+E)-R_DD $$
$$ R_E=R_{ungeared}+(R_{ungeared}-R_D)\frac{D}{E} $$
So we get a linear relation between cost of equity and D/E, assuming a constant cost of debt, assuming a constant cost of debt (and assuming \(R_{ungeared}>R_D\)). Implicly, changes in gearing structure (or how to finance the business) do not affect the WACC for a company.
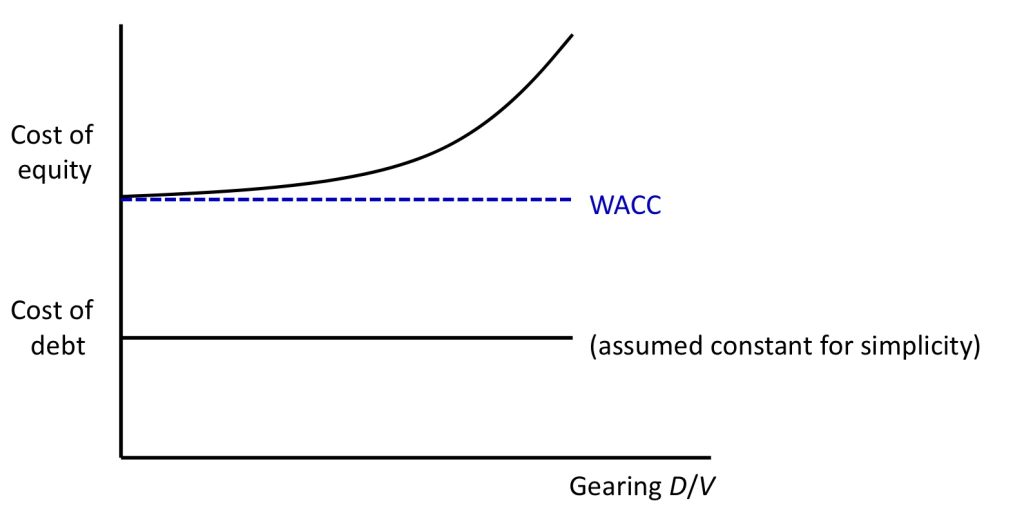
Violation of the constant debt assumption of course would make WACC unconstant.
MM Theory & Beta
In the CAPM, expected returns on assets differ because their betas differ.
So we can write,
$$ \beta_{ungeared}=\beta_{debt}\frac{D}{D+E}+\beta_{geared}\frac{E}{D+E} $$
$$\beta_{geared}=\beta_{ungeared}+(\beta_{ungeared}-\beta_{debt})\frac{D}{E}$$
, where \(\beta_{ungeared}\) denotes asset beta, and \( \beta_{geared}\) denotes actual beta of shares of a geared company (estimated from the market data).
Calculations are similar to those as above.
If assume \(\beta_{debt}=0\), then
$$ \beta_{ungeared}=\beta_{geared} \frac{E}{V}$$
$$ \beta_{geared}=\beta_{ungeared}(1+\frac{D}{E}) $$
A Modigliani-Miller Theorem for Open-Market Operations
Monetary policy determines the composition of the government’s portfolio. Fiscal policy (the size of the deficit on the current account) determines the path of net government indebtedness. Wallace showed that alternative paths of the government’s portfolio consistent with a single path of fiscal policy can be irrelevant. The irrelevance means that both the equilibrium consumption allocation and the path of the price level are independent of the path of the government’s portfolio.
Typos are there. See the original paper issued by Fed in 1979.
Reference
Modigliani, F. and Miller, M.H., 1958. The cost of capital, corporation finance and the theory of investment. The American economic review, 48(3), pp.261-297.
Wallace, N., 1981. A Modigliani-Miller theorem for open-market operations. The American Economic Review, 71(3), pp.267-274.