Derivations
We here derive why \(MRS_{x,y}=\frac{MU_x}{MU_y}\).
Let \(U(x,y)=f(x,y)\), and we know, by definition, MRS measures how many units of x is needed to trade y holding utility constant. Thus, we keep the utility function unchanged, \(U(x,y)=C\), and take differentiation and find \(-dy/dx\).
$$f(x,y) dx=C dx$$
$$ \frac{\partial f(x,y)}{x}+\frac{\partial f(x,y)}{\partial y}\frac{\partial y}{\partial x}=0 $$
$$\frac{\partial y}{\partial x}=-\frac{\frac{\partial f(x,y)}{\partial x}}{\frac{\partial f(x,y)}{\partial y}}=\frac{MU_x}{MU_y}$$
Therefore,
MRS_{x,y}=-\frac{dy}{dx}=\frac{MU_x}{MU_y}
$$|MRS_{x,y}|=-\frac{dy}{dx}=\frac{MU_x}{MU_y} $$
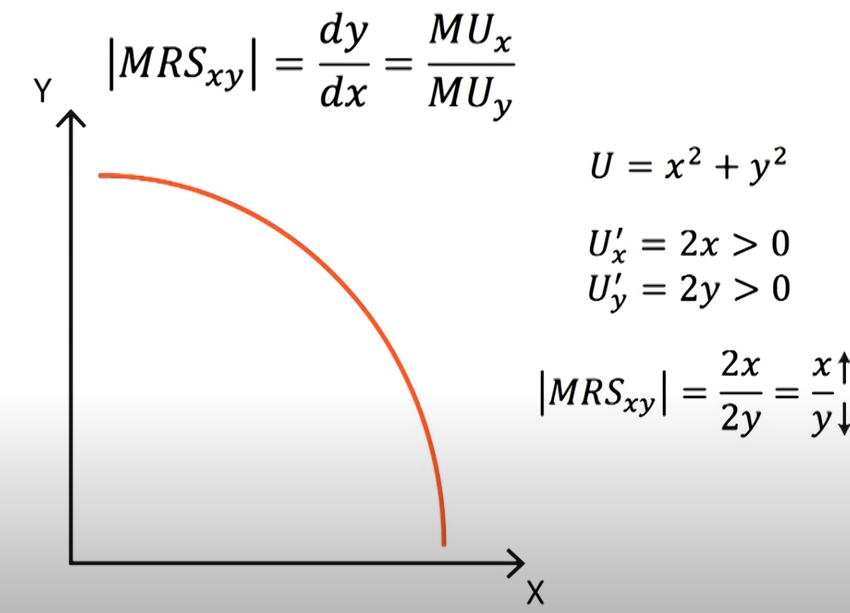
Example 1
$$U=x^2+y^2$$
$$MRS_{x,y}=\frac{MU_x}{MU_y} =\frac{x}{y}$$
Example 2
$$U=x\cdot y$$
, which is similar as the Cobb-Douglas form but has exponenets zero.
$$MRS_{x,y}=\frac{MU_x}{MU_y} =\frac{y}{x}$$

Example 3

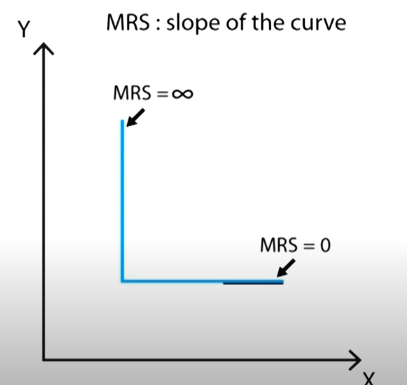
MRTS
Marginal Rate of Technical Substitution (MRTS) measures the amount of cost which a specific input can be replaced for another resource of production while maintaining a constant output.
$$MRTS_{K,L}=-\frac{\Delta K}{\Delta L}=-\frac{d K}{d L}=\frac{MP_L}{MP_K}$$
How to derive that?
Recall the Isoquant that is equivalent to the contour line of the output function. MRTS is like the slope of the isoquant line. We let,
$$Q=L^a K^b$$
Then,
$$MP_K=\frac{\partial Q}{\partial K}=b L^A K^{b-1}$$
$$MP_L=\frac{\partial Q}{\partial L}=a L^{a-1}K^b$$
$$MRTS=\frac{ b L^A K^{b-1} }{ a L^{a-1}K^b }=\frac{aK}{bL}$$
In short, MRTS is a similar concept to MRS, but in the output aspect.