Insights about US Deficits and the Impact on Bond Yields
Facts
- Trump Administration is widely seen as likely to increase or maintain high fiscal deficits.
-
To assess the impact of large deficits on yields, it is important to look at the total debt in the economy,
not just government debt.What matters for markets and the economy is how much collective new credit is being created, and the incentive and desire of investors to buy it.
-
Debt Supply & Demand amount would flow to Rate. If government spending increases, then it means debt supply increases (there would be more borrowing), pushing up rate to increase.
High Borrowing -> High Rate -> Depressed the private borrowing.
Low/Normal level of credit creation would otherwise drive down inflation.
Two Cases:
-
Bad Scenario: Push up Inflation.
Total Debt/GDP increase (private and public debt / GDP) increase && Currency Weaken. Then Yield Curve would steepen, derived by long term rate increase, as nobody purchase the long term bond.
Think about a graph with x-axis (term), y-axis (yield), and a upward sloping curve.
Yield curve steepens.
-
Good Scenario (now the US situation): Do not drive up Inflation
Under this case, no buyers are buying the long-term debts.
Total Debt/GDP increases, but yield curve is flat. Public squeezes private investment. The increase in public debt does not increase private borrowing, so no extra purchasing resulted from households. Help relieve the inflation.
Yield curve flattens.
-
Example:
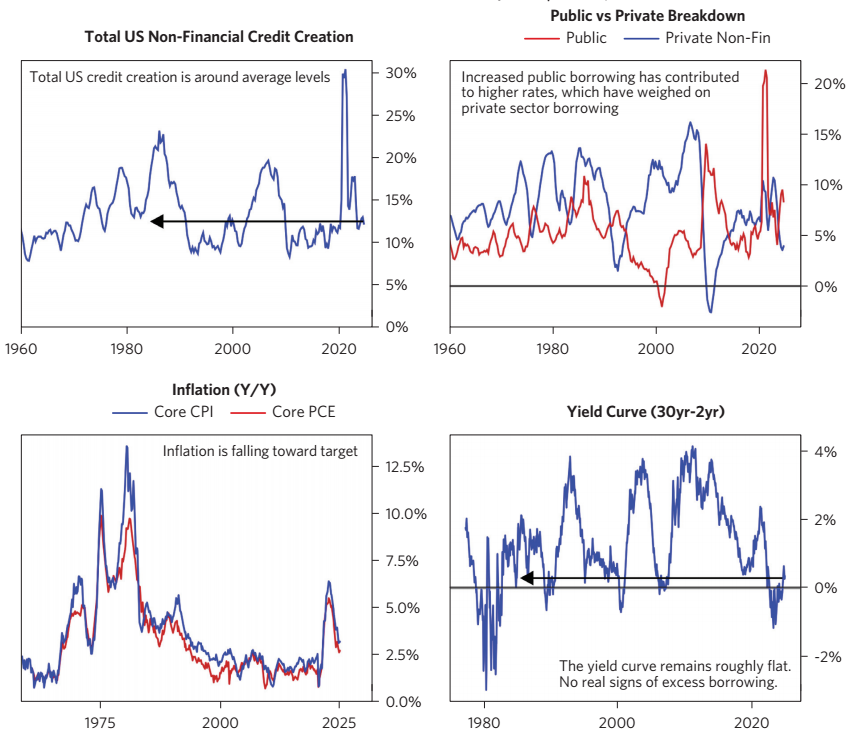
Now is the Good Scenario: The top-left figure shows the current credit creation in US is under normal level. Top-right figure shows that Public and Private debts are negative correlated. Public squeezes private, so total debt did not get up too much high.
1980s: Top-left figure shows total debts went high; Top-right figure shows public and private were positively correlated. So, bottom-left figure shows inflation hikes.
Bottom-right figure shows implicitly that the current long minus short term rate is at low level, imply that the yield curve is flat, consistent with our Good/Bad Scenario Rationale.
Supply & Supply Side of Debts
-
Supply Side: Currently, there are high public borrowing, and low private borrowing.
-
Demand Side:
Due to previous QE, Debt yield is high for investors => that would be attractive to un-levered investors, because Debts still bring enough return and less risks, attractive to people.
However, the levered investors fact different situation. As they hold debts already, high debt rate would become both their costs and returns.
-
The current real yield is about 2% in US, which is high relative to much of the rest of developed world. US nominal yields are at levels where the yield is attractive and diversifying relative to stocks allocation for those who need to supplement debts into their portfolio.

Again, the current yield curve is flat. For leveraged investors, they have debts liability already. Returns and Costs of debts offset.
Reference
Bridge-Water
Our Thoughts on Large US Deficits and Their Impact on Bond Yields
Market Timing
Allocating assets into different asset classes may depend on the (1) risk aversion, (2) time horizon, (3) tax status. And the (4) market timing also matters.
In other words, sensing the market timing would help you
- allocate assets into different asset classes such as debts, equity;
- be out of the market in the bad months, and get into the mkt in the good period.
Cost of Market Timing
- Out at the wrong time. Miss the opportunity of growth, i.e..
- Transaction Costs
- Taxes
Market Timing Approaches
Non-financial indicators
- Spurious indicators that may seem to be correlated with the market but have no rational basis.
- Though there is no reasoning, there may still have some statistical pattern. Do not ignore it.
- Those indicators give a sense of direction.
- Feel good indicators that measure how happy investors are feeling – presumably, happier individuals will bid up higher stock prices.
- The problem is that those indicators provide contemporaneous or lagging status of the market, may lack of predictability compared with the leading indicators.
- Hype indicators.
- Still the contemporaneous problem. Those factors tell the correlation right now, but do not have predictive power.
- Also, the abnormality can be tricky when the environment is shifting.
- Technical indicators, such as price charts and trading volume.
- Past prices (such as price reversals or momentum, January Indicator)
Hard to say the momentum or the reversal could stay for years.
- Trading Volume & Money Flow
-
Price increases that occur without much trading volume are viewed as less likely to carry over.
- And, very heavy trading volume can also indicate the turning points in the markets.
-
The money flow is the difference between uptick volume and downtick volume. People find there are some predictability for longer periods, in that the equity markets overall show momentum.
-
Market Volatility
-
Empirical research finds some evidence between the volatility change and returns.
-
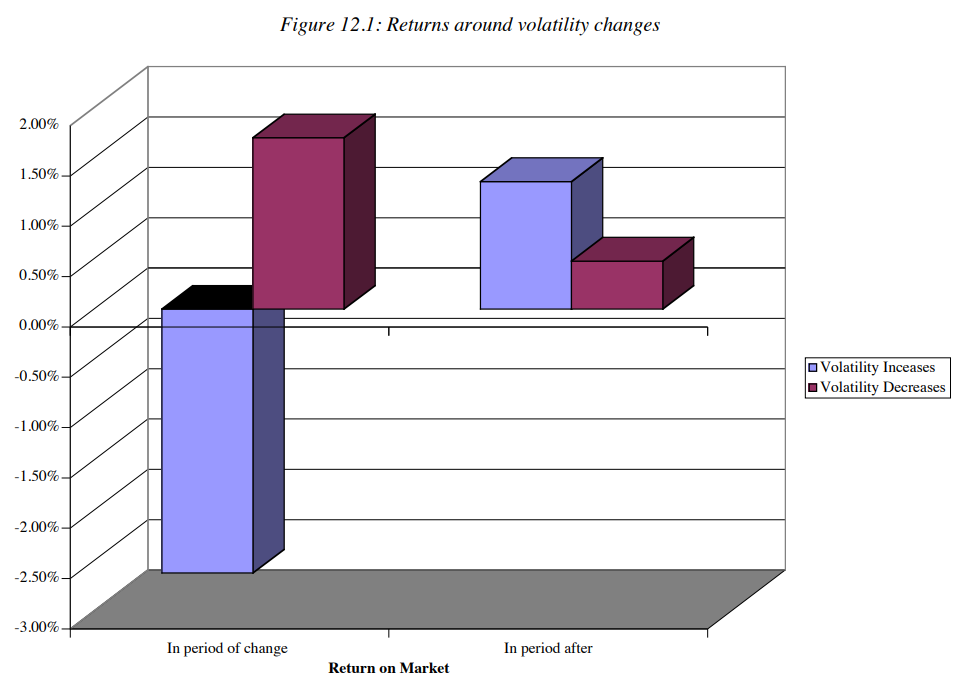
See the blue bar: In periods that volatility increase and the market return goes down. After that period, the market is predicted to be like volatility increase and market return goes up.
-
Purple bar: in periods of volatility decrease and market return increase, the following period may have less volatility decrease and still returns.
-
Other price and sentiment indicators
-
Chart Patterns: supports and resistance lines are used to determine when to move in and out of individual stocks.
- Sentiment indicators: measure the mood of the market.
- Trader sentiments
Mean Reversion indicators, where stocks and bonds are viewed as mis-priced if they trade outside what is viewed as a normal range.
That approach is based on the assumption that stock price would revert to the P/E, and debt return would revert back certain interest rate.
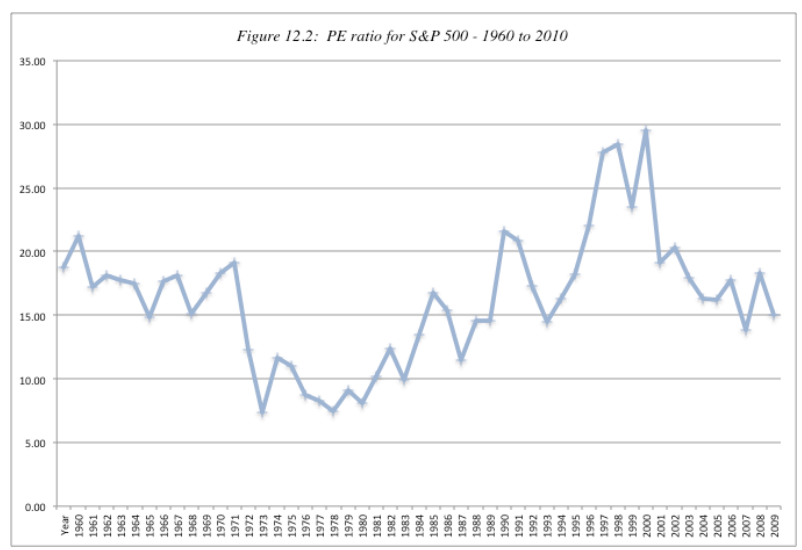
- P/E (see figure below for the normal range of P/E ratio)
If stock is above or below the normal P/E, then it is overvalued or undervalued. The median is around 16.
The P/E might go abnormally high in recession, not only because (1) the stocks are overvalued, but also because (2) the earnings are dropped down during recession.
-
Rate performs similarly.
\Delta Interest Rate_t = 0.0139 – 0.1456 InterestRate_{t-1}, where R^2=0.728. Coefficients are significant.
The regression suggest two things:
- Change in interest rates in the period is negatively correlated with the level of rates at the end of each prior year.
- The speed shrinks. For every 1% increase in the level of current rate, the expected drop in interest rate in the next periods increases by 0.1456%.
Fundamentals
Using the fundamentals to predict market timing is to focus on macroeconomic variables such as interest rate, inflation and GNP growth and devise investing rules based upon the levels or changes in macro economic variables.
Two keys of using this approach. (to build up the logic chain of prediction)
- Get handle how the market reacts as macro econ fundamentals change.
- Get good predictions of changes in macro econ fundamentals.
- Macro economic variables, such as the level of interest rate or the state of the econ cycle.
There are some common sense that the following changes would indicate the increase in stock price:
- Buy when Treasury bill rates are low, will end up with growth of stock price.
- Buy when Treasury bond rates have dropped, will end up with growth of stock price.
- Buy GNP growth is strong, will end up with growth of stock price.
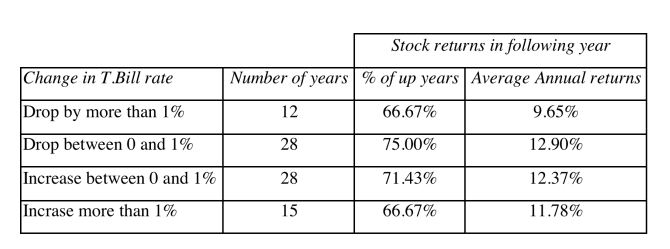
However, empirical evidence shows the other way. For example, the table below shows T-bill rate drops or increases could both contribute to the increase in Annual returns.
Valuing the Market
Just as you can value individual stocks with intrinsic valuation (DCF) models and relative valuation (multiples) models, you can value the market as well. If the valuation is faithful, you can reply on it to predict the market timing.
- Intrinsic valuation that apply to the mkt. <- depends on assumptions and inputs.
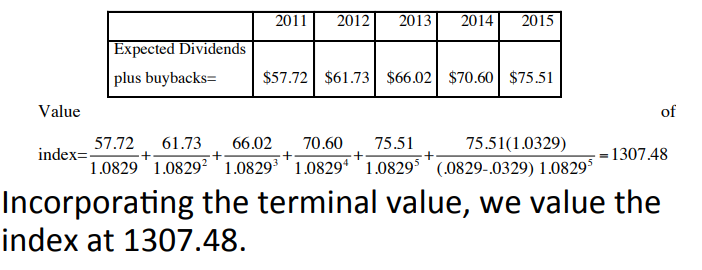
Use the S&P500 price and the index’s dividends to do the DCF.
INPUTs: (1) S&P500 price, 1257.64 at 2011(2) Dividends and buyback on the index amount over previous year, 53.96 (3) expected earning growth for the following 5 years, 6.95% (4) expected growth of the economy (set as risk free rate) 3.29%, (5) treasury bond rate, plus the market risk premium (set it yourself) 5% to get the cost of equity 3.29%+5%=8.29%. Then, do the DCF
-
Relative Valuation <- value a market relative to other market, or across years.
-
Other methods, such as run regression on P/E to T-bill to find correlation.
Does the Market Timing Work?
-
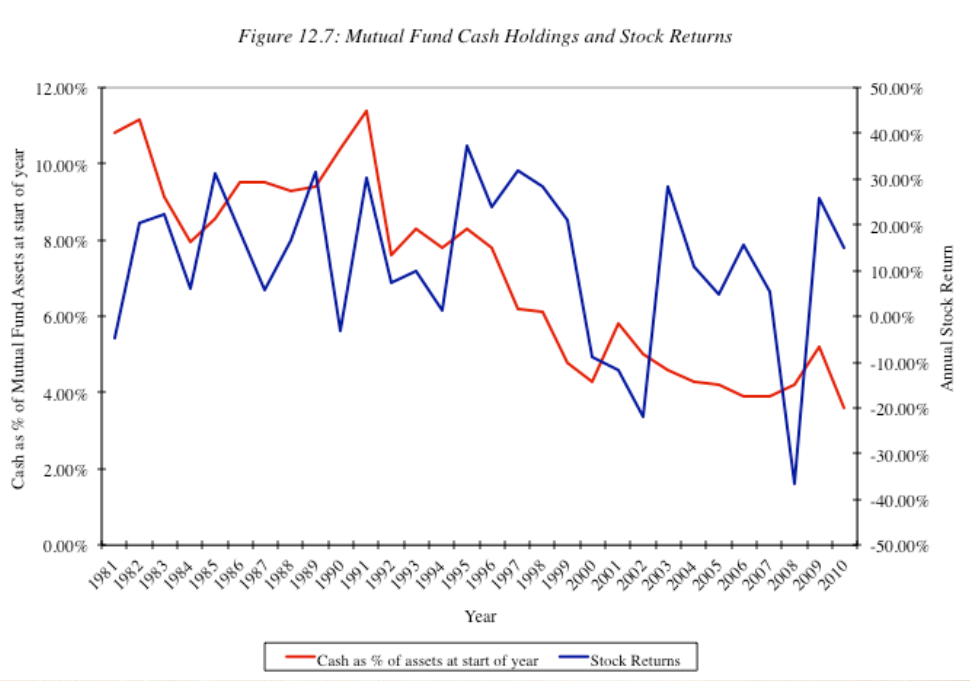
Mutual Fund Managers: constantly try to time the markets by changing the amount of cash that they hold in the fund. If expected bullish, then cash balances decreases, vice versa.
They call timing the market as Tactical Asset Allocation, TAA.
See figure below, empirical evidence shows they do predict the market by changing the cash position.
-
Investment Newsletter: often take bullish or bearish view about the market.
There is continuity on Newsletter way. Investment newsletters that give bad advice on market timing are more likely to continue to give bad advice than are newsletters that gave good advice to continue giving good advice. In other words, it depend on the writer’s ability.
-
Market strategists: make forecast for the overall market.
-
Professor Market Timers provide advice, however, their decision works for very short time, and only work for private clients.
Market Timing Strategies
- Adjust Asset Allocation: change across asset classes
- Switch Investment Styles: change within asset classes but different styles, such as from growth to value.
- Sector Rotation: with in asset classes, but different sector.
- Market Speculation.
Market Timing Instruments
- Futures Contracts
- Options Contracts
- ETFs
Implications and Insights
Overall, it’s good summary and a Beginner’s Tutorial, but not include technical implementation method, instruction, or philosophy.
Do provide some inspirations.
Reference
https://pages.stern.nyu.edu/~adamodar/New_Home_Page/webcastinvphil.htm
债券的分析框架
债券利率波动存在上下限区间
- 上限:实体部门的投资回报率,ROIC (return on invested capital)。因为上市公司ROIC要超过债券的利率,企业才有可能借债,不然承担不了利息成本
- 行业的负债水平与ROIC呈负相关,因为负债越高,投资回报率倾向于越低
- 高负债行业对债券市场影响大,因为规模大。
- 下限:刚性融资需求的利率水平,主要包括:城投 & 地产
- 城投代表地方政府的隐性担保,相当于信用高,风险低,因此利率低。
- 刚需融资需求萎缩,会拉低利率,因此利率下限降低
当前债券市场的特征
长短期利率脱钩,当前处于bull flat的情况
- Bull Flat 意味着:长期利率降低,长期债价格上升,短期相对不变,整个收益率曲线goes flatter
- Theoretically, 短端利率的波动大,且响应速度快。但当前短期利率没有明显变化,意味着市场对短期政策力度预期低,因此不投向短期。
后续债券市场的展望
- 方向(按照2025年利率上下限变动趋势来预测2025年利率的变动)
上限:拆分ROIC贡献的主要行业,2024年为光伏和电力等,2025年预计两行业增长有限,得有新兴产业才能支撑ROIC增长。ROIC预期不提升,因为没有增长机会;
下限:此前有刚性融资需求的城投债 & 地产拉跨,需求少,需要有新的刚性融资需求的部门增加才能推动利率下限上升。当前城投债预期也不提升,因为没有新的基建项目和空间,房地产也拉跨,因此没有需求。
总之,若无新的增长点,上下限方向均向下。
-
空间
-
当下房租(租金回报率)和按揭还款(融资成本)倒挂明显。未来有趋近的空间,因此有余地。
-
假设明年CPI回到1.5%,PPI回到0%,用贷款利率减去CPI和PPI的均值为实际利率。用此实际利率与历史对比,也仅处于中性水平。画外音,明年CPI大概率回不到1.5%,可能更低,因此明年实际利率更高,无法刺激经济。所以还有更多的降息空间。
- 此外,今年存贷款利率下调幅度多于货币市场资金成本(货币市场投资or理财收益更高),所以存款从银行表内向外转移。因为货币市场投资主要投向债等,这意味着短期债的收益高于存款利率,因此CB还有执行Open Market Operation,降息的空间。
- 节奏
-
利率走势和很多宏观指标脱钩,因为宏观统计数据失真(高估),无法反应真实情况,而利率作为市场真正交易的产品,能更好的反映市场的真实情况,因此存在利率与其他指标脱钩的情况。
-
目前,还有一个指标,企业信贷规模变化,与利率还有显著的相关性。因此可以通过推断企业信贷的供求端,即信贷供给&企业杠杆率,来推断利率变化的节奏。
-
化债or信用的周期:第一阶段,通过密集的发行新债券,置换旧债券,拉动社融增速,因为有新债券发行,对资金需求高,短期利率推高;第二阶段,逐步偿还新债券,在债务偿还过程中,信贷会收缩,利率逐步下降;第三阶段,债还接近尾声期,信贷增速和杠杆率将降到低位,利率降至低点。后续才会重启宽信用的周期。
目前还处于第一阶段,新债券集中发行会推高利率。
即使目前经济政策是降利率,但是与信贷周期短期推高利率叠加,可能导致2025年上半年(化债or信用周期的第一阶段),整体利率下降不明显,因为政策的降利率和信贷周期的升利率对冲了一部分。后半年利率会逐步下行。
但具体也要看OMO的力度。
Be careful if they Talked the Talk, Walked the walk, disappointing the mkt and people again and again.
Reference
https://www.bilibili.com/video/BV16ViRYJEY8/
关于中国经济现在 – 付鹏在汇丰的报告
当前经济模式从增长转为分配
当前经济模式由增长(把蛋糕做大),变为分配(把蛋糕切好)。参考日本的1980s后的状况,经济没有增长并不意味人均变差了或者人不幸福了(日本消失的40年),同时而经济增长也不意味着人均都增长了(近年我国的增长模式)。
如何应对
当前上述由增长转为分配的背景下,普通人需要做的是,参与到到分蛋糕的过程中,参与分配,而不是参与增长。But how to do it?
- 离权力近一点,离资源近一点,就能多吃一点。
- 而卖劳动力(按以前增长的模式挣钱),就只能少吃一点。
日本低利率时代,巴菲特carry trade,在日本发日元债,以低利率(低成本)借钱,然后直接投资日本公司。In other words, 巴菲特参与了日本过去40年的存量财富分配。
当前经济困境
经济流转的过程,一方的消费是另一方的收入。然而消费和收入流转需要时间。
- 当经济扩张时:富人先进五星级酒店,富人先买超跑,富人先吃海鲜,然后逐步下沉,到最后是老百姓吃上海鲜,老百姓开上汽车,老百姓进五星级酒店。
- 当经济收缩时,却是相反的:先收缩的是底层。网约车司机、快递员、外卖小哥等是对经济需求反馈最快的。而坐办公室的往往反馈很慢,要等年终降薪、发不出工资、裁员等才会有反馈。同时,近年网约车司机数量剧增并不是因为农村劳动力进城,更多的是,中产阶级的陨落。只不过是你的阶层不一样,你看的问题不一样。
- 从经济数据反馈,经济收缩的时候是底层先吃苦,往往一定周期后才能传递到经济数据上,因此宏观经济指标的反馈将滞后。
经济数据不真实,实际情况是通缩,没有增长。
主要原因是人口问题,老龄化及劳动人口缩减。
刺激经济的方式
关于说法“内债不是债”。诚然不同于外债需要用外汇还,有本币的国家可以通过印钱来还债,但是长期以往会导致流通中的货币增加,产生潜在通胀问题(可能当前短期通缩,因为没有过量现金流通,但货币总量增加了,长期一定会有通胀风险)。
国家政府需要长期稳定就需要保持Public Sector的平衡。债务增加需要靠(1)借新还旧(2)提升税收还。
- 税收收入 = 税基 * 税率
- 税基 = f(人口,收入,消费意向, etc)
- 税收收入 = f(人口,收入) * 税率
- 当前总人口少了,只有增加收入,或者增加税率,才能满足债务增加。
此前,公共部门的债,企业债,可以通过供给侧改革&房地产等方式输出给私人部门,换句话说是将企业和政府债转移,由老百姓买单。但当前,人口结构和人口总量不一样了。当前供给过剩,及需求不足同时存在,导致价格(PPI,CPI)一降再降。
房地产市场
房价在2008年-2015年第一波上涨,而2015年-19年才是上涨幅度最大的,此阶段也是80s后需求最旺盛的年代。然而收入增长并没有房价增长快,房价是由需求推动的,而非购买力。北京的房价收入比是世界最高的一批。
买房的时候抵押贷款,相当于把自己的未来收入折现抵押给银行,买房。房子此后换手,如200万买了卖400万,相当于把债务转移给接手人,由其未来现金流折现来偿还。所以房价上涨,而收入未上涨,相当于掏空年轻人或者中年人更多年的未来收入。
如果收入不增长,那么实际各种交易都是在做资源分配,而非增长。一批人的财富来自于另一批人的债务,如上文200万房卖400万的例子。但如果没有更多的年轻人愿意买房了,400万的房卖出600万了,相当于旁氏骗局的链条断了,比较收入没有实际增长。
而房价在整个经济体中有着重要的意义,关联着抵押和债务。如果房价降,相当于资产降,而债务不变,只能equity降低(相当于wealth降低),如果equity降到0或为负,则资不抵债。
放大到宏观,纵向,收入上涨才能保证房地产的需求和价格。而收入可以理解为未来现金流折现,未来年轻人的收入折现。如果年轻人少了,相当于能折现的收入少了,房价难免下跌。年轻人把房子买走了,让中老年或者少数人(如房地产开发)获得了财富,但是年轻人获得了负债。
未来消费结构
当前人口少了,人口结构变了,老年人成为了消费的主导(尹瑞哲的报告,年轻人少的省份消费能力强),同时中长期看,消费的结构向年轻人的方向转变
中国企业周期
中国可以用很短的时间将产业链做到“全球遥遥领先”,在政策的保护期,PPI为正,企业都可以活,但同时由于有利润空间,企业进入市场,会造成很多同类竞争。但一旦保护期一到,到市场经济竞争的情况下,企业开始打价格战,开始PK、竞争、内卷,PPI开始转负。然后一轮产业过剩,开始淘汰。
政府驱动再引导新的产业。用这种前浪推后浪的方式,推动整个产业各个环节的周期缩短到五年,但是代价就是很多行业会以很快的速度进入到PPI为负,而所有能到PPI为负的产业,最后能活下来都得感谢有自己的负债端,有居民部门能买单。一旦内需不足,居民部门不再为企业负债买单(或者无法买单,因为经济压力自底层向上传导),就会出危机,就是当前经济现状。
所以看产业链成熟度,或者说看周期投资时,不能等产业已进入竞争模式的时候投(如新能源),因为在价格战,博弈分蛋糕,就像抽签众多企业中能成活的一个(当然也不要买行业ETF,而如果一定要投此行业,投最有机会活下来的,负债端压力小的,有打价格战空间的)。要在政策利好的时候投,因为在把蛋糕做大,有政策保护。
投资是看预期,不是现状。
供给侧改革
中国供给侧改革的起点是2002年,PPI为正,核心CPI为正,有效需求为正。持续到2012年,供给开始过剩,但有效需求可以继续加杠杆(相当于居民部门用负债端扩大的方式支撑供给侧扩张),但供给矛盾已经产生,2009年供需双落,这就是中国这一轮从2012年开始的大周期的末端。
此处时间有点混乱,付鹏建议看《朱镕基总理答记者问》,三卷本。
“只要人还在,啥债都能化”。只要人不在,这债怎么化?税率。量收不上来,就抓率。
财政、利率、汇率传导
当财政需要扩张,利率下降,财政花钱短期内不会流转到居民部门,国内经济的有效需求不够,储蓄过剩,投资回报率下降,利率下降。
在这种背景下,汇率就代表着你的实际回报率以及本币购买力,是减弱的,本币贬值。
日本长期低利率,而同时保证汇率稳定的原因。理论上将,利率差会导致汇率差,但日元此前相对稳定。原因是日本进行carry trade,大企业(三井、三菱etc)低息借日元然后买海外资产。用海外资产来支撑日元汇率。然而企业通过carry trade挣了钱,老百姓无法进行此操作(其实老百姓也可以买海外股票,但是大多数老百姓没有这么做),老百姓穷了(收入降低无法支撑消费)所以日元的稳定才难以维持。
Implications
当前两会提出财政和货币双重宽松,希推高国内CPI避免通缩,短期市场可能会利好,因为投资者不希望踏空,且不希望被通胀影响。但交易上可能只有短期影响,因为债务需要用税收买单,宏观经济的核心问题(人口)并没有解决,且没有新的技术能推动经济增长,那么中长期就难以维系。
交易上可能短期实现收益后投资海外资产比较好。
Others
- 投资方向,中产面临巨大困境,做高端(爱马仕),做低端(拼多多。放弃中端(LV,Chanel,Prada)
- 消费模式类似,只有老人的消费和年轻人的消费可以做,中年人的消费能力降低。
- 投资产业要投早期的产业,已经成熟的只能投负债端优秀的或有价格战能力的。
Reference
https://www.wenxuecity.com/news/2024/12/02/125897172.html
美元循环视角下的特朗普政策
我们假设以下模型:
- 美国付美元买商品(净进口 Import > Export)。美元流出,商品净流入。
- 美政府发美元债,各国资金换美元买美债。美元净流入,形成债务。
此时如果剔除上述流程中美元最为交易媒介的职能,相当于:美国发美债,净买入全世界的商品。
此模型(以下简称”双赤字+强美元“)代表了近年来美国国际贸易的流转模式。
1944-1973:布雷顿森林体系
二战末期,布雷顿森林体系建立(”美元以黄金背书“的模式)。此时美推出马歇尔计划,向欧洲各国提出援助以支持其重建。计划开展过程中,欧洲重建消化了美国的过剩产能。
然而特里芬难题预示着布雷顿森林体系的瓦解,也的确,美长期国际收支逆差,黄金储备无法支持美元的兑换。
特里芬难题(Triffin Dilemma),由经济学家Robert Triffin于1060年提出。该理论说明:当一个国家的货币同时作为国际储备货币时,有可能造成国内短期经济目标和国际长期经济目标的利益冲突。当外国想持有该国货币(全球储备货币)时,该国必须愿意提供额外货币供应,以满足世界对于这个“储备”货币的需求(外汇储备),从而导致贸易赤字。
如:使用国家的货币(如美元)作为全球储备货币,导致国家的货币政策和全球货币政策之间的紧张关系。这反映在根本的国际收支失衡,特别是经常收支:有些目标需要美元总体流出美国,而有些则需要美元总体流入美国。同等程度的货币流入和流出不能同时发生。
1980s 里根大循环
1980s,美经济强劲。时任总统里根当选并主张”双赤字+强美元“的模式,该模式指:财政和贸易双赤字,提升利率保证强美元。
- 财政赤字意味着花费大于税收,额外的花销需要发美债融资。外国买美债,将美元输入回美国。
- 贸易赤字代表美国进口大于出口,买全世界的货,付美元,将美元输向外国。
- 两赤字通过美元流转,一进一出。两个赤字模式互相增强。且此模式保证美元流转,市场上美元多余的美元,并没有导致通胀。
但是此模式面临的巨大问题在于:
- 美通过借新还旧维持高额的债务存量,相当于巨型旁氏骗局,模式是否可持续难以预测。
- 该模式依赖美元的信用作为担保,逆全球化可能削弱全球对美元的依赖度。同时,俄乌战争等地缘冲突可能加大局部风险,降低各国对持有美债作为资产的需求,转而投向黄金等。
特朗普2.0时代的“新循环”
三层逻辑:
- 特朗普竞选宣言中一部分为增加关税,减少公司税,此政策为保证美本国产业链生产力。但关税政策会阻碍进口,减少外国对美贸易输入,使外国美元收入减少。离岸美元量减少。此时,若外国仍对美元需求旺盛,将推动美元升值。
-
$Y=C+I+G+NX$,
$Y-C = (I+G)+NX$
LHS 是私人部门盈余,RHS I+G是政府赤字,NX是外国部门盈余
对外关税会减少进口,NX增加;对内减税会增加投资 I 增加。最终导致LHS 私人部门盈余增加,利好Equity Mkt.
-
结合此前Blog的分析,特朗普竞选计划可能会推高通胀,同时增加财政赤字,此行为与Fed当前认为通胀下降,降息实行软着陆的预期不符,因此可能Fed减缓降息。
同时,Bessent 被选为特朗普第二任任期的财长,其主张3-3-3 plan,即3%增长,3%财政赤字,300 million barrel crude oil。Bessent财政赤字收缩的目标看似与特朗普竞选战略相悖,但历史上”里根大循环“时期,消费高涨的前提保障了降低税率但提升税收总额的可能性,即随税率降低,但刺激消费、扩大税基,消费总额上升带来总税收上升。
因此,特朗普降低贸易赤字,及Bessent降低财政赤字的策略合力,形成了”降双赤字“的模式,该模式依然自洽,能维系美经济循环,且降低了引用为美元背书的依赖。
Implication
初期:
- 美政策直接利好equity mkt,因为减税直接提升企业净利润。
-
关税增加会使美贸易受阻,叠加减少移民等政策可能推高工资、物价等,通胀难以降低,因此Fed降利率预期推迟。
美元指数因此维持高位。黄金降价,因为与美元逆相关。
中期:
随着经济企稳,物价降低,财政赤字降低,Fed重启cut interest。此时美元贬值,黄金走强。
Impacts of Trump’s Strategy on Trading
- FX: The impacts on US dollar are complicated. On one hand, the US economy is underwent rate cut before the election, aiming to help the economic growth. On the other hand, Trump’s policy (high tariffs and inflationary wages policies) would result in higher inflation, so that Fed might be pressure to rise rate against the greater price increase. The US dollar index would be largely affected by the above mentioned polices.
Trump states that the US trade deficits have reached to over $1 trillion, implying the imbalance trade condition. The monetary department (Fed) might depreciate US dollar, through which US exports might be accelerated. To make US dollar depreciate, FFR might go downward.
However, The independence of Fed matters. As Fed’s goal might diverge from Trump’s policy, Jerome Powell’s insight of fighting inflation might not be coincident with the campaign strategy. If wages rise, pushing up inflation, Fed would increase rate again.
In sum, there is an uncertainty on FX changes. The majority of the market consider Trump’s policy would outperform, so USD appreciates after election.
-
Commodity:
- Gold: As USD appreciates, gold price decrease.
- Metals: Coppers might experience uncertainty. USD appreciates, commodity price shall decrease. However, the infrastructure plan increase the demand of related commodities as well such as coppers. Thus, the price change of coppers are uncertain.
- Energies: similar to metals. Two-way effects.
- Cryptos: Simple logic. Boosting cryptos.
-
Stocks: tax cuts definitely benefit firms. Stock price raises.
- Bonds: money flows to stocks, less demand on bonds. Thus, bond price decreases, and yield increases.
About Trump’s Campaign Statement
- Seal the border and stop the migrant invasion
- Carry out the largest deportation operation in American history
- End inflation, and make America affordable again
- Make America the dominant energy producer in the world, by far!
- Stop outsourcing, and turn the United States into a manufacturing superpower
- Large tax cuts for workers, and no tax on tips!
- Defend our constitution, our bill of rights, and our fundamental freedoms, including freedom of speech, freedom of religion, and the right to keep and bear arms
- Prevent world war three, restore peace in Europe and in the middle east, and build a great iron dome missile defense shield over our entire country — all made in America
- End the weaponization of government against the American people
- Stop the migrant crime epidemic, demolish the foreign drug cartels, crush gang violence, and lock up violent offenders
- Rebuild our cities, including Washington DC, making them safe, clean, and beautiful again.
- Strengthen and modernize our military, making it, without question, the strongest and most powerful in the world
- Keep the U.S. dollar as the world’s reserve currency
- Fight for and protect social security and Medicare with no cuts, including no changes to the retirement age
- Cancel the and cut costly and burdensome regulations
- Cut federal funding for any school pushing critical race theory, radical gender ideology, and other inappropriate racial, sexual, or political content on our children
- Keep men out of women’s sports
- Deport pro-hamas radicals and make our college campuses safe and patriotic again
- Secure our elections, including same day voting, voter identification, paper ballots, and proof of citizenship
- Unite our country by bringing it to new and record levels of success
The above 20 statements are listed in Trump’s Republican Party’s Website, https://www.donaldjtrump.com/platform. Combining with the Table of Content, here are some assessments.
| Table of Content | Campaign Statements | Implication |
|---|---|---|
| CHAPTER ONE: DEFEAT INFLATION AND QUICKLY BRING DOWN ALL PRICES | Defeat inflation, Unleash American Energy | Trump plans to lifting restriction on Energy Production, and terminate the Green New Deal, continuing the usage of low cost energies such as oil, natural gas, and coal. US has turn from the largest Oil importer to Oil exporter, and Trump will extend this road. This policy would affect the oil price, the status of US dollar, and the commodities price, and further cooperation agreements. |
| CHAPTER TWO: SEAL THE BORDER, AND STOP THE MIGRANT INVASION | Stop Immigrants | Reduce labour supply, potentially pushing up wages. Might be harmful to inflation. |
| CHAPTER THREE: BUILD THE GREATEST ECONOMY IN HISTORY | Tax Cuts; Support using Crypto and AI | Prioritising American producers over foreign outsourcers. De-globalisation, increase production cost, but help resolve employment problems. Stabilise the social development. Support using Crypto and AI innovation. |
| CHAPTER FOUR: BRING BACK THE AMERICAN DREAM AND MAKE IT AFFORDABLE AGAIN FOR FAMILIES, YOUNG PEOPLE, AND EVERYONE | Stabilise housing price; accessible education; affordable healthcare | Social Stability, making welfare available for people. |
| CHAPTER FIVE: PROTECT AMERICAN WORKERS AND FARMERS FROM UNFAIR TRADE | Higher Tariff; stop outsourcing; save Auto Industry; reduce trade deficit | Place higher tariffs, protect US industries and manufacturing powers. Save Traditional Auto industries, cancel supports to EV. Trade independence from China, including vehicles imports. Keep supply chain, and maintain internal economic cycle. |
| CHAPTER SIX: PROTECT SENIORS | Medicare, Social Security, Cares for Seniors. | Social Welfare. Same as CHAPTER 4. |
| CHAPTER SEVEN: CULTIVATE GREAT K-12 SCHOOLS LEADING TO GREAT JOBS AND GREAT LIVES FOR YOUNG PEOPLE | Children; Teachers; Schools; Knowledge; Gender Indoctrination | Social Welfare. Similar to CHAPTER 4. Adding the gender things. |
| CHAPTER EIGHT: BRING COMMON SENSE TO GOVERNMENT AND RENEW THE PILLARS OF AMERICAN CIVILIZATION. | Rebuild Cities | Infrastructure Construction |
| CHAPTER NINE: GOVERNMENT OF, BY, AND FOR THE PEOPLE | – | – |
| CHAPTER TEN: RETURN TO PEACE THROUGH STRENGTH | – | – |
Trump’s campaign strategies seem self-containing.
- Fiscal Revenue and Expenditure Balance: In most of case, fiscal expenditure need to be supported by fiscal revenues. Both (1) the reduction of corporate tax, (2) the increase in infrastructure construction, and (3) upgraded social welfare would be financed by increase in Tariffs.
However, to what degree the revenue could cover the expenditure might need specific clauses of policies to be confirm and need further evaluation of the post-policy impact.
-
Labour Market Implication: Stop immigrant would reduce the labour supply. However, Trump’s strategies aim to remain the manufacturing power insider the U.S.. Stop outsourcing and keep the supply chain in America would provide job opportunities, increasing the employment demand. Those policies together would increase the employment level and be helpful for the social stability.
-
Inflation: Oil supply increase would decrease commodity price, relieving inflation. Labour market actions (stop immigrant and outsourcing, increase wages) would increase inflation. Hard to say the inflation would go upward or downward.
-
International trade: Policies would downgrade the globalisation. Definitely harmful to all exporting countries. Exporters might need to find other large goods importers, or need to consume the excess supply power themselves. However, not just America, but the EU are all implement tariff protection, keep the pricing and competitive advantages to the local companies.
Theoretically, de-globalisation/trade protection would harm the economic efficiency as relevant parties did not implement the comparative advantage. However, US, as the largest importers, would actually extract productions from others, and take the benefits from the trade protection. In addition, US decides to contain the manufacture power, and exports its production
Recent Insights of Trump Trade
Trump Trade is tied with Trump’s policy, and the potential of Trump’s victory.
Trump’s policy is likely to result in higher inflation (as he advocates high tariffs, low tax, looser fiscal). The Fed is expected to react to the increase in inflation by raising EFFR. Therefore, the US Dollar Index is expected to increase, based on the Trump trade and so on policies. Trump’s website illustrates polices such as Tax Cuts, Trade Protect to remain manufacturing power in the US. This year, there are people predicting that the Fed might not react by increasing interest rate, but the MoTreasury might react by increase the fiscal deficits.
Based on Trump’s previous policy in 2018, he loosened bank regulation and capital requirements. Leave the Paris Agreement and cut green energy that reduces the manufacturing efficiency. Related industries might be affected. For instance, Banking and Financial industries and Crude Oil related commodities might be accelerated, but Green Energy Industries might be less considered. Also, lower corporate tax, higher earnings per share equals higher stock market. Cryptos, through usually experiences the similar moves as Gold, might increase, because of the support from Elon Mask.
In sum, With the Trump Trade, the inflation is expected to increase, so the Fed or MoTreasury react by increasing FFR. Subsequently,
– US dollar index is expected to increase (as rate increase),
– Gold and Crude Oil are expected to decrease (as USD appreciate, rate increase, and debt increase), and
– US Stock price increase (and US corporates benefit from tax cut), and
– Cryptos increase (because of the support of Elon Mask, however there is downside power on it),
– Debt price is expected to decrease, yield increase (as FFR increase target rate).
End.
The Fine Art of Small Talk
by Debra Fine
A book that teach you how to overcome the fear of start a conversation, and how to delicately continue the talk, making others comfortable.
1. What’s the Big Deal about Small Talk
We become better conversationalists when we employ two primary objectives.
- Take the risk, starting a conversation with a stranger.
- Assume the burden. It’s our responsibility to come up with topics to discuss, to remember people’s name and to introduce them to others, to relive the awkward moments or fill the pregnant pause.
2. Get over Your Mum’s Good Intentions.
- In safe situations, make it a point to talk to strangers. Start it!
To expand your circle of friends and colleagues, you must start engaging strangers and acquaintances in conversation. There is no other way. Strangers have the potential to become good friends, long-term clients, valued associates, and bridges to new experiences and other people. Start thinking of strangers as people who can bring new dimensions to your life, not as persons to be feared.
-
Introduce yourself.
People expect you to mingle on your own, introduce yourself, and take the initiative to get acquainted.
-
Silence is impolite
Start to talk, silence is not golden.
Don’t risk being taken as haughty or pretentious by keeping silent; it can cost you dearly. Start small talking and let others see your personality. You know how much you appreciate the efforts others put forth in conversation. Make the same effort. Contrary to what your elders taught you, silence is not golden.
-
Good things come to those who go get them!
Don’t spend another minute thinking that if you just keep waiting, interesting people will introduce themselves.
We end up paying twenty pounds to attend an event and then seek out people we already know because it’s less threatening. Yet the purpose of the event was to make new contracts.
-
It’s up to you to start a conversation
When you walk into a luncheon or a cocktail party, more people there are scared to death to talk to you. Fear of rejection keeps many of us from risking conversation, but the probability of rejection is actually quite small.
You will be the hero if you start the conversation. You will gain stature, respect, and rapport if you can get the conversation going.
-
It’s up to you to assume the burden of conversation
You cannot rely on the other person to carry the conversation for you. One-word answers to questions do not count as shouldering your share of the burden.
To become a great conversationalist becoming invested in the conversation and actively working to help the other person feel comfortable.
Ask icebreaker questions. Such as “What do you do for a living?”
3. Take the plunge: Start a conversation!
When someone gives you a smile, you are naturally inclined to smile back. Be the first to smile and greet another person. Just a smile and a few words, and it’s done. Be sure that you make eye contact. That simple act is the beginning of establishing rapport.
Mingle with the people in the audience, making a personal connection with as many as possible.
The best way to get people comfortable enough to open up and express themselves was to look them in the eye and ask “What’s your name?” Making eye contact and placing the emphasis on the word your, rather than the word “name”, signaled to the person that they were important.
- What’s in a name?
Learning and using names is probably the single most important rule of good conversation.
Focus on the name, repeat it, and then formulate your answer.
Don’t go through the while conversation pretending you know the person’s name. Say something like “Excuse me, I’m not sure I got your name”. It’s always preferable to have the other party repeat it than to fake it. Never, ever fake it!
Individuals with foreign or unusual names get slighted more than the rest of us. Make it a point to learn the proper pronunciation, even if it means that the other person repeats it a few times.
Learning names is part of hosting the conversation. A host is always expected to know and use every person’s name, since the host is responsible for making introductions as new individuals enter the conversation.
Acting as the host puts everyone at ease and creates an atmosphere of warmth and appreciation that naturally encourages conversation. It also positions you as a leader in the group.
-
It’s better to give than to receive.
Give your name when you meet someone. Extend your hand. “Hi XX. Fanyu Zhao. How are you?” By stating my name.
4. Keep the conversation going!
Instead of sitting back and waiting for another kind soul to start a conversation, take the lead. Try to make your guest as comfortable as possible.
The approachable person is the one who makes eye contact with you and who is not actively engaged in a conversation or another activity such as reading a newspaper or working at a computer.
Not only are icebreakers a good way to start conversation, but some of the statements are accompanied by questions you can ask to keep the ball rolling. Don’t use a statement alone. Using a statement by itself is like lobbing the conversational ball blindfolded, not knowing where it will land or whether it will get tossed back.
- Tips for Starting with a Conversation
- What a beautiful day. What’s your favorite season of the year?
- I was truly touched by that movie. How did you like it? Why?
- This is a wonderful restaurant. What is your favorite restaurant? Why?
- What a great conference! Tell me about the sessions you attended.
- I was absent last week. What did I miss?
- That was an interesting program after lunch. What did you think?
- Presidential campaigns seem to start immediately after the inauguration. What do you think of the campaign process?
- I am so frustrated with getting this business off the ground. Do you have any ideas?
- • I am excited about our new mayor. How do you think her administration will be different from her predecessor’s?
- Your lawn always looks so green. What is your secret?
- We’ve been working together for months now. I’d like to get to know you better. Tell me about some of your outside interests.
- You worked pretty hard on that stair stepper. What other equipment do you use?
- You always wear such attractive clothes. What are your favorite stores?
- What a beautiful home. How do you manage to run a house with four children?
- I read in the newspaper that our governor has taken another trip overseas. What do you think of all his travel?
- Easy Openers: You will be successful if you just take the initiative and give it a try. You’ll be surprised by how easy it is and at the positive reinforcement you get from people when you start a conversation. Remember the following four steps and you are well on your way to an excellent chat.
- Make eye contact.
- Smile.
- Find that approachable person!
- Offer your name and use theirs.
- Break into a group of five conversation:
- Show interest in the speaker, but stand slightly away from the group. A group this size is slow to warm, so first let them become accustomed to seeing you. Slowly, they will shift to bring you into the circle.
- Ease into the group by demonstrating that you’ve been listening. Look for welcoming signs such as them asking your opinion or physically shifting positions to better include you.
- Initially, it is best to find a point of agreement; barring that, just acknowledge the speaker. Wait before rocking the boat with a big wave of radical opinions. Before offering your views, let the group warm to you. If you come on too strong too fast, the group will resent your intrusion and disband. Then you have to start all over again, looking to chat with someone you haven’t just offended!
5. Let’s Give ’Em Something to Talk About
Your mission is to get your conversation partners talking about themselves. Most people enjoy the opportunity to share their stories, and if you give them the chance, they’ll start talking. This is a no-brainer route to small talking success.
- Asking.
By asking open-ended questions, you offer your conversation partner the opportunity to disclose as much or as little as she wants. These questions demand more than a simple yes or no answer, yet they make no stressful demands.
-
Digging Deeper
After asking the greeting type question such as “How are you?”, follow up with deep question.
These everyday inquiries are just a few other ways of saying hello. It’s almost universally understood that these questions are a form of greeting, not a sincere inquiry.
Digging in deeper indicates you truly desire a response and are prepared to invest time in hearing the response.
Dig in deeper based on your observation.
6. Hearing Aids and Listening Devices
Scientific research has shown that people are capable of listening to approximately 300 words per minute. On the flip side, most of us can only speak at 150 to 200 words per minute.
The dilemma is that we have the capacity to take in much more information than one person can divulge at any given time.
Attentive listening has three parts: visual, verbal, and mental. Combine these elements, and powerful listening results.
- Listening is seen, not just heard
Listening is more than just hearing. In a normal two-person conversation, verbal components carry less than 35% of the social meaning of the situation, while nonverbal components account for over 65%. It’s critical to maintain eye contact when you are listening to another person.
Gestures show what the counterpart’s attitude.
-
Verbalise your listening
There are numerous verbal cues to let the speaker know you are fully engaged in the conversation. These brief comments tell the speaker that you are interested and want to know more. You can use verbal cues to show that you have a positive response, that you disagree, or that you want to hear more about something in particular.
| If you want to show that you are: | Say: |
|---|---|
| Interested in hearing more … | Tell me more. What was that like for you? |
| Taking it all in… | Hmmm, I see … |
| Responding positively… | How interesting! What an accomplishment! |
| Diverging… | On the other hand, what do you think … ? |
| Expanding on the idea… | Along that same line, do you … ? Why? |
| Arguing/refuting… | What proof do you have of that? |
| Involving yourself … | Could I do that? What would it mean to me? |
| Clarifying … | I’m not sure I’m clear on your feelings about… |
| Empathising… | That must have been tough/frustrating, et cetera. |
| Probing… | What do you mean by that? How were you able to manage? |
| Seeking specifics… | Can you give me an example? |
| Seeking generalities… | What’s the big picture here? |
| Looking to the future… | What do you think will happen next? |
| Reviewing the past… | What happened first? |
| Seeking likenesses / differences | Have you ever seen anything like this? What’s the opposing point of view? |
| Seeking extremes / contrasts | What’s the downside? / What’s the optimum? |
Other verbal listening cues function to redirect the conversation by transitioning to another topic. Examples of cues that offer a seamless segue include:
- That reminds me of…
- I’ve always wanted to ask you…
- I thought of you when I heard…
- Do you mind if I change the subject?
- There’s something I’ve wanted to ask of someone with your expertise.
All these verbal cues indicate that you are fully present. Just as important, these cues encourage others to continue speaking. Imagine someone asks you a question, and you respond with a one-sentence answer. You are uncertain as to how much information they are truly interested in learning. Added verbal cues as you respond assure you that their interest is sincere.
- Tips for Tip-Top Listening
- Learn to want to listen. You must have the desire, interest, concentration, and self-discipline.
- To be a good listener, give verbal and visual cues that you are listening.
- Anticipate excellence. We get good information more often when we expect it.
- Become a **“whole body” listener: Listen with your ears, your eyes, and your heart. **
- Take notes. They aid retention.
- Listen now, report later. Plan to tell someone what you heard, and you will remember it better.
- Build rapport by pacing the speaker. Approximate the speaker’s gestures, facial expressions, and voice patterns to create comfortable communication.
- Control internal and external distractions.
- Generously give the gift of listening.
- Be present, watch the tendency to daydream. Don’t drift off from conversations.
7. Prevent Pregnant Pauses with Preparation
- Do not let old acquaintances be forgotten
Seek out what’s new and keep the conversation rolling with questions. Like…
- Bring me up to date on . . .
- What’s been going on with work since I last saw
you? - What has changed in your life since we spoke last?
- How’s your year been?
But do not ask about other’s wife / jobs / children, if you do not know the person well
-
Preparing for the long haul
When there is nothing to talk about! Here are
some examples of interviewing questions you can customise to fit your own personality: (the book gives the following examples)- What do you enjoy most about this season of the year?
- What got you involved in this organisation/event?
- If you weren’t here, what would you be doing at this very moment?
- If you could meet any one person, whom would you choose?
- Tell me about an issue that matters a great deal to you.
- What has been your most important work experience?
- Limelight Etiquette
First, disclose information about yourself that is comfortable and uncontroversial. Lead with easy, positive, and light information. Building trust and intimacy over time creates friendships. Having a conversation is a little like peeling an onion—you want to proceed in layers, matching the level of intimacy shared by your partner.
You aren’t limited to talking about events and experiences. You can share feelings, opinions about books you’ve read, restaurants you’ve visited, and movies you’ve seen.
Speak no evil: Barring exceptional circumstances, avoid these often controversial topics that can stop a conversation in its tracks:
- Stories of questionable taste
- Gossip
- Personal misfortunes, particularly current ones
- How much things cost!
- Controversial subjects when you don’t know where people stand
- Health (yours or theirs). The exception is when you’re talking with a person who has an obvious new cast, crutches, or bandage. In that situation, the apparent temporary medical apparatus is free information. If you skirt the issue, it’s a bit like having an elephant in your living room and ignoring it.
When in doubt, leave it out. Avoid any area that is likely to offend your conversation partner
Conversation Clout
-
Can you spell your name for me? Most of us know how to spell our names, we do not need to be asked first if we know how!
Instead: Please spell your name for me.
-
If I can find out … A low expectation is established when you use the word if. Raise expectations. Instill confidence.
Instead: I will look into this and get back to you one way or the other.
-
I’m only the… Everyone’s role or job is important. This is demeaning to oneself. Define the capabilities and responsibilities in
your area of expertise.Instead: My responsibilities are focused on Website development. I will be glad to check with sales about your order.
-
I can’t meet with you this morning. This projects an unwillingness to deliver the best possible outcome. Or it projects a burden. In either
case say what you can do, not what you cannot.Instead: I can be there by three this afternoon.
-
I’ll try to get this back to you this week. The word try conveys the underlying message that this is not something that is dependable.
Instead: I’ll get to you no later than next week.
Tell people what you will do, not what you hope to do. -
You’ll have to call me tomorrow. This is a busy time for me. This sounds like a person giving orders and placing another burden on my already heavy load! And I don’t like to be bossed around.
Instead: *You can call me tomorrow. That’s a better time for me.
No say no, but say what you can.
9. Crimes and Misdemeanours
-
Don’t be interpreter.
Do not interpret. The interrupter is
characterised by high drive, determination to make her point, and a lack of patience.There are only three good reasons for interrupting. The first is that you need to exit immediately. The second is that the topic of conversation is too uncomfortable to bear, and you need to change the subject right away. And the third is if you are in the company of a monopoliser who has refused to offer you a natural break in the conversation for more than five minutes.
10. The Graceful Exit
There are ways to artfully exit a conversation that leave the other person’s ego intact. I find that many people remain in a conversation longer than they should for two reasons: they feel trapped, especially if it’s just a two-person dialogue, or they are so comfortable that they don’t want to leave.
- When you prepare to depart a conversation, recall why you originally connected with your conversation partner and bring the conversation back to that topic.
For example:
Tom, (1) it’s been wonderful talking with you about the changes impacting the health-care industry. (2) I need to catch up with another client before she leaves. (3) Thanks for sharing your expertise.
Notice that the author didn’t make excuses for my leaving. The author didn’t say I had to call the babysitter or that I needed to return a page. That well-known adage “honesty is the best policy”
You clearly state that the reason you are leaving the conversation is that you need to do something. There is no mistaking the fact that you have a specific agenda that you are trying to accomplish.
-
A Little Appreciation goes a long way
Ending a conversation by showing appreciation for the interchange provides an upbeat way to leave on a positive note. Thanking others for their time, expertise, or the sheer joy of the conversation is always welcome.
Remember to end the conversation the same way you began it—with a smile and a handshake. Even if you have to get up and walk around the table to do this, make sure you do. You make a lasting impression when you seal a conversation with a handshake.
-
Parting is such sweet sorrow
If you’ve met someone with whom you’d like to further a relationship, the best way to exit is to ask to see him again.
11. The conversational Ball is in your court!
A cheat sheet of tips here. Take the risk and assume the burden, and do start to talk.
Fifty Ways to Fuel a Conversation
- Be the first to say hello.
- Introduce yourself to others.
- Take risks and anticipate success.
- Remember your sense of humour.
- Practice different ways of starting a conversation.
- Make an extra effort to remember people’s names.
- Ask a person’s name if you’ve forgotten it.
- Show curiosity and sincere interest in finding out about others.
- Tell others about the important events in your life. Don’t wait for them to draw it out.
- Demonstrate that you are listening by restating their comments in another way.
- Communicate enthusiasm and excitement about your subjects and life in general.
- Go out of your way to try to meet new people wherever you are.
- Accept a person’s right to be an individual with different ideas and beliefs.
- Let the natural person in you come out when talking with others.
- Be able to succinctly tell others—in a few short sentences—what you do.
- Reintroduce yourself to someone who is likely to have forgotten your name.
- Be ready to tell others something interesting or challenging about what you do.
- Be aware of open and closed body language.
- Smile, make eye contact, offer a handshake, and go find the approachable person.
- Greet people that you see regularly.
- Seek common interests, goals, and experiences with the people you meet.
- Make an effort to help people if you can.
- Let others play the expert.
- Be open to answering common ritualistic questions.
- Be enthusiastic about other people’s interests.
- See that the time is balanced between giving and receiving information.
- Be able to speak about a variety of topics and subjects.
- Keep up to date on current events and issues that affect our lives.
- Be willing to express your feelings, opinions, and emotions to others.
- Use “I” when you speak about your own feelings and personal things, rather than “you.”
- Visually show others that you are enjoying your conversation with them.
- Be ready to issue invitations to others to join you for other events/activities to further the relationship.
- Find ways to keep in touch with friends and acquaintances you meet.
- Seek out others’ opinions.
- Look for the positive in those you meet.
- Start and end your conversations with the person’s name and a handshake or warm greeting.
- Take the time to be friendly with your neighbours and coworkers.
- Let others know that you would like to get to know them better.
- Ask others about things that they have told you in previous conversations.
- Listen carefully for free information.
- Be ready to ask open-ended questions to learn more.
- Change the topic of conversation when it has run its course.
- Always search for the things that really get another excited.
- Compliment others about what they are wearing, doing, or saying.
- Encourage others to talk to you by sending out positive signals.
- Make an effort to see and talk to people you enjoy.
- When you tell a story, present the main point first and then add the supporting details.
- Include everyone in the group in conversation whenever possible.
- Look for signs of boredom or lack of interest from your listener.
- Prepare ahead of time for each social or business function.
12. Make the most of networking events!
Do you dread receptions, banquets, and other business-related social events? Does attending another open house make you want to run inside your own and lock the door? You’re not alone. Many of us are apprehensive about these situations, because most of us either hate entering rooms where we don’t know anyone or hate spending time with people we don’t know well. Keeping a conversation going during such occasions is an ordeal.
But for business professionals, these occasions represent opportunities to develop business friendships and broaden our networks. Whether you realise it or not, networking happens all the time.
Everyone learns the technical skills required for their jobs, but not everyone places importance on conversational skills. The ability to talk easily with anyone is a learned skill, not a personality trait. Acquiring it will help you develop rapport with people and leave a positive impression that lasts longer than an exchange of business cards.
- A few tips:
- Be the first to say hello!
- Introduce yourself. Act as if you’re the host and introduce new arrivals to your conversation partner or partners.
- Smile first and always shake hands when you meet someone.
- Take your time during introductions! Make an extra effort to remember names, and use them frequently in the conversation.
- Maintain eye contact in any conversation. Many people in a group of three or more look around in the hope that others will maintain eye contact on their behalf. Yet people don’t feel listened to if you’re not looking at them.
- Get somebody to talk about why they’re attending the event. You are now on your way to engaging them in conversation.
- Show an interest in every person. The more interest you show, the more wise and attractive you become to others.
- Listen carefully for information that can keep the conversation going.
- Remember, people want to be with people who make them feel special, not people who are “special.” Take responsibility to help people you talk to feel as if they’re the only person in the room.
- Play the conversation game. When someone asks How’s business? or What’s going on? answer with more than Not much. Tell more about yourself so that others can learn more about you.
- Be careful with business acquaintances. You wouldn’t want to open a conversation with: How’s your job at? What if that person just got fired or laid off? Be careful when you’re asking about an acquaintance’s spouse or special friend; you could regret it.
- Don’t act like you’re an FBI agent. Questions like What do you do?, Are you married?, Do you have children?, and Where are you from? lead to dead-end conversations.
- Be aware of body language. Nervous or illatease people make others uncomfortable. Act confident and comfortable, even when you’re not.
- Be prepared. Spend a few minutes before an anticipated event preparing to talk easily about three topics. They will come in handy when you find yourself in the middle of an awkward moment . . . or while seated at a table of eight where everyone is playing with their food.
- Show an interest in your conversation partner’s opinion, too. You’re not the only person who has opinions about funding the space program or what will happen to the stock market.
- Stop conversation monopolists in their tracks. If possible, wait for the person to take a breath or to pause, then break in with a comment about their topic. Immediately redirect the conversation in the direction you wish it to go.
- Be prepared with exit lines. You need to move around and meet others.
- Don’t melt from conversations. Make a positive impression by shaking hands and saying good-bye as you leave.
13. Surviving the singles scene
- Don’t think of what you’re doing as “singles” socialising. Just think of it as networking.
You have something to offer others, and they have something to offer you: connection to humanity.
-
You don’t have to make small talk immediately upon entering.
Stand in the doorway and survey the scene. This accomplishes two things: You get a moment to stabilize yourself and get your bearings, and you are framing yourself for everyone to see; they will perceive you as a selfconfident person and unconsciously hope for the chance to speak with you. Self-confidence is probably the single most powerful magnet, right after good looks.
-
Follow up the conversation.
With creative usage of these three elements (questions, follow-up comments, follow-up questions), the possibilities and variations in conversation are virtually limitless. As long as you stay focused on the conversation, you can keep it going.
15. Feel-Good Factor
Here’s how to build rapport that leads to success in every business relationship.
- Use small talk as a picture frame around business conversations. Begin and end with small talk when making a presentation to a client, selling a widget, negotiating a contract, providing a service, or conferencing with your child’s teacher. A study conducted with physicians showed those who spend a few minutes asking patients about their family, their work, or summer plans before and/or after an examination are less likely to be sued than those who don’t.
People don’t sue people they care about. And we care about people who show they care about us.
-
Express empathy. Everyone is entitled to be listened to, even when in the wrong. Consider the client who sees the stock market rise 30 percent but not his own portfolio. The stockbroker knows the client insisted on picking the stocks himself, but it would be a mistake to make the client “wrong.” It’s better to say, I realize it’s frustrating to experience this. What can we do from here? That goes a long way to defusing negative emotions and helping the client feel better about this relationship—rather than tempted to move on to another stockbroker.
-
Greet people warmly, make eye contact, and smile. Be the first to say hello. Be careful, you might be viewed as a snob if you are not the first to say hello. People often go back to their favourite restaurants because the host greets them with a sincere smile, looks at them directly, and welcomes them with warmth.
-
Use the person’s name in conversation. You are more likely to get special treatment by using the person’s name. If you don’t know someone’s name, take a moment to ask, and then repeat it. Be sure to pronounce it correctly. And never presume your conversation partner has a nickname. My name is Debra, not Debbie. I don’t feel good when people call me Debbie. It’s a little thing that has big importance.
-
Show an interest in others. In response to our high-tech environment of e-mail and fax broadcasts, we need “high touch” more than ever. That’s what you create when you show an interest in the lives of your customers/clients/patients every chance you get.
-
Dig deeper. When you engage in a conversation, don’t leave it too quickly. If your customer / client / patient mentions her vacation, pick up on the cue and dig deeper. Ask where she went, what she did, what the highlight was, if she would go back. You’ll make her feel good about her life and about taking time with you.
Always follow up a question like How’s work? with What’s been going on at work since the last time we spoke? This way he or she knows you really want to hear about what is going on with work.
-
Be a good listener. That means making eye contact and responding with verbal cues to show you hear what the speaker says.
Verbal cues include the phrases: Tell me more, What happened first?, What happened next?, That must have been difficult, and so on. Using them makes people feel actively listened to.
-
Stop being an adviser. When you mention a problem you might be having with an employee or an associate, do people offer advice without asking any questions? Have you ever put together a résumé and, as soon as you sent it out, someone told you it was too long or too short or too detailed or not detailed enough? Jumping in with unsolicited advice happens annoyingly often. Instead of advice, give understanding with simple phrases like I know you can work out a solution or I hope the job hunt goes well for you. Offer advice only when you are specifically asked for it.
People say something does not mean they are asking for an advice. Probably, people are just want to speak, and want you to listen. So, do not give advice if people is not asking for.