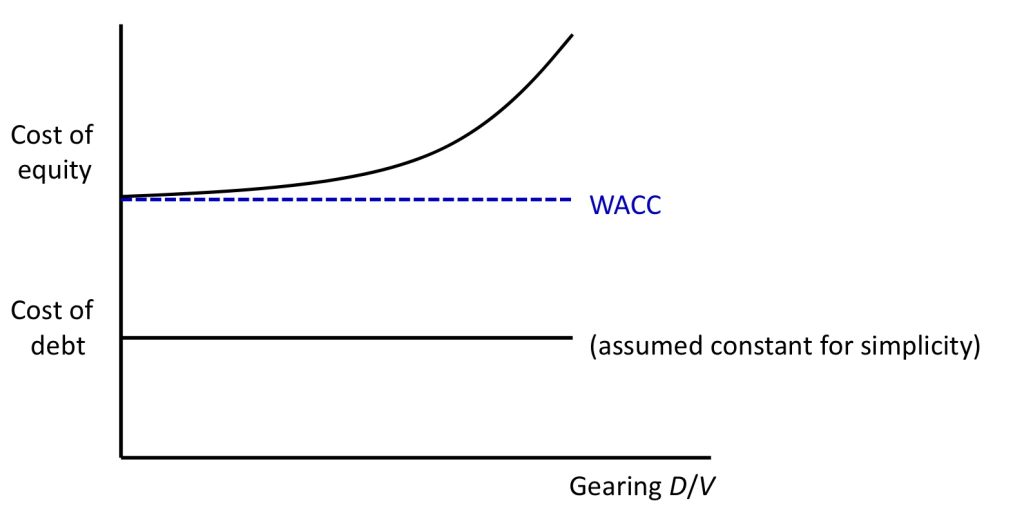
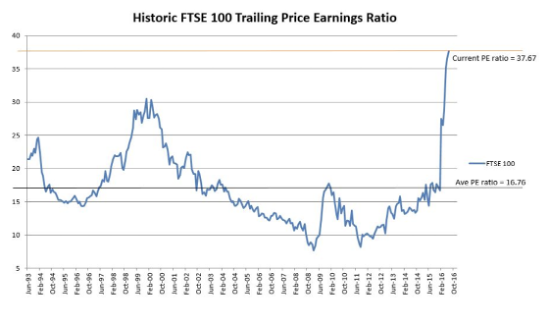
The authors noted the financial crisis of 2008 was caused by mainly three reasons.
- U.S. financial sectors misallocated resources to real estate.
- Commercial and Investment banks had a large proportion of their instruments in their Balance Sheet.
- Investments were largely financed with short-term debts.
The following will illustrate why those facts happen.
1. Misallocation of Investment
Step 1. World Crisis pushed up risks.
The financial crisis in emerging markets, East Asia Econ Collapsed, `Russia Defaulted, South America, etc made investors circumspect.
Step 2. Capital Controls made CA surplus.
To react to those unexpected events and prevent domestic industries from the incumbents, governments started to conduct capital controls. Also, investors were unwilling to invest (they cut down investments and even consumptions) or charge a high-level risk premium. A number of countries became net exporters.
Step 3. “dot-com” bubble derived another global crisis.
Those exporters then had a current accounts surplus and transferred the CA surplus into “savings” (investment). Those savings were invested into the high-return business, the IT industry. However, another nightmare happened that is the “dot-com” bubble collapsed around the 2000s.
Step 4. CB QE and US financial innovations made a housing bubble
Central Banks QE, lowered the interest rate, which ignited demand for housing. The house price spiked. In the U.S., financial innovation (securitization) drew more marginal-credit-quality buyers into the market. The crisis manifested itself.
Step 5. Asymmetric information enforced the bubble.
Because rating agencies were at a distance from the homeowner, they could process only hard information. Asymmetric information enforced the bubble. Housing prices surged to prevent “default”.
Step 6. Securitization Iterate itself.
The slicing and dicing through repeated securitization of the original package of mortgages created very complicated securities. The problems in valuing these securities were not obvious when house prices were rising and defaults were few.
But as the house prices stopped rising and defaults started increasing, the valuation of these securities became very complicated.
2. Why Did Bank hold those instruments?
The key answer is bankers thought those securities were worthwhile investments, despite their risks. Risks were vague and unable to be evaluated.
it is very hard, especially in the case of new products, to tell whether a financial manager is generating true excess returns adjusting for risk, or whether the current returns are simply compensation for a risk that has not yet shown itself but that will eventually materialize.
Several facts manifested the problem.
- 1. Incentive at the Top
CEOs’ performance is evaluated based in part on the earnings they generate relative to their peers. Peer Pressure, which came from holding financial instruments to increase returns, mutually increased the willingness to hold those financial instruments.
- 2. Flawed Internal Compensation and Control
The top management wants to maximise the long-term bank value and goals. However, many compensation schemes are paid for short-term risk-adjusted performance. The divergency gave managers an incentive to take risks in the short term.
It is not said that the Risk management team is unaware of such incentives. However, they may be unable to fully control them, because tail risks, by the nature, are hard to quantify before they occur.
- 3. Short-term Debt
Given the complexity of bank risk-taking, and the potential breakdown in internal control processes, investors would have demanded a very high premium for financing the bank long term. By contrast, they would have been far more willing to hold short-term claims on the bank, since that would give them the option to exit — or get a higher premium — if the bank appeared to be getting into trouble.
In good times, short-term debt seems relatively cheap compared to long-term capital and the costs of illiquidity remote. Markets seem to favor a bank capital structure that is heavy on short-term leverage. In bad times, though, the costs of illiquidity seem to be more salient, while risk-averse (and burnt) bankers are unlikely to take on excessive risk. The markets then encourage a capital structure that is heavy on capital.
- 4. The Crisis Unfolds
Housing Price decreased, => MBS fall in value and becaome hard to price. Balance sheet destorted, and debt level held, and equity shrinked.
Every parties sold out, drived price down again and again.
Panic (no confidence) spreaded worldwide.
Interbank lendings were forzen as inadequate credits.
- 5. The `Credit Crunch
Banks were reluctant to lend due to two reasons. One possibility is that they worry about borrower credit risks. A second is that they may worry about having enough liquidity of their own, if their creditor demands funds.
- Dealing with the Crunch
Banks still fear threats from illiquidity. Illiquid assets still compose significant portions of banks and non-banl balance sheets. The price of those illiquid assets fluctuated largely, because liquidty asset could be easily exchanged or sold out for cash, but illiquid assets were unable to do so so that price shrinked and damaged the balance sheet. Debts held constant, but assets shrinked, resulting in shrinkage of equity, and increase in leverage and financial burden.
Coins have two sides. Low prices mean not only insolvent, but also tremendous buying opportunity. The pandic manified the expectation of insolvency, plus illiquid market condition made the fact that less money was availab to buy at the price. Selling iterated itself.
CB standed out, provided liquidty to financial institutes.
However, an interesting thing happened. CB’s intervention to lend against all manner of collateral may not be a unmitigated bless, because it may allow weak entities to continue holding illiquid assets.
Possible ways to reduce the overhand
1. Authorities offer to buy illiquid assets through auctions. `This can reverse a freeze in the market caused by distressed entities. Fair value from the aution can be higher than the prevailing market price. 2. government ensures the stability of financial system that holds illiquid assets through the recapitalization of entities that have a realistic possibility of survival. (我国,纳入国有).
Reference
Diamond, Douglas W. and Rajan, Raghuram G., The Credit Crisis: Conjectures About Causes and Remedies (February 2009). NBER Working Paper No. w14739, Available at SSRN: https://ssrn.com/abstract=1347262