Fanyu Zhao

Here is a review of the method of Lagrangian method. We find that maximising a utility function s.t. a budget constant by using Lagrangian could also get the MRS.

$$\max_{x,y} U(x,y)\quad s.t.\quad BC$$

Or, in a Cobb-Douglas utility.

$$\max_{x,y} x^a y^b\quad s.t.\quad p_x x+p_y y\leq w $$

Using the Lagrange Multiplier,

$$\mathcal{L}=x^a y^b +\lambda (w-p_x x- p_y y)$$

Discuss the complementary slackness, and take F.O.C.

$$ \frac{\partial \mathcal{L}}{\partial x}=0 \Rightarrow a x^{a-1}y^b=\lambda p_x $$

$$ \frac{\partial \mathcal{L}}{\partial y}=0 \Rightarrow x^a b y^{b-1}=\lambda p_y $$

Divide those two equations then we get,

$$ \frac{MU_x}{MU_y}=\frac{ay}{bx}=\frac{p_x}{p_y}=MRS_{x,y} $$

After knowing the Marshallian Demandm \(x=f(p_x,p_y,w)\), we can then calculate the elasticity.

• \(\varepsilon=\frac{\partial x}{\partial p_x}\frac{p_x}{x}\), elasticity to price of x.
• \(\varepsilon_I=\frac{\partial x}{\partial w}\frac{w}{x}\), elasticity to wealth.
• \( \varepsilon_{xy}=\frac{\partial x}{\partial p_y}\frac{p_y}{x} \), elasticity to price of y.

Meaning of Lambda

Review the graphic version of the utility maximisation problem, the budget constraint is the black plane, the utility function is green, and the value of utility is the contour of the utility function.

After solving the utility maximisation problem, we would get \(x^*\) and \(y^*\) (they have exact values). Then, plug them back into the F.O.C., we get easily get the numerical value of \(\lambda\).

As \(\frac{\partial \mathcal{L}}{\partial w}=\lambda\), \(\lambda\) represents how does the utility changes if wealth changes a unit.

\(\lambda\) is like the slope of the utility surface. With the increase, the wealth, the budget constraint (the black wall) moves outwards, and then the changes would result in an increase of the utility value, which is the intersection of the utility surface and the budget constraint surface.

Similarly, the utility function could be replaced with production and has a similar implication of output production.

Geographical Meaning

\(\lambda\) is when the gradient of the contour of the utility function is in the same direction as the gradient of constraint. Or says, the gradient of \(f\) is equal to the gradient of \(g\).

In another word, the Lagrange multiplier \(\lambda\) gives the max and min value of \(x\) and \(y\), and also the corresponding changing speed of those max or mini values of our objective function, \(f\), if the constraint, \(g\), releases.

Lagrange Multiplier:

Simultaneously solve \(\nabla f=\lambda\nabla g\), and \(g=0\). \(f\) here is the objective function (utility function in our case), and \(g\) here is the constraint (the budget constraint in our case).

Reference

Thanks to the video from Professor Burkey, that helps a lot to let me rethink the meaning of lambda.

https://www.youtube.com/watch?v=O3MFXT7AdPg

And the geographic implication of Lagrange multiplier method.

https://www.youtube.com/watch?v=8mjcnxGMwFo

Derivations

We here derive why \(MRS_{x,y}=\frac{MU_x}{MU_y}\).

Let \(U(x,y)=f(x,y)\), and we know, by definition, MRS measures how many units of x is needed to trade y holding utility constant. Thus, we keep the utility function unchanged, \(U(x,y)=C\), and take differentiation and find \(-dy/dx\).

$$f(x,y) dx=C dx$$

$$ \frac{\partial f(x,y)}{x}+\frac{\partial f(x,y)}{\partial y}\frac{\partial y}{\partial x}=0 $$

$$\frac{\partial y}{\partial x}=-\frac{\frac{\partial f(x,y)}{\partial x}}{\frac{\partial f(x,y)}{\partial y}}=\frac{MU_x}{MU_y}$$

Therefore,

MRS_{x,y}=-\frac{dy}{dx}=\frac{MU_x}{MU_y}

$$|MRS_{x,y}|=-\frac{dy}{dx}=\frac{MU_x}{MU_y} $$

Example 1

$$U=x^2+y^2$$

$$MRS_{x,y}=\frac{MU_x}{MU_y} =\frac{x}{y}$$

Example 2

$$U=x\cdot y$$

, which is similar as the Cobb-Douglas form but has exponenets zero.

$$MRS_{x,y}=\frac{MU_x}{MU_y} =\frac{y}{x}$$

Example 3

MRTS

Marginal Rate of Technical Substitution (MRTS) measures the amount of cost which a specific input can be replaced for another resource of production while maintaining a constant output.

$$MRTS_{K,L}=-\frac{\Delta K}{\Delta L}=-\frac{d K}{d L}=\frac{MP_L}{MP_K}$$

How to derive that?

Recall the Isoquant that is equivalent to the contour line of the output function. MRTS is like the slope of the isoquant line. We let,

$$Q=L^a K^b$$

Then,

$$MP_K=\frac{\partial Q}{\partial K}=b L^A K^{b-1}$$

$$MP_L=\frac{\partial Q}{\partial L}=a L^{a-1}K^b$$

$$MRTS=\frac{ b L^A K^{b-1} }{ a L^{a-1}K^b }=\frac{aK}{bL}$$

In short, MRTS is a similar concept to MRS, but in the output aspect.

Cobb-Douglas Utility function

$$U=C x^a y^b$$

While applying the Cobb-Douglas formed utility function, we are actually proxy the preference of people. (The utility function is like a math representation if individuals’ preference is rational). In the utility function, we are focusing more on the Marginal Rate of Substitution between goods.

$$MRS_{x,y}=\frac{MU_x}{MU_y}=\frac{\partial U/\partial x}{\partial U/\partial y}=\frac{Cax^{a-1}y^b}{Cx^a by^{b-1}}$$

$$MRS_{x,y}=\frac{ay}{bx}$$

P.S. Cobb-Douglas gives the same MRS to CES utility function. While solving the utility maximisation problem, we take partial derivatives to the lagrangian and then solve them. Those steps are similar to calculating the MRS.

The key is that the number or value of the utility function does not matter, but the preference represented by the utility function is more important. Any positive monotonic transformation will not change the preference, such as logarithm, square root, and multiply any positive number.

Exponents Do Not Matter

The powers of the Cobb-Douglas function does not really matter as long as they are in the “correct” ratio. For example,

$$ U_1=Cx^7y^1,\quad and \quad U_2=Cx^{7/8}y^{1/8} $$

$$MRS_1=\frac{7y}{x}\quad and \quad MRS_2=\frac{7y/8}{x/8}=\frac{7y}{x}$$

Therefore, we can find that those two utility functions represent the same preference!

Or we can write \(U_1=(U_2)^8 \cdot C^{-7}\). Both taking exponent and multiplying a positive constant are positive monotonic transformations. Therefore, the powers of Cobb-Douglas do not really matter to represent the preference. (\(U=Cx^a y^{1-a}\) the exponents of the utility function does not have to be sum to one).

$$U=x^a y^b \Leftrightarrow x^{\frac{a}{a+b}}y^{\frac{b}{a+b}}$$

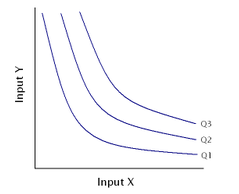
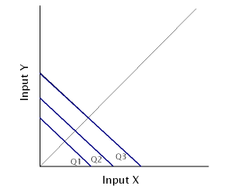
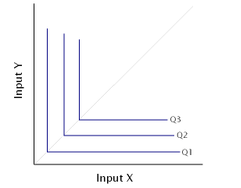
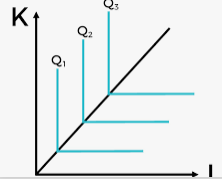
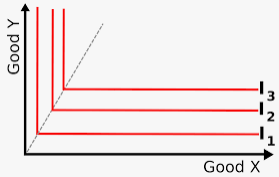
CES could be either production or utility function. It provides a clear picture of how producers or consumers choose between different choices (elasticity of substitution).

CES Production

The two factor (capital, labour) CES production function was introduced by Solow and later made popular by Arrow.

$$Q=A\cdot(\alpha K^{-\rho}+(1-\alpha)L^{-\rho})^{-\frac{1}{\rho}}$$

• \(\alpha\) measures the relative proportion spent across K and L.
• \(\rho=\frac{\sigma-1}{\sigma}\) is the substitution parameter.
• \(\sigma=\frac{1}{1-\rho}\) is the elasticity of substitution.

While identical producers maximise their profits and markets get competitive, Marginal Product of Labour and Marginal Product of Capital follow,

$$MP_L=\frac{\partial Q}{\partial L}=w$$

$$MP_K=\frac{\partial Q}{\partial K}=r$$

So we get,

$$ \frac{w}{r}=\frac{1-\alpha}{\alpha}(\frac{K}{L})^{\rho+1} $$

$$\frac{K}{L}=(\frac{\alpha}{1-\alpha}\frac{w}{r})^{\frac{1}{1+\rho}}$$

Here, we get the substitution of K and L is a function of the price, w & r. As we are studying the elasticity of substitution, in other words how W/L is affected by w/r, we take derivatives later. We denote \(V=K/L\), and \(Z=w/r\). Then,

$$V=(\frac{\alpha}{1-\alpha}Z)^{\frac{1}{1+\rho}}$$

The Elasticity of Substitution (the percentage change of K/L in terms of the percentage change of w/r) is,

$$ \sigma=\frac{dV/V}{dZ/Z}=\frac{dV}{dZ}\frac{Z}{V}=\frac{1}{1+\rho} $$

Therefore, we get the elasticity of substitution becomes constant, depending on \(\rho\). The interesting thing happens here.

• If \(-1<\rho<0\), then \(\sigma>1\).
• If \(0<\rho<\infty\), then \(\sigma<1\).
• If \(\rho=0\), then, \(\sigma=1\).

Utility Function

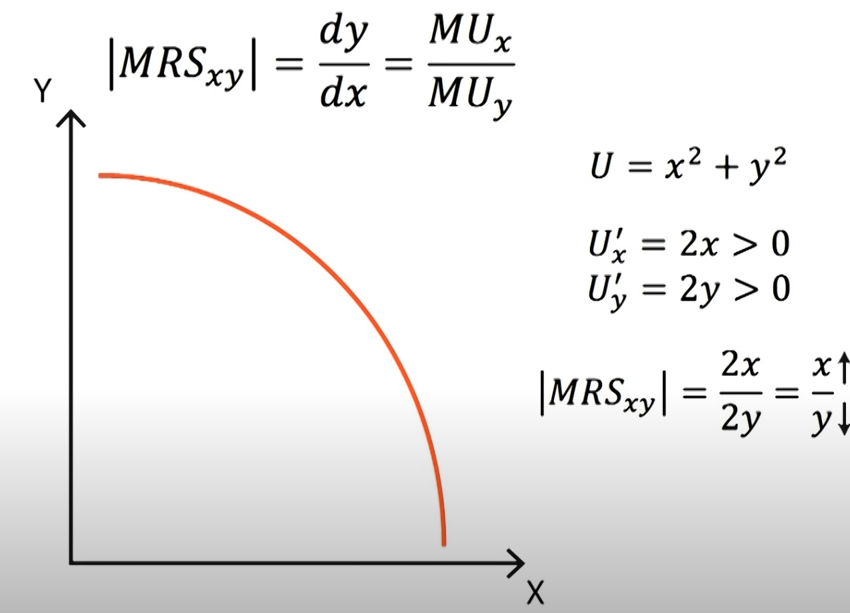
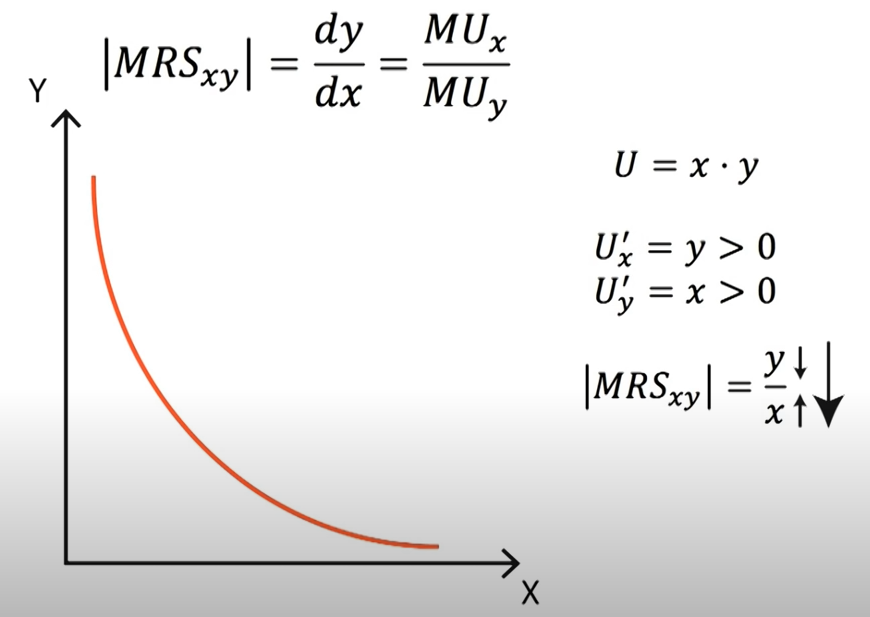
Marginal Rate of Substitution (MRS) measures the substitution rate between two goods while holding the utility constant. The elasticity between X and Y could be defined as the following,

$$ Elasticity=\frac{\%\Delta Y}{\% \Delta X}=\frac{\Delta Y/Y}{\Delta X/X}=\frac{X/Y}{\Delta X/\Delta Y} $$

The elasticity of substitution here is defined as how easy is to substitute between inputs, x or y. In another word, the change in the ratio of the use of two goods w.r.t. the ratio of their marginal price. In the utility function case, we can apply the formula,

$$\sigma=\frac{\Delta ln(X/Y)}{\Delta ln(MRS_{X,Y})}=\frac{\Delta ln(X/Y)}{\Delta ln(U_x/U_y)}= \frac{\Delta ln(X/Y)}{\Delta ln(U_x/U_y)} $$

$$\sigma=\frac{\frac{\Delta(X/Y)}{X/Y}}{\frac{\Delta (p_x/p_y)}{p_x/p_y}}$$

• \(U_x=\frac{\partial U}{\partial X}=p_x\)
• \(MRS_{X,Y}=\frac{dy}{dx}=\frac{U_x}{U_y}=p_x/p_y\) marginal price in equilibrium.

In the

$$ u(x,y)=(a x^{\rho}+b y^{\rho})^{1/\rho} $$

$$\sigma=\frac{1}{1-\rho}$$

If \(\rho=1\), then \(\sigma\rightarrow \infty\).

If \(\rho\rightarrow -\infty\), then \(\rho=0\).

Two common choices of CES production function are (1) Walras-Leontief-Harrod-Domar function; and (2) Cobb-Douglas function (P.S. but CES is not perfect, coz sigma always equal one).

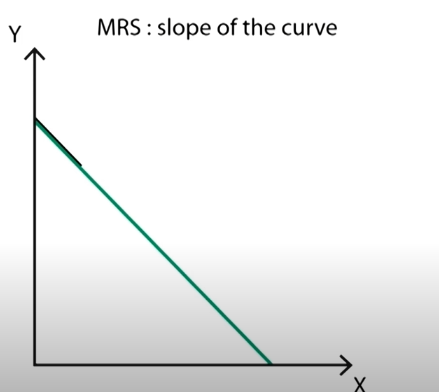
As \(\rho=1\), the utility function would be a perfect substitute.

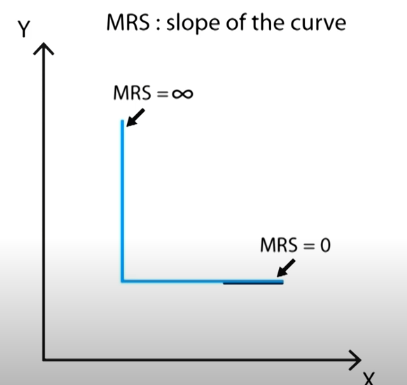
As \(\rho=-1\), the utility function would be pretty similar to the Cobb-Douglas form.

Later, the CES utility function could be applied to calculate the Marshallian demand function and Indirect utility function, and so on. Also, easy to show that the indirect utility function \(U(p_x,p_y,w)\) is homogenous degree of 0.

Reference

Arrow, K.J., Chenery, H.B., Minhas, B.S. and Solow, R.M., 1961. Capital-labor substitution and economic efficiency. The review of Economics and Statistics, 43(3), pp.225-250.