In Dutch Disease, certain sectors have enormous exports demand, which would drive the demand of currency for that country. Its currency appreciates. However, the rest sectors that may not have such huge amount of exports demand would also have to undergo an appreciation of currency. Export demands for goods and services in the rest sectors would decrease even severe.
Category: Learning
The Impact of Balance of Payments Flows
As noted earlier, the parity conditions may be appropriate for assessing fair value for currencies over long horizons, but they are of little use as a real-time gauge of value. There have been many attempts to find a better framework for determining a currency’s short-run or long-run equilibrium value. Let’s now examine the influence of trade and capital flows.
A country’s balance of payments consists of its (1) current account as well as its (2) capital and (3) financial account. The official balance of payments accounts make a distinction between the “capital account” and the “financial account” based on the nature of the assets involved. For simplicity, we will use the term “capital account” here to reflect all investment/financing flows. Loosely speaking, the current account reflects flows in the real economy, which refers to that part of the economy engaged in the actual production of goods and services (as opposed to the financial sector). The capital account reflects financial flows. Decisions about trade flows (the current account) and investment/financing flows (the capital account) are typically made by different entities with different perspectives and motivations. Their decisions are brought into alignment by changes in market prices and/or quantities. One of the key prices—perhaps the key price—in this process is the exchange rate.
Countries that import more than they export will have a negative current account balance and are said to have current account deficits. Those with more exports than imports will have a current account surplus. A country’s current account balance must be matched by an equal and opposite balance in the capital account. Thus, countries with current account deficits must attract funds from abroad in order to pay for the imports (i.e., they must have a capital account surplus).
When discussing the effect of the balance of payments components on a country’s exchange rate, one must distinguish between short-term and intermediate-term influences on the one hand and longer-term influences on the other. Over the long term, countries that run persistent current account deficits (net borrowers) often see their currencies depreciate because they finance their acquisition of imports through the continued use of debt. Similarly, countries that run persistent current account surpluses (net lenders) often see their currencies appreciate over time.
However, investment/financing decisions are usually the dominant factor in determining exchange rate movements, at least in the short to intermediate term. There are four main reasons for this:
- Prices of real goods and services tend to adjust much more slowly than exchange rates and other asset prices.
- Production of real goods and services takes time, and demand decisions are subject to substantial inertia. In contrast, liquid financial markets allow virtually instantaneous redirection of financial flows.
- Current spending/production decisions reflect only purchases/sales of current production, while investment/financing decisions reflect not only the financing of current expenditures but also the reallocation of existing portfolios.
- Expected exchange rate movements can induce very large short-term capital flows. This tends to make the actualexchange rate very sensitive to the currency views held by owners/managers of liquid assets.
Current Account Imbalances and the Determination of Exchange Rates
Current account trends influence the path of exchange rates over time through several mechanisms:
- The flow supply/demand channel
- The portfolio balance channel
- The debt sustainability channel
Let’s briefly discuss each of these mechanisms next.
The Flow Supply/Demand Channel
The flow supply/demand channel is based on a fairly simple model that focuses on the fact that purchases and sales of internationally traded goods and services require the exchange of domestic and foreign currencies in order to arrange payment for those goods and services. For example, if a country sold more goods and services than it purchased (i.e., the country was running a current account surplus), then the demand for its currency should rise, and vice versa. Such shifts in currency demand should exert upward pressure on the value of the surplus nation’s currency and downward pressure on the value of the deficit nation’s currency.
Hence, countries with persistent current account surpluses should see their currencies appreciate over time, and countries with persistent current account deficits should see their currencies depreciate over time. A logical question, then, would be whether such trends can go on indefinitely. At some point, domestic currency strength should contribute to deterioration in the trade competitiveness of the surplus nation, while domestic currency weakness should contribute to an improvement in the trade competitiveness of the deficit nation. Thus, the exchange rate responses to these surpluses and deficits should eventually help eliminate—in the medium to long run—the source of the initial imbalances.
The amount by which exchange rates must adjust to restore current accounts to balanced positions depends on a number of factors:
- The initial gap between imports and exports
- The response of import and export prices to changes in the exchange rate
- The response of import and export demand to changes in import and export prices
If a country imports significantly more than it exports, export growth would need to far outstrip import growth in percentage terms in order to narrow the current account deficit. A large initial deficit may require a substantial depreciation of the currency to bring about a meaningful correction of the trade imbalance.
A depreciation of a deficit country’s currency should result in an increase in import prices in domestic currency terms and a decrease in export prices in foreign currency terms. However, empirical studies often find limited pass-through effects of exchange rate changes on traded goods prices. For example, many studies have found that for every 1% decline in a currency’s value, import prices rise by only 0.5%—and in some cases by even less—because foreign producers tend to lower their profit margins in an effort to preserve market share. In light of the limited pass-through of exchange rate changes into traded goods prices, the exchange rate adjustment required to narrow a trade imbalance may be far larger than would otherwise be the case.
Many studies have found that the response of import and export demand to changes in traded goods prices is often quite sluggish, and as a result, relatively long lags, lasting several years, can occur between (1) the onset of exchange rate changes, (2) the ultimate adjustment in traded goods prices, and (3) the eventual impact of those price changes on import demand, export demand, and the underlying current account imbalance.
The Portfolio Balance Channel
The second mechanism through which current account trends influence exchange rates is the so-called portfolio balance channel. Current account imbalances shift financial wealth from deficit nations to surplus nations. Countries with trade deficits will finance their trade with increased borrowing. This behaviour may lead to shifts in global asset preferences, which in turn could influence the path of exchange rates. For example, nations running large current account surpluses versus the United States might find that their holdings of US dollar–denominated assets exceed the amount they desire to hold in a portfolio context. Actions they might take to reduce their dollar holdings to desired levels could then have a profound negative impact on the dollar’s value.
“Shifts in Global Asset Preferences” means would alter the components of assets allocation in the portfolio.
The Debt Sustainability Channel
The third mechanism through which current account imbalances can affect exchange rates is the so-called debt sustainability channel. According to this mechanism, there should be some upper limit on the ability of countries to run persistently large current account deficits. If a country runs a large and persistent current account deficit over time, eventually it will experience an untenable rise in debt owed to foreign investors. If such investors believe that the deficit country’s external debt is rising to unsustainable levels, they are likely to reason that a major depreciation of the deficit country’s currency will be required at some point to ensure that the current account deficit narrows significantly and that the external debt stabilises at a level deemed sustainable.
The existence of persistent current account imbalances will tend to alter the market’s notion of what exchange rate level represents the true, long-run equilibrium value. For deficit nations, ever-rising net external debt levels as a percentage of GDP should give rise to steady (but not necessarily smooth) downward revisions in market expectations of the currency’s long-run equilibrium value. For surplus countries, ever-rising net external asset levels as a percentage of GDP should give rise to steady upward revisions of the currency’s long-run equilibrium value. Hence, one would expect currency values to move broadly in line with trends in debt and/or asset accumulation.
Reference
CFA Readings
Value at Risk & Expected Shortfalls
Value at Risk – VaR
VaR is a probability statement about the potential change in the value of a portfolio.
Notation
$$Porb(x\leq VaR(X))= 1-c$$
$$ Prob\bigg(z \leq \frac{VaR(X)-\mu}{\sigma}\bigg)=1-c $$
- $c$ – confidence interval, i.e. $c=99\%$. Then $1-c = 1\% $
- $\mu$ and $\sigma$ are for $X$.
- For Example, if X is yearly return, then \mu_{252days}=252\cdot\mu_{1day}, and \sigma_{252days}=\sqrt{252}\cdot\sigma_{1day}
- $x$ here is the return. So, $c$ is the confidence interval, i.e. 99%.
- VaR focus on the tail risks. If x stands for return, then tail risk is on the left tail, z_{1-c}.
- If x is the loss, the tail risk is on the right tail. z_c
$$VaR(X) = \mu + \sigma\cdot \Phi^{-1}(1-c)$$
$$VaR(X) = \mu + \sigma\cdot z_{1-c}$$
- I.E.
If c=99\%, then 1-c=1\%, so z_{1-c}=z_{0.01} \approx -2.33
VaR(X) = \mu – 2.33\cdot \sigma
P.S.
The unit of VaR is the amount of loss, so it should be monetary amount. For example, if the total amount of portfolio is USD 1 million, then VaR = \$1m \cdot (\mu – 2.33\cdot \sigma).
Loss Distribution
Remember X is a distribution of loss. If we know the distribution of Portfolio Return R, R\sim N(\mu, \sigma^2), then what is the dist for X?
$$X \sim N(-\mu, \sigma^2)$$
Right! Loss is just the negative return. Also, the volatility would not be affected by plus / minus.
Expected Shortfall (ES)
Expected Shortfall states the Expected Loss during time T conditional on the loss being greater than the c^{th} percentile of the loss distribution.
Notation
$$ ES_c (X) = \mathbb{E}\bigg[ X|X\leq VAR_c(X) \bigg] $$
- Be attention here, X is a r.v., and x stands for return here! while the only variable in the ES_c(X) is c, the confidence level, instead of X.
- $c$ is the confidence level, i.e. $c$ = 99%.
- If x stands for return, then the VaR is the left-tail, z_{1-c}.
$$ ES_c (X) = \mathbb{E}\bigg[ X|X\geq VAR_c(X) \bigg] $$
- If x stands for loss (, which is the negative of return ), then the VaR is the right-tail, z_{c}.
Derivation
Notation Form
Consider, x is the return, then ES_c (X) = \mathbb{E}\bigg[ X|X\leq VAR_c(X) \bigg], and VaR_c(x)= \mu + z_{1-c}\sigma, where c is the confidence level c=99\% for example.
$$ES_c(X) = \frac{\int_{-\infty}^{VaR} xf(x)dx }{\int_{-\infty}^{VaR} f(x)dx } = \frac{\int_{-\infty}^{VaR} x \phi(x)dx }{\int_{-\infty}^{VaR} \phi(x)dx } =\frac{\int_{-\infty}^{VaR} x \phi(x)dx }{ \Phi(VaR) – \Phi(-\infty)} $$
$$= \frac{1}{ \Phi(VaR) – \Phi(-\infty) }\int_{-\infty}^{VaR}x \frac{1}{\sqrt{2\pi \sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}} dx $$
Replace z = \frac{x-\mu}{\sigma}, then x = \mu + z \sigma, and dx = \sigma dz
$$ = \frac{1}{\Phi(VaR)} \int_{-\infty}^{VaR}(\mu + z\sigma) \frac{1}{\sqrt{2\pi \sigma^2}} e^{-\frac{z^2}{2}}\sigma dz $$
$$ = \frac{1}{\Phi(VaR)}\mu \int_{-\infty}^{VaR}\frac{1}{\sqrt{2\pi }} e^{-\frac{z^2}{2}} dz + \sigma^2\int_{-\infty}^{VaR} z \frac{1}{\sqrt{2\pi \sigma^2}} e^{-\frac{z^2}{2}} dz $$
$$ = \frac{1}{\Phi(VaR)}\mu \Phi(VaR) – \frac{\sigma^2}{\Phi(VaR)}\int_{-\infty}^{VaR} \frac{1}{\sqrt{2\pi \sigma^2}} e^{-\frac{z^2}{2}} d(-\frac{z^2}{2}) $$
$$ = \mu – \frac{\sigma^2}{\Phi(VaR)} \frac{1}{\sqrt{2\pi \sigma^2}} \int_{-\infty}^{VaR} e^{-\frac{z^2}{2}} d(-\frac{z^2}{2}) $$
$$ = \mu – \frac{\sigma}{\Phi(VaR)} \frac{1}{\sqrt{2\pi }} e^{-\frac{z^2}{2}} |_{-\infty}^{VaR} $$
$$ = \mu – \frac{\sigma}{\Phi(VaR)} \frac{1}{\sqrt{2\pi }} e^{-\frac{VaR^2}{2}}= \mu – \frac{\sigma}{\Phi(VaR)} \phi(VaR)$$
Recall, VaR_c(x)= \mu + z_{1-c}\sigma, so \phi(VaR_c(x))= \phi(\mu + z_{1-c}\sigma) \leftrightarrow \phi(z_{1-c}) = \phi\bigg( \Phi^{-1}(1-c) \bigg), and \Phi(VaR_c(x))= \Phi(\mu + z_{1-c}\sigma) \leftrightarrow \phi(z_{1-c}) = \Phi\bigg( \Phi^{-1}(1-c) \bigg) = 1-c.
Thus,
$$ ES_c(X) =\mu – \frac{\sigma}{\Phi(VaR)} \phi(VaR)=\mu -\sigma \frac{\phi\big( \Phi^{-1}(1-c) \big)}{1-c}$$
VaR Form
we ‘sum up’ (integrate) the VaR from c to 1, conditional on 1-c.
$$ES_c(X) = \frac{1}{1-c} \int_c^1 VaR_u(X)du$$
$$ ES_c(X) = \frac{1}{1-c} \int_c^1 \bigg( \mu + \sigma\cdot \Phi^{-1}(1-u) \bigg) du $$
$$ =\mu + \frac{\sigma}{1-c} \int^1_c \Phi^{-1}(1-u) du $$
We let u = \Phi(Z), where Z \sim N(0,1). Then,
- $du =d(\Phi(z)) =\phi(z) dz$.
- $u\in (c,1)$, so $z = \Phi^{-1}(u)\in (z_c \ , \infty)$
Thus,
$$ ES_c(X) =\mu + \frac{\sigma}{1-c} \int^{\infty}_{z_c} \Phi^{-1}\big(1-\Phi(z)\big)\phi(z) dz $$
As 1-\Phi(z) = \Phi(-z)
$$ ES_c(X) =\mu + \frac{\sigma}{1-c} \int^{\infty}_{z_c} \Phi^{-1}(\Phi(-z))\phi(z) dz = \mu – \frac{\sigma}{1-c} \int^{\infty}_{z_c} z\phi(z) dz $$
$ \int_{z_c}^{\infty} z \phi(z)dz = \int_{z_c}^{\infty} z \frac{1}{\sqrt{2\pi}}e^{-\frac{z^2}{2}}dz = -\frac{1}{\sqrt{2\pi}} \int_{z_c}^{\infty} -e^{\frac{z^2}{2}}d(e^{-\frac{z^2}{2}})$
$=\frac{1}{\sqrt{2\pi}}e^{-\frac{z_c^2}{2}}=\phi(z_c)=\phi\big(\Phi^{-1}(c)\big)$, bring it back to $ES_c(X)$
$$ES_c(X) = \mu – \sigma\frac{ \phi\big(\Phi^{-1}(c)\big)}{1-c}$$
Morden Portfolio Theory
- $x$ – vector weights
- $R$ – vector of all assets’ returns
- $\mu = \mathbb{E}(R)$ – mean return of all assets
- $\Sigma = \mathbb{E}\bigg[ (R-\mu)(R-\mu)^T \bigg]$ – var-cov matrix of all assets
So,
- $\mu_x = x^T \mu$ – becomes a scalar now
- $\sigma^2 = x^T \Sigma x$ – collapse to be a scalar
Optimisation
- Maximise Expected Return s.t. volatility constraint.
$$ \max_{x} \mu_x \quad s.t. \quad \sigma_x \leq \sigma^* $$
- Minimise Volatility s.t. return constraint.
$$ \min_{x} \sigma_x \quad s.t. \quad \mu_x \geq \mu^* $$
Portfolio Risk Measures
By definition, the loss of a portfolio is the negative of return, L(x) = -R(x).
The Loss distribution becomes the same normal distribution with x-axis reversed.
- Volatility of Loss: \sigma(L(x)) = \sigma_x, the minus does not matter in the s.d.
- Standard Deviation-based risk measure: =\mathbb{E}(L(x)) + cz_{c}\sigma(L(x)), x-axis is revered, so z_{1-c} for return becomes z_c for loss.
- VaR: VaR_{\alpha}(x)=inf\bigg{ \mathscr{l}:Prob\big[ L(x)\leq \mathscr{l} \geq\big] \alpha \bigg}
- Expected Shortfall: ES_{\alpha}(x) = \frac{1}{1-\alpha} \int_{\alpha}^1 VaR_u(x) du. In other form, ES_{\alpha}(x)=\mathbb{E}\bigg( L(x)| L(x)\geq VaR_{\alpha}(x) \bigg)
As R \sim N(\mu, \Sigma),
- for our portfolio with weights x, mean = \mu, and \sigma_x = \sqrt{x^T \Sigma x}.
- for the loss, mean = -\mu, and \sigma_x = \sqrt{x^T \Sigma x}.
Taylor Series and Transition Density Functions
See my Github repo for full details.
https://github.com/eightsmile/cqf
1. Trinomial Random Walk
2. Transition Probability Density Function
The transition probability density function, p(y,t;y’,t’), is defined by,
$$ Prob(a<y'<b, at\ time \ t’ | y \ at \ time\ t) = \int_a^b p(yet;y’,t’)dy’$$
In words this is “the probability that the random variable y ′ lies between a and b at time t ′ in the future, given that it started out with value y at time t.”
Think of y and t as being current values with y ′ and t ′ being future values. The transition probability density function can be used to answer the question,
“What is the probability of the variable y ′ being in a specified range at time t ′ in the future given that it started out with value y at time t?”
Our Goal is to find the transition probability p.d.f., and so we find the relationship between p(y,t;y’,t’), and p(y,t;y’,t’-\delta t),
3. From the Trinomial model to the Transition Probability Density function
The variable y can either rise, fall or take the same value after a time step δt. These movements have certain probabilities associated with them.
We are going to assume that the probability of a rise and a fall are both the same, \alpha<\frac{1}{2} . (But, of course, this can be generalized. Why would we want to generalize this?)
3.1 The Forward Equation
Given {y,t}, or says {y,t} the current and previous. {y’,t’} are variate in the future time.
The probability of being at y’ at time t’ is related to the probabilities of being at the previous three values and moving in the right direction:
$$ p(y,t;y’,t’) = \alpha \ p(y,t;y’+\delta y,t’-\delta t) + \ (1-2\alpha) \ p(y,t;y’,t’-\delta t) + \alpha \ p(y,t;y’-\delta y,t’-\delta t) $$
Given {y,t}, we find relationship between {y’,t’} and {y’\pm \delta y,t’-\delta t} that is y’ and t’ a bit time previously.
Remember, our goal is to find a solution of p(.), we try to solve the above equation.
3.2 Taylor Series Expansion
We expand each term of the equation.
$$ p(y,t;y’,t’) = \alpha \ p(y,t;y’+\delta y,t’-\delta t) + \ (1-2\alpha) \ p(y,t;y’,t’-\delta t) + \alpha \ p(y,t;y’-\delta y,t’-\delta t) $$
Why we do that? Because there are too many variables in it, hard to solve it. We have to reduce the dimension.
$$ p(y,t;y’+\delta y,t’-\delta t)\approx \ p(y,t;y’,t) – \delta t \frac{\partial p}{\partial t’} +\delta y \frac{\partial p}{\partial y’} + \frac{1}{2}\delta y^2 \frac{\partial^2 p}{\partial y’^2} + O(\frac{\partial^2 p}{\partial t’^2}) $$
$$ p(y,t;y’,t’-\delta t)\approx \ p(y,t;y’,t) – \delta t \frac{\partial p}{\partial t’} + O(\frac{\partial^2 p}{\partial t’^2}) $$
$$ p(y,t;y’-\delta y,t’-\delta t)\approx \ p(y,t;y’,t) – \delta t \frac{\partial p}{\partial t’} -\delta y \frac{\partial p}{\partial y’} + \frac{1}{2}\delta y^2 \frac{\partial^2 p}{\partial y’^2} + O(\frac{\partial^2 p}{\partial t’^2}) $$
Plug them back into that equation, and after cancel out terms repeated we would left with,
$$ \frac{\partial p}{\partial t’} =\alpha \frac{\delta y^2}{\delta t} \frac{\partial^2 p}{\partial y’^2} + O(\frac{\partial^2 p}{\partial t’^2})$$
We drop those derivative terms with order greater and equal than O(\frac{\partial^2 p}{\partial t’^2}).
$$ \frac{\partial p}{\partial t’} =\alpha \frac{\delta y^2}{\delta t} \frac{\partial^2 p}{\partial y’^2} $$
In the RHS, we focus on \alpha \frac{\delta y^2}{\delta t}, firstly. The denominator and numerator have to be in the same order to make that term definite. Or, say \delta y \sim O(\sqrt{\delta t}).
We thus let c^2 = \alpha \frac{\delta y^2}{\delta t}
$$ \frac{\partial p}{\partial t’} =c^2 \frac{\partial^2 p}{\partial y’^2} $$
The above equation is also named Fokker–Planck or forward Kolmogorov equation.
Now, we have a partial differential equation. Solve it, we can get the form of p.
3.3 Backward Equation works similar.
$$ p(y,t;y’,t’) = \alpha \ p(y+\delta y,t+\delta t;y’,t’) + \ (1-2\alpha) \ p(y,t+\delta t;y’,t’) + \alpha \ p(y-\delta y,t+\delta t;y’,t’) $$
the dimension-reduced result is the blow, and it is called the backward Kolmogorov equation.
$$ \frac{\partial p}{\partial t’} + c^2 \frac{\partial^2 p}{\partial y’^2} =0 $$
4. Solve the Forward Kolmogorov Equation
We will solve for p right now! However, we will solve it by assuming similarity solution.
$$ \frac{\partial p}{\partial t’} =c^2 \frac{\partial^2 p}{\partial y’^2} $$
This equation has an infinite number of solutions. It has different solutions for different initial conditions and different boundary conditions. We need only a special solution here. The detailed process of finding that solution is showing as the following,
4. 1 Assume a Solution Form
$$ p=t’^a f(\frac{y’}{t’^b}) = t’^a f(\xi)$$
$$ \xi = \frac{y’}{t’^b}$$
, where a, and b are indefinite variables.
Again, don’t ask why it is in this form, because it is a special solution!
4.2 Derivation
$$\frac{\partial p}{\partial y’}=t’^{a-b}\frac{df}{d\xi}$$
$$\frac{\partial^2 p}{\partial y’^2}=t’^{a-2b}\frac{d^2f}{d\xi^2}$$
$$\frac{\partial p}{\partial t’}=at’^{a-1}f(\xi)+by’t’^{a-b-1}\frac{df}{d\xi}$$
Substitue back into the forward Kolmogorov equation (remember y’ = t’^b \xi), we get,
$$ af(\xi) – b\xi \frac{df}{d\xi} = c^2 t’^{-2b+1} \frac{d^2f}{d\xi^2}$$
4.3 Choose b
As we need the RHS to be independent of t’, we could choose the value of b=\frac{1}{2}, to let the t’ has a power of 0. Why we do that? Because we aim to reduce the partial differential equation to be a ordinary differential equation, in which the only variable is \xi, and t’ disappear.
By assuming the special form of p, and letting b= 1/2, our forward Kolmogorov becomes,
$$ af(\xi) – \frac{1}{2}\xi \frac{df}{d\xi} = c^2 \frac{d^2f}{d\xi^2}$$
$$ p=t’^a f(\frac{y’}{\sqrt{t’}}) = t’^a f(\xi)$$
$$ \xi = \frac{y’}{\sqrt{t’}}$$
4.4 Choose a
$$p=t’^a f(\frac{y’}{\sqrt{t’}}) $$
We know that p is the transition p.d.f., its integral must be equal to ‘1’. t’ is independent by the definition of random walk behaviour, so we do only integrate p, w.r.t. y’.
$$\int_{\mathbb{R}}p\ dy’ = \int_{\mathbb{R}} t’^a f(\frac{y’}{\sqrt{t’}})\ dy’ = 1$$
$$ \int_{\mathbb{R}} t’^a f(\frac{y’}{\sqrt{t’}})\ dy’ = 1 $$
, by replace x = \frac{y’}{\sqrt{t’}},
$$ \int_{\mathbb{R}} t’^{a+1/2} f(x)\ dx =t’^{a+1/2} \int_{\mathbb{R}} f(x)\ dx= 1 $$
$t’$ is independent, so the above equation would be equal to ‘1’ regardless the power of $t’$. Thus, $a = -\frac{1}{2}$ for sure.
Also, we get \int_{\mathbb{R}} f(x)\ dx= 1.
4.5 Integrate! Solve it!
By assuming the special form of p, and letting a=-1/2, b=1/2, we get,
$$ -\frac{1}{2}f(\xi) – \frac{1}{2}\xi \frac{df}{d\xi} = c^2 \frac{d^2f}{d\xi^2}$$
$$ p=\frac{1}{\sqrt{t’}} f(\frac{y’}{\sqrt{t’}}) = \frac{1}{\sqrt{t’}}f(\xi)$$
$$ \xi = \frac{y’}{\sqrt{t’}}$$
The forward Kolmogorov equation becomes,
$$ -\frac{1}{2}\bigg(f(\xi) – \xi \frac{df}{d\xi} \bigg)= c^2 \frac{d^2f}{d\xi^2}$$
$$ -\frac{1}{2}\bigg( \frac{d \xi f(\xi)}{d \xi} \bigg)= c^2 \frac{d^2f}{d\xi^2}$$
, as f(\xi) – \xi \frac{df}{d\xi} = \frac{d \xi f(\xi)}{d \xi}.
Integrate 1st Time
$$ -\frac{1}{2}\xi f(\xi)= c^2 \frac{df}{d\xi} + constant$$
There’s an arbitrary constant of integration that could go in here but for the answer we want this is zero. We need only a special solution, so we can set that arbitrary constant term be zero.
So, the eq could be rewritten as,
$$ -\frac{1}{2c^2}\xi d\xi = \frac{1}{f(\xi)}df $$
Integrate 2nd Time
$$ ln\ f(\xi) = -\frac{\xi^2}{4c^2} + C$$
Take exponential, f(\xi) = e^C e^{-\frac{\xi^2}{4c^2}} = A e^{-\frac{\xi^2}{4c^2}} .
Find A
The Last Step here is to find the exact value of A. A is chosen such that the integral of f is one.
$$\int_{\mathbb{R}}f(\xi)\ d\xi =1$$
$$ \int_{\mathbb{R}}A e^{-\frac{\xi^2}{4c^2}} \ d\xi = 2cA\int_{\mathbb{R}} e^{-\frac{\xi^2}{4c^2}} \ d\big(\frac{\xi}{2c}\big) =1 $$
$$ 2cA \sqrt{\pi} = 1 $$
, so we get A = \frac{1}{2c\sqrt{\pi}}
Plug f(\xi), a, b, A back into p = t^a f(\xi).
$$ p(y’)=\frac{1}{2c\sqrt{\pi \ t’}}e^{-\frac{\xi^2}{4c^2}} =\frac{1}{2c\sqrt{\pi \ t’}}e^{-\frac{y’^2}{4c^2t’}} $$
$p(.)$ now is normal like distributed.
$$N(x) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$$
So, we may say \mu_{y’}=0, and \sigma^2_{y’}=2c^2t’. Or, y’ \sim N(0, 2c^2t’).
5. Summary
$$p(y’)=\frac{1}{2c\sqrt{\pi \ t’}}e^{-\frac{\xi^2}{4c^2}} =\frac{1}{2c\sqrt{\pi \ t’}}e^{-\frac{y’^2}{4c^2t’}} $$
Finally, we solved the transition probability density function p(.). By assuming the forward or backward type of trinomial model, we find a partial differential relationship. Then, assuming a special form of p(.) by similarity method, we solve it.
The meaning is that p(y’)=\frac{1}{2c\sqrt{\pi \ t’}}e^{-\frac{\xi^2}{4c^2}} =\frac{1}{2c\sqrt{\pi \ t’}}e^{-\frac{y’^2}{4c^2t’}} is one of the transition probability density function that can satisfy the trinomial random walk.
Also, we find that p(.) is normally liked distributed.
因子投资的高维数时代
摘要:实证资产定价已然进入因子(协变量)的高维数时代。本文抛砖引玉,阐述我对此的四点思考。(DGP: Data Generating Process)
- Key Takeaway: over-parameterization 的时代已经到来,变量数量 k 大于样本数量 t 似乎并没有带来 interpolate的问题,反而给prediction带来了帮助。
0 引子
时至今日,实证资产定价(以及因子投资)已然步入了因子(协变量)的高维数时代。大量发表在顶刊上的实证结果表明,多因子模型具有很大的不确定性且因子的稀疏性假设不成立。人们熟知的 ad-hoc 简约模型无法指引未来的投资。
在高维数时代,寻找真正能够预测预期收益率的协变量是核心问题之一。为了实现这个目标,需要考虑的问题包括:(1)多重假设假设检验;(2)投资者(高维)学习问题 & 另类数据;(3)来自资产定价理论的指引:即解释预期收益率的因子应该也能解释资产的共同波动。最后,一个最新的讨论热点是因子的个数是否越多越好(即模型复杂度是否越高越好):复杂模型能更好地逼近真实 DGP,但参数估计的方差更大;简约模型的参数估计更准确,但却未必是 DGP 的合理近似。二者相比,如何权衡呢?
近日,我在某券商 2023 的年度策略会上做了题为《因子投资的高维数时代》的报告,阐述了我对上述四点的思考。本文借着报告的 slides 做简要介绍。由于对于某些问题专栏已经做了大量的梳理(比如多重假设检验),因此在本文的阐述中,在必要的地方会使用最少的文字(你马上就会明白我的意思)。
1 多重假设检验
这部分,一图胜千言。需要相关知识的小伙伴,请查看公众号的《出色不如走运》系列。
Next.
2 投资者学习问题 & 另类数据
理性预期假设投资者知道真实的估值模型。
然而,和进行事后(ex post)因子分析的你我一样,投资者在投资时同样面临协变量的高维数问题,因此不可能知道真实的估值模型,所以理性预期假设并不成立。这造成的结果是,均衡状态下资产价格和理性预期情况下相比出现偏差。在事后分析中,已实现收益率中包含一部分因估计误差导致的可预测成分。但对投资者来说,事前(ex ante)无法利用上述可预测性。
因误差导致的可预测性能够在样本内(IS)产生虚假的可预测性(无论投资者是否使用了先验以及无论先验是否正确),而在样本外(OOS)却无法预测收益率。这就是投资者(高维)学习问题导致的虚假的可预测性(Martin and Nagel 2022)。具体阐述见《False In-Sample Predictability ?》。面对这个问题,需要通过 OOS 检验才能规避。

投资者无法在事前投资中应对高维数,这主要体现在他们使用较少的协变量(因子)作为估值的依据。另一方面,由于一些变量的获取成本很高,投资者需要在该变量带来的预测好处和其成本之间权衡。此外,有限理性中的有限注意力机制也为投资者对简约性的渴望提供了微观基础。这两方面作用合力导致投资者在为资产定价时使用过度稀疏的估值模型。这样做的后果是,即便在样本外,也会出现因投资者学习问题而造成的虚假的可预测性。
就着上述推论,我们自然地引出本小节的另一个相关话题:另类数据。
回忆一下公众号之前的文章《科技关联度II》所介绍的 Bekkerman, Fich and Khimich (forthcoming)。相比于之前的基于专利类别的研究,该文对专利进行文本分析,通过提取专业术语并计算其重合度来描述公司之间的相似程度,以此构造了预期超额收益率更高的科技关联度效应。
比起专利类别,投资者在获得以及处理专利文本并计算科技关联度时的成本更加昂贵。这会导致大多数投资者会在为公司估值时忽略这方面的信息,即使用过度稀疏的估值模型,造成样本内和样本外收益率可预测性。
该文基于文本分析的科技关联度是近几年大红大紫的基于另类数据进行实证资产定价和因子投资的一个典型例子。然而,Martin and Nagel (2022) 所勾勒出的非理性预期假设世界告诉我们,使用最新的方法和技术构建预测变量并将其应用于早期历史时段时,它们在样本内和(伪)样本外检验中均能预测预期收益率。因此,我们在惊喜于另类数据的发现之余,恐怕也应该多一分谨慎。
除此之外,既然谈到另类数据,不妨再聊聊另一个相关话题。有相关研究表明,海外大量的另类数据供应商提供的数据都只具备对公司基本面的短时间尺度的可预测性。Dessaint, Foucault and Fresard (2020) 的研究表明,如此另类数据可得性的提升降低了进行短时间尺度的预测成本(从而提高了准确性),但增加了进行长时间尺度预测的成本(从而降低了准确性)。对于公司基本面预测来说,二者的综合效果是 mixed。可以预见,未来在使用另类数据预测公司基本面时,会有更多的研究向这个方向倾斜。
3 和协方差矩阵有关
Ross (1976) 的 APT 指出,解释资产预期收益率截面差异的因子应该同时能够解释资产的共同运动。在市场中不存在近似无风险套利机会这个假设下,Kozak, Nagel and Santosh (2018) 同样论述了这一点(见《Which beta (III)?》)。
以下展示了 BetaPlus 小组构造并维护的 A 股常见七类风格因子在 2000/01/01 到 2022/04/30 之间的表现。统计数据表明,在该实证区间内,虽然它们的收益率均值高低有差异,但收益率的标准差同样也有差异,因此并没有哪个风格因子的风险调整后收益明显高于其他的因子。
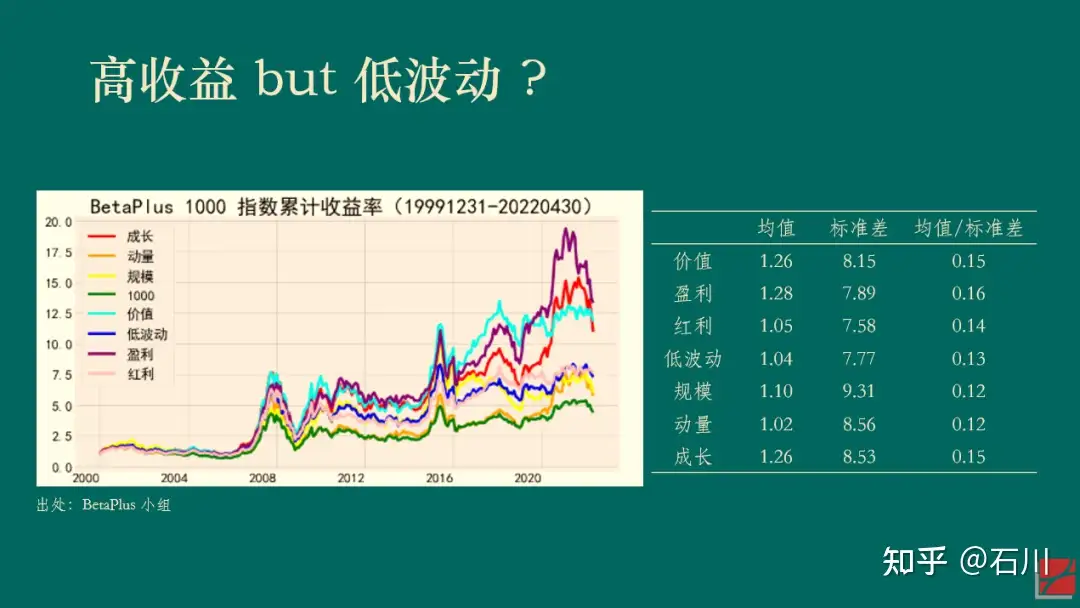
再来看一个美股的例子。Kozak, Nagel and Santosh (2018) 将实证区间分成前后两半儿并考察了 15 个因子。下图展示了每个因子在前后两个区间内夏普率的散点图。如果能够在获得高收益的同时降低波动,那么样本内(前一半区间)夏普率高的因子在样本外(后一半区间)的夏普率应该仍然更高一些,我们将会看到这些点围绕在 45 度直线上。然而事实并非如此。无论样本内的夏普率多高,这 15 个因子样本外的夏普率几乎是一条平行于横坐标的水平线,而非人们期望的 45 度斜线。(我用几百个因子在 A 股做了同样的实证,观察到了类似的结果。)
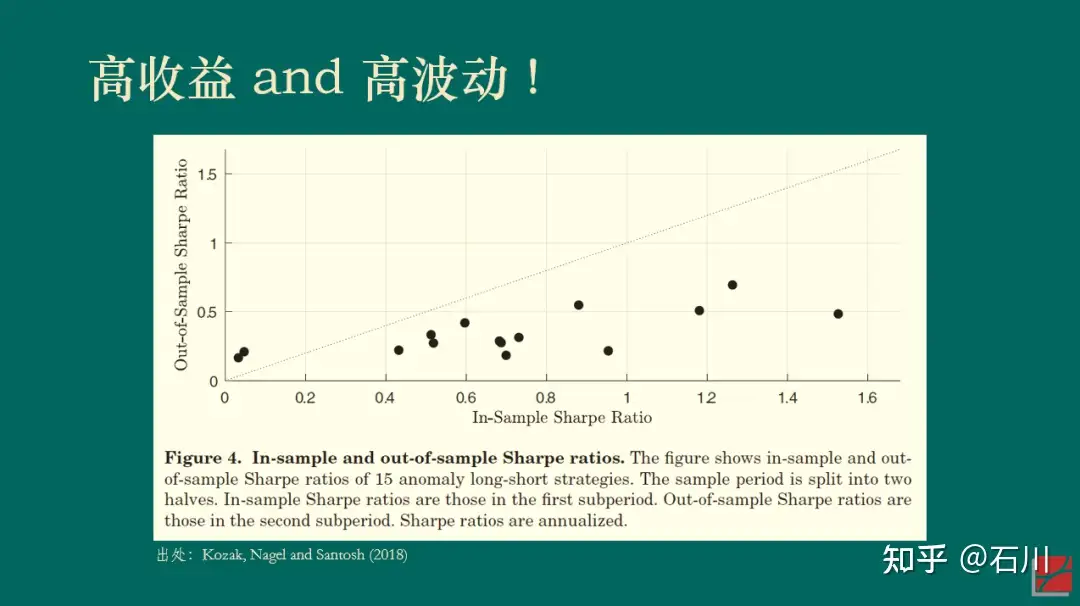
上述结果显示,(样本外)高收益往往对应着高波动(对着样本内硬挖 —— data snooping —— 另说),这一实证结果和 APT 吻合。
早在几十年前,Eugene Fama 曾经打趣到 APT 让众多挖因子的尝试“合理化”,即 APT 只说了资产预期收益率和众多因子有关,但却没有指出到底有哪些因子。因此,很多学者打着 APT 的旗号“肆无忌惮”地挖出了一茬又一茬因子(zoo of factors),Fama 把这个现象称作 APT 给了这些研究“fishing license”(即 APT 让这些研究合理化)。(Sorry,这里我实在忍不住吐槽一句,在一本著名的资产定价教材的中译版中,中文作者竟然真的把 fishing license 翻译成“钓鱼许可证”……)
如今,当我们重新审视 APT 时,毫无疑问应该将它作为挖掘真实因子的有效指引,正如本节一开头说的那样:解释资产预期收益率截面差异的因子应该也能解释资产的共同运动。在这个认知下,以 PCA 为代表的一系列实证资产定价研究在这几年取得了很多突破(Kelly, Pruitt and Su 2019 、Kozak, Nagel and Santosh 2020)。
4 越复杂越好 ?
在本节的讨论中,我们以因子个数的多少代表模型复杂度。因子个数越多,模型越复杂。
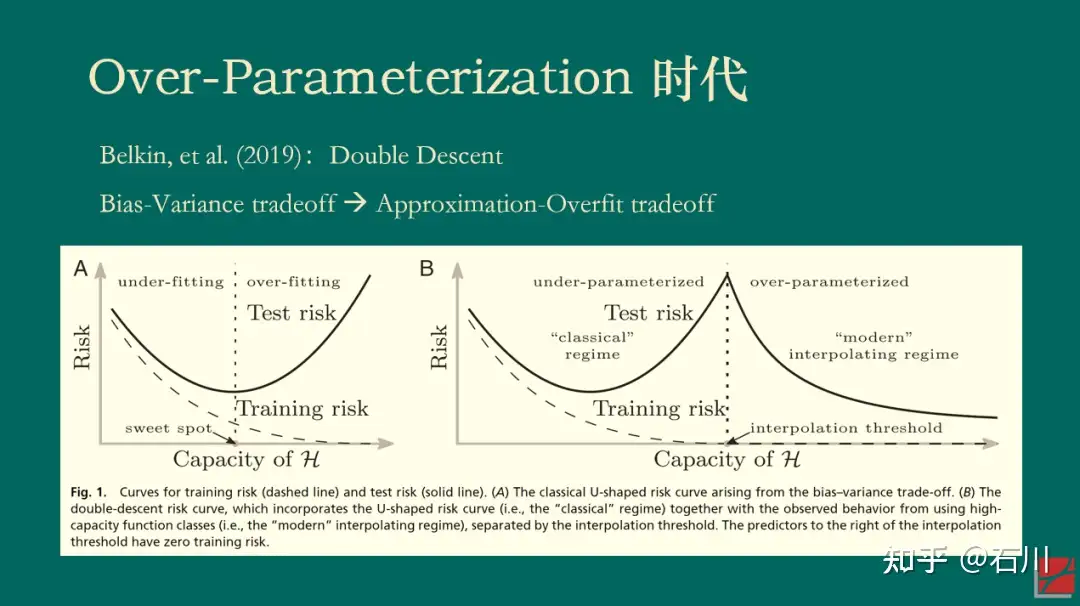
2019 年,Belkin, et al. (2019) 一文提出了机器学习中样本外误差的“double descent”现象,引发了机器学习领域和理论统计领域的广泛讨论。为了理解这一现象,我们先从熟知的 bias-variance trade-off 说起。
对于模型来说,其样本外表现和模型复杂度关系密切。当模型复杂度很低时,模型的方差很小(因为变量参数估计的方差很小),但是偏差很高;当模型复杂度高时,模型的方差变大,但是偏差降低。二者的共同作用就是人们熟悉的 U-Shape,即 bias-variance trade-off,因此存在某个最优的超参数,使得样本外的总误差(风险)最低。
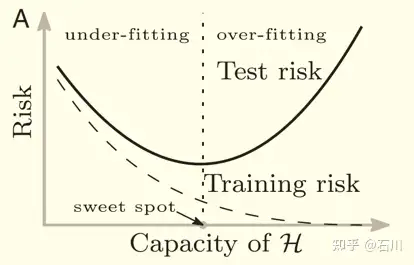
我们还可以换个角度来理解 bias-variance trade-off,而这个角度对理解 double descent 至关重要。当模型很简单时,它能够有效规避过拟合,但却很难想象如此简单的模型是真实世界的好的近似;而当模型复杂时,它更有可能逼近真实世界,但是也的确更容易过拟合。因此 bias-variance trade-off 也可以理解为 approximation-overfit trade-off。
然而,上述结论有一个我们都习以为常的前提:变量个数 < 样本个数。那么,如果模型复杂到变量(因子)的个数超过了样本的个数又会出现怎样的情况呢?事实上,这一问题并非无缘无故的凭空想象。对于复杂的神经网络模型来说,模型参数的个数很容易超过样本的个数,然而这些模型确在样本外有着非凡的表现(哦,当然不是资产定价领域)。这个现象促使这人们搞清楚 what is behind the scene。
当变量个数 > 样本个数时,模型在样本内能够完美的拟合全部样本(在机器学习术语中,这个现象被称为 interpolation)。对这样一个模型来说,人们通常的认知是,它在样本外的表现一定会“爆炸”,即毫无作为。这是因为它过度拟合了样本内数据中的全部噪声。然而,Belkin, et al (2019) 指出,当人们让模型复杂度突破样本个数这个“禁忌之地”后,神奇的事情发生了:样本外总误差并没有“爆炸”,而是随着复杂度的提升单调下降。正因为在样本个数两侧都出现了误差单调下降的情况,Belkin, et al (2019) 将这个现象称为 double descent。
因为本文的目的并非解释背后的统计学理论,所以我在此对该现象给一些直觉上的解释。当变量个数超过样本个数的时候,样本内的解是不唯一的,而最优的解可以理解为满足参数的方差最小(正则化或 implied 正则化在这个过程中发挥了非常重要的作用)。随着变量越来越多,最优解的方差总能单调下降。
再来看偏差,通常来说,偏差确实会随着复杂度的提升而增加。但是所有模型都是真实 DGP 的某个 mis-specified 版本。当存在模型设定偏误的时候,可以证明当变量个数超过样本个数时,偏差也会在一定范围内随着复杂度而下降。因此,二者的综合结果就是模型在样本外的误差表现会随复杂度的上升而下降。(在一些情况下,样本外误差的 global minimum 出现在当变量个数 > 样本个数时。)
以下两张 slides 总结了上面的话(第二张 slide 里的表参考了 Bryan Kelly 的 talk,特此说明)。


对于资产定价和因子投资来说,如果你和我一样认同因子的高维数时代 —— 即收益率的 DGP 包含了非常多的因子,那么上述关于模型复杂度的探讨也许会带来全新而有益的启发。在这方面,也有大佬已经走在了前面。Bryan Kelly 和他的合作者以及学生一起写了一系列“复杂度美德”的 working papers,在资产定价领域探索提升复杂度带来的样本外好处。例如,Kelly, Malamud and Zhou (2022) 一文使用神经网络对美股进行了择时(每次建模仅利用一年 12 期的数据训练神经网络),并发现了类似的 double descent 现象。
当然,即便我们认同了“越复杂越好”,也依然要回答更重要的问题,即如何估计参数,如何正则化,如何来利用成千上万甚至更多的因子来形成关于预期收益率更好的预测。虽然 Kelly 等人的文章在择时方面取得了让人兴奋的结果,但在 cross-section 是否有类似的实证结果依然需要时间来回答(Kelly 有一篇 working paper 研究 cross-section,但还没有 publicly available)。
但是无论如何,欢迎来到 over-parameterization 时代。
5 结束语
以上就是我对因子投资高维数时代的四点思考。
不过在本文的最后,仍然有必要指出,在协变量的高维数时代,如何 prepare 因子固然重要(小心多重假设检验、小心投资者学习、利用 APT 的 implication),但是如何求解高维问题才更加核心(如何利用复杂度的好处 ?)。
或许,我们已经到了从计量经济学到机器学习的必然转型时刻。正如 Stefan Nagel 的《机器学习与资产定价》(Nagel 2021)所倡导的那样,将经济学推理注入机器学习算法将成为高维数时代研究的必经之路。

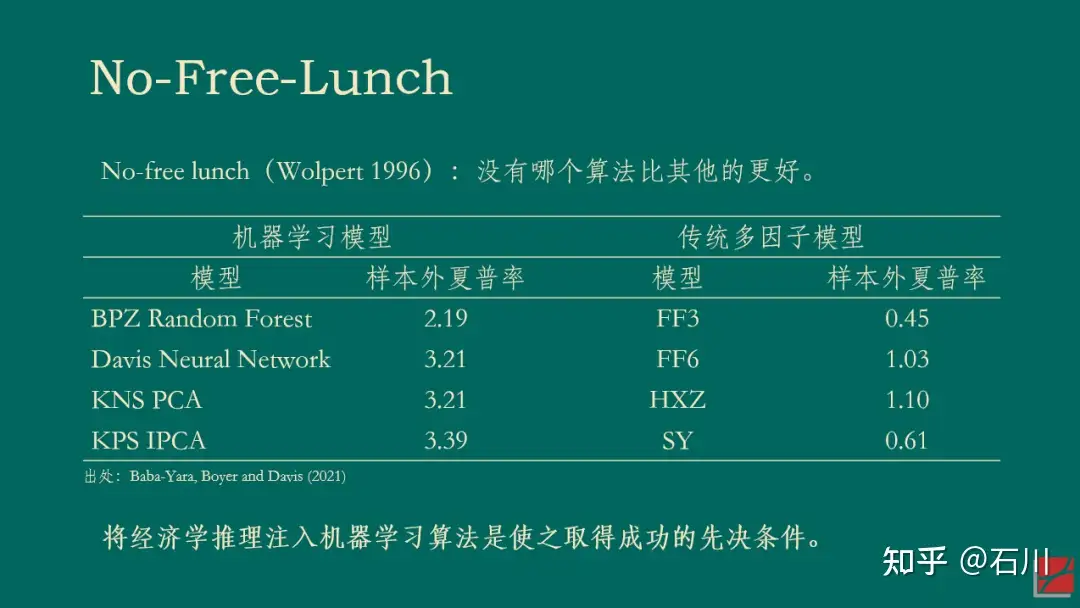
参考文献
- Baba-Yara, F., B. Boyer, and C. Davis (2021). The factor model failure puzzle. Working paper.
- Bekkerman, R., E. M. Fich, and N. V. Khimich (forthcoming). The effect of innovation similarity on asset prices: Evidence from patents’ big data. Review of Asset Pricing Studies.
- Belkin, M., D. Hsu, S. Ma, and S. Mandal (2019). Reconciling modern machine-learning practice and the classical bias-variance trade-off. PNAS116(32), 15849 – 15854.
- Dessaint, O., T. Foucault, and L. Fresard (2020). Does alternative data improve financial forecasting? The horizon effect. Working paper.
- Kelly, B. T., S. Malamud, and K. Zhou (2022). The virtue of complexity in return prediction. Working paper.
- Kelly, B. T., S. Pruitt, and Y. Su (2019). Characteristics are covariances: A unified model of risk and return. Journal of Financial Economics 134(3), 501 – 524.
- Kozak, S., S. Nagel, and S. Santosh (2018). Interpreting factor models. Journal of Finance73(3), 1183 – 1223.
- Kozak, S., S. Nagel, and S. Santosh (2020). Shrinking the cross-section. Journal of Financial Economics 135(2), 271 – 292.
- Linnainmaa, J. T. and M. R. Roberts (2018). The history of the cross-section of stock returns. Review of Financial Studies31(7), 2606 – 2649.
- Martin, I. and S. Nagel (2022). Market efficiency in the age of big data. Journal of Financial Economics145(1), 154 – 177.
- Nagel, S. (2021). Machine Learning in Asset Pricing. Princeton University Press.
- Ross, S. A. (1976). The arbitrage theory of capital asset pricing. Journal of Economic Theory 13(3), 341 – 360.
By
石川 https://zhuanlan.zhihu.com/p/589370949?utm_medium=social&utm_oi=774013724896788480&utm_psn=1583185642497994752&utm_source=wechat_session&utm_id=0
安全与发展 – 高善文经济观察
背景
1991年苏联解体以后,全球经济进入了后冷战时代,后冷战时代突出的特点是全球经济经历了以增长和效率为导向,以开放和融合为手段,以猛烈的经济增长为结果的波澜壮阔的接近30年的经济增长。而这一增长过程中国无疑是最大的受益者之一。苏联解体以后,全球经济经历的差不多接近30年的波澜壮阔的全球化,深刻的改变了全球地缘政治的格局。
在这样的背景下,在最近几年以来,由于与全球化伴随的地缘政治环境的变化,以及许多国家内部政治经济环境的变化,安全开始成为许多政府企业和金融机构在思考增长和效率的同时,不得不认真考虑的关切。
而这样的安全关切在整个90年代,在2010年之前的十年,总体上并不明显。比如说作为现在的跨国公司的管理层,在考虑供应链的全球布局和生产能力的全球布局的同时,他要考虑效率,要考虑成本,但是现在同时也要考虑供应链的韧性,也要考虑备份,也要考虑安全冗余。
比如说许多国家的中央银行和大型金融机构在国际金融市场进行资产配置的时候,他要考虑在极端的条件下,自己的美元资产会不会遭遇像俄罗斯中央银行的外汇储备一样的结局?就是由于这样或者是那样的政治因素的话被冻结,甚至的话被没收,而在2020年之前,对大多数中央银行来讲,这样的安全关切应该说都是不突出的。实际上今年以来,在国际黄金价格的上涨过程之中,非常重要的持续的买家之一,就是许多国家的中央银行。那么为什么许多国家的中央银行在今年以来大量的增持黄金?众说纷纭,但是一种解释就是美国等西方国家冻结俄罗斯外汇储备的措施,使得其他中央银行在外汇储备的配置上要考虑安全冗余。
再比如说对于一些西方国家政府而言,在很多重要的技术领域都采取了额外的限制措施,这些限制措施通常被认为也反映了他们日益加剧的安全关切,所以安全与发展问题再继续追求经济增长的同时去兼顾安全关切,已经是一个在全球范围之内相当普遍的重要的关切。
在这样的条件下,我们看到二十大的报告非常正式的提出了安全与发展的主题,要统筹好安全与发展的关系,安全是发展的前提,发展是安全的保证,要这个妥善的统筹和处理好 安全与发展之间的关系。那么这一主题的提出毫无疑问反映了我们刚才所讲的很多国际国内政治经济环境的变化,但是从这一主题的提出到它最终落实为一整套庞大的政策法律法规体系,就是把这样的主题最后落实为一整套庞大复杂精巧的法律法规体系,无疑是需要时间的。而这一过程的话也会对于经济社会很活动,对于很多企业产生微妙的或者是十分重大的影响。
我们接下来讨论的问题的重点是想弄清楚在全球和中国都在统筹兼顾安全与发展的条件下,这样的时代主题的变化会如何的影响资本市场的估值体系,特别是如何影响资本市场的估值结构?那么呢我想了一段时间的话,试图提出一个概念性的框架性的分析思路,然后接下来我们会用一些案例去尝试去解释这个概念体系。但是毫无疑问的话,随着未来的政策法律法规体系变得越来越细致,越来越精巧,我们还可以补充越来越丰富的案例,然后的话我们有一些案例也不见得那么恰当,需要继续调整。
安全 x 发展
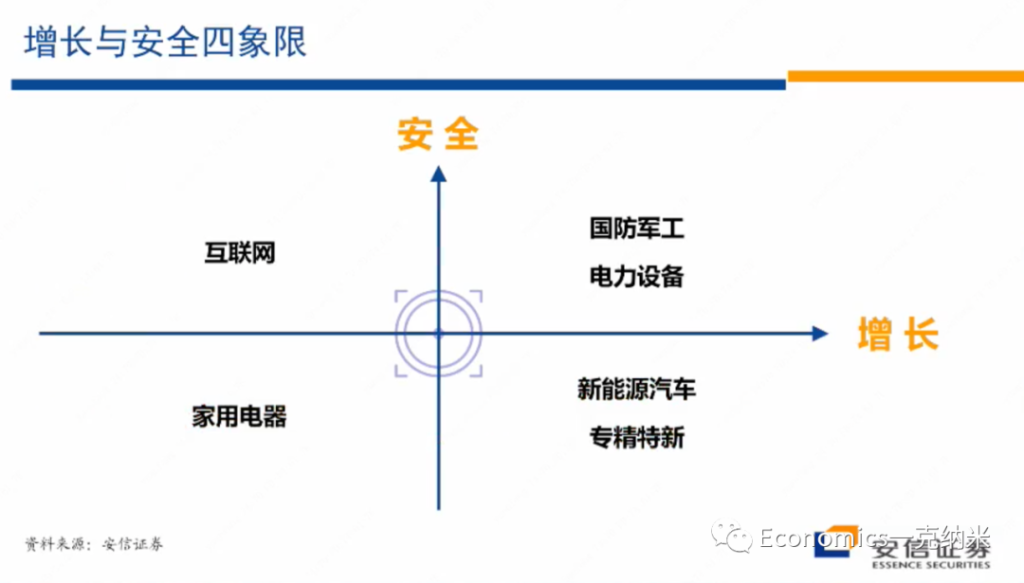
$$ 安全 \times 增长 $$
所以在这里我首先想跟大家介绍的是个人思考了一段时间以后所想提出的一个分析的概念体系,或者是基本的分析思路。我的基本的想法的话是可以设立一个两维四象限的坐标体系,它的横轴的话是增长的纬度,纵轴的话是安全的维度。那么在四象限体系之中,在横轴上越往左边走,那么一个给定的行业或者是一个给定的企业,它的增长动力、增长潜能、增长潜力就越弱,越往右边走的话,它的增长的潜力,增长的动力相对而言的话就越强。然后在纵轴上的话是安全关切,所以的话在纵轴的下方,应该说它标志着与它相关联的很多的行业,不很涉及到安全关切,对它的安全关切的维度,或者是对安全的影响相对是很小的,在纵轴上越向上方走,那么安全关切越严重,安全关切的越大。
然后我们还想说的是我们在这里所说的安全理论上应该是一个总体的安全观,它应该包括比如说金融安全、经济安全、生态安全、领土安全、政治安全、意识形态安全等等。政府的安全关切是一个总体的安全关切,所以的话在这样的安全关切下的未来将要制定的政策法律法规体系,也必然反映了具有非常广泛含义的一个安全主题,那么与这样的一个背景相适应,我们在这里所想讲的纵轴的安全问题,也是一个相对综合的总体的安全关切。
Specify
那么有了这样的一个四象限的划分以后,我们试图在四象限里边的话举出一些案例,这些案例不尽恰当,但是的话一部分原因的话是因为我们认为在过去几年反映了安全关键的变化,在这些层面上的话已经有一些政策上的进展,另外一方面这些案例有助于说明我们即将这个展开的逻辑。
- Debt – Gov Bond <- for Safety
- 我们从横轴来看问题,从横轴来看问题。在中国的资本市场上的话,我们知道通常有一个大拇指法则,如果你要买债的话,在公司基本面一样的背景下,你要买国有企业的债,如果这两个公司的基本面是差不多的,你要买国有企业的债,原因也很简单,一方面的话国有企业本身经营更加稳健,当然不排除有很多稳健的民营企业,但是国有企业总体上经营更加稳健,另外一个的话就是在行业遭受意想不到的负面因素的影响和困难的条件下,总体上国有企业获得政府救助的可能性不低于民营企业,也许比民营企业要大一些,所以在同样的条件下,我们一般认为要买国有企业的债。
- Equity – Public Issued Private Firm <- for Growth
- 那么另外一个的话,如果在股票市场上,在公司的基本面差不多的条件下,你要买民营企业的股票,要买民营企业的股票,重要的原因之一,也是相对而言,国有企业的经营太稳健,风险暴露不足,而民营企业的话具有更多的增长方面的追求,从而更好地匹配了股票投资者对增长和风险暴露的要求。
那么从横轴来看,一个常常看到的现象,在相对低增长的行业里边,整个的经营环境比较稳定。那么国有企业相对而言的话可以有不错的生存环境,如果市场是竞争性的,然后的话是可以相对自由进出的,但是在一个高速增长的技术非常不确定充满变化的行业之中,总体上来讲,国有企业的优势相对民营企业而言不是那么突出。
Quadrant
那么有了这样的背景介绍以后,我们来介绍一下我们对4个象限里边它的一个主要的影响的看法。
- 第一象限:
- 无疑的话它满足两个特征,第一个特征的行业是高增长状态,第二个的话它与安全关切密切相关,典型的比如说卡脖子工程,典型的比如说涉及到国防军工等等很敏感的领域,典型的比如说事关未来制造业尖端的竞争力的核心技术。
- 在这些领域的话,它既有非常大的一个增长的不确定性和潜力,同时又事关安全关切。那么在这个领域毫无疑问的话,我个人认为的话,未来所谓的新型举国体制将要重点发力的领域,就是在第一象限,那么新型举国体制在第一象限怎么发力?我们还需要继续观察。但是我个人认为的话,在这一象限之中,一个非常大的矛盾是如果在象限之中完全由国有企业来主导,那么由于国有企业本身经营相对比较稳健,面对高速增长和不断变化的技术环境,它不见得能够去抓住和实现很多不同的技术路径去实现最终真正市场驱动的增长。但是如果在这个领域完全由民营企业去主导,那么民营企业的主导在多大程度上能够很好地解决安全关切,也是存在一些需要继续观察的一些现象的。那么在这个领域,我现在倾向性的想法是这个领域在未来一定是国有企业和民营企业并重,两个毫不动摇。政府一方面要支持民营企业在这一领域能够非常自由的去去实现增长,去创业、去研发。另外一方面,毫无疑问的话,也会支持国有企业在这一领域的话做大做强。特别重要的是在这些领域,如果潜在的在众多的细分的小的行业和领域里边,一个企业可以做到龙头,但是在细分行业的龙头在总量上在宏观上不具有足够大的体量,那么在这些领域我个人猜测可能民营企业的优势相对会更多一些。但是如果一个行业本身具有战略性的全局性的重要性,企业的体量在未来有足够的大,那么国有企业或者是国有的成分在其中,很可能的话将是十分重要的。
- 民营负责增长,国有负责做大做强
- 第二象限
- 第二象限的两个特征:1. 有安全关切,2. 没有增长,没有增长意味着行业的竞争格局、技术路径、用户市场等等的话相对比较稳定。在政府全面加强监管和管制的条件下,在这一领域,在整个的行业的增长环境相对比较稳定的条件下,国有企业总体上来讲的话会获得一些优势,或者如果政府不用监管和管制的手段去管理这些行业,那么另外一个办法就是扩大国有企业的话在这些领域的存在。
- 有安全需求,意味着拒绝外资,存在行业壁垒,国企垄断。市场稳定,无竞争,无增长。
- 第三象限
- 既没有增长,同时又不关安全关切。那么在这一领域政府会继续延续以前长期坚持的政策,会继续毫不动摇的鼓励民营企业在这些领域的话去做大做强,会继续去欢迎外资和外商在这些领域去投资和展业。
- 在我们在这里举了一个家用电器的例子,实际上另外一个例子,比如说资产管理,比如说公募基金,那么在一定程度上,也许它也可以放在象限,它没有那么大的安全关切,同时的话行业的竞争格局在一定程度上也比较成熟和稳定。
- 政府在这个领域继续去扩大开放,引进外资,对民营企业的话采取公平竞争,甚至是更照顾性的政策。在这个领域破除行政性的垄断,去鼓励竞争,延续过去很多年的政策,都是完全可能的。
- 由于没有安全的需求,可以吸引外资。由于没有增长,鼓励竞争促进增长。 – 惨烈,但在竞争中脱颖而出的企业可能有巨大机会。
- 第四象限
- 涉及到未来相对比较强劲的增长,同时它的安全关切又不大。这些领域的话毫无疑问由于增长所暗含的技术以及商业环境变动的不确定性,以及它的安全关切没有那么大,民营企业将是在这一领域的话最为主导性的力量。
- 但是对比第三和第四象限非常重要的区别是在第三象限,对第三象限的行业和企业而言,可以继续坚持全球化的路径,可以继续坚持全球化的供应链的配置,全球的市场的开放和竞争。
- 对于第四象限的行业和企业而言,是不是包括专精特新存在争议,比如说太阳能光伏等等的领域,比如说新能源汽车。一般认为是存在高增长的领域,安全关切又不是那么严重,它应该继续可以维持一个全球开放包容互联互通的贸易体系,让中国的企业的话继续在全球市场上做大做强,去参与竞争。但是这些领域的问题是看起来,包括美国欧洲在内,也试图在这些领域采取一些或者说是限制性的政策,或者是对本国企业的话进行扶持性的政策,从而扭曲全球的竞争环境。
3C
我们知道美国政府所谓的对华政策有三C 的说法,其中的话一个C 是corporation是合作,那么在第三象限的,我认为在经济上的话,在这个领域中美之间的合作应该是没有什么障碍的。
还有一个C 的话是competition就是竞争,这个竞争的话当然是良性的竞争,那么在竞争这一领域,也许它适用于第四象限的情况,比如说美国政府试图去补贴他们的电动汽车行业,希望与中国的电动汽车企业进行竞争,去也许去补贴他们的一些民用的具有潜在高增长的领域的行业,与中国的企业进行竞争。但是在这个领域的主要的问题,也许的话各国都试图通过补贴等等扭曲竞争的手段来获得一些优势,但是也许需要一些全球性的更加统一的贸易规则来管理在高增长的新兴领域在全球范围之内的竞争,但是在这些领域总是有一些空间的。
我们知道很多人担心中国的新能源汽车的高速增长的出口是不是能够维持,在很大程度上实际上背后的担心是美国是不是会像在半导体等等领域的政策一样,去对我们的新能源汽车进行打压。那么在我们这样的一个四象限的分析体系之中,我个人倾向于认为中美欧在一定程度上制定一些全球性的通用的管理补贴,管理竞争的规则,使得在这些领域的话,全球化能够继续推进全局性的一个合作和竞争,能够继续正常和健康的展开,可能性和空间应该是比较大的。
如果说第三象限就是美国人所讲的c之中的cooperation,那么第四象限也许就是良性的 Competition竞争,第一象限恐怕在一定程度上就是另外一个c。那么毫无疑问的话,围绕这些变化所带来的很多的政策法规体系,有一个逐步落地的过程,而且这一过程也难免会有很多的调整,纠偏会有很多的反复。
Cases
接下来,我们是想使用我们在这里所找出的几个案例,围绕我们刚才所讲的这些特征,来看一看市场是如何表现的,从而的话为我们未来进一步去理解这些过程对众多行业的影响提供一些线索。
- 第一象限 – 军工
我们计算的是国防军工指数的情况,国防军工的话毫无疑问它处在第一象限,处在第一象限,那么由于安全关键的增强等等,它相对它相对的增长前景的话变得更加明朗。
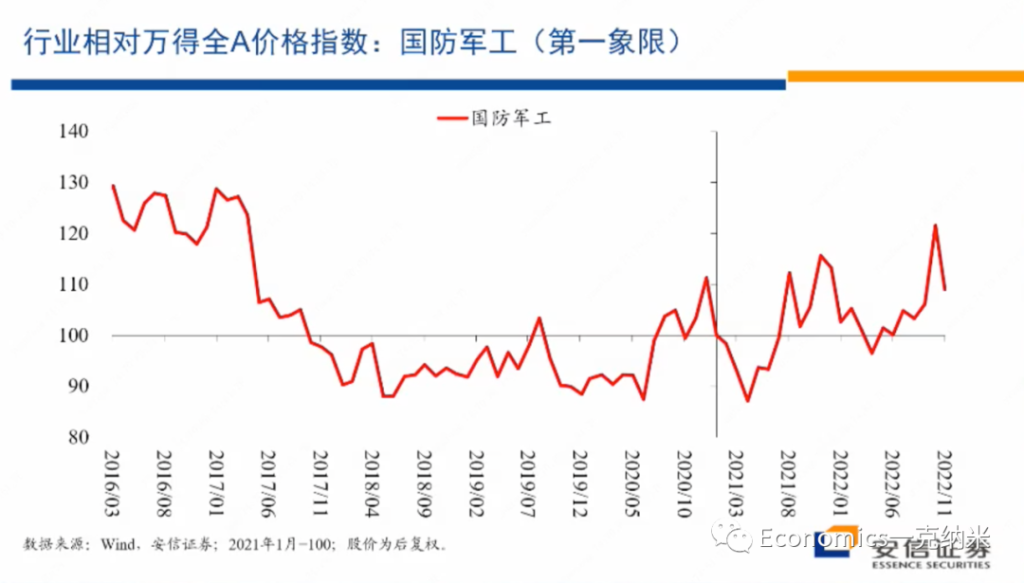
我们这张图使用的是国防军工相对于万德全A的价格指数,就是国防军工的价格指数除以万得全A的价格指数,然后某个时间点设定为100,然后我们来看它的变化。那么在这张图上很容易看到的,2020年的某个时候以来,相对于万得全A指数,总体上来讲,国防军工指数开始获得一个单边的,尽管有很多波动的越来越大的一个相对收益。
在国防军工指数获得相对收益的同时,我们再来看,在行业在国防军工这个行业之内,国有企业相对于非国有企业的估值情况,我们刚才说第一象限里边一方面它继续去维持增长,另外一方面在一些重要的领域,可能国有企业由于这样那样的原因会获得额外的优势,这种优势毫无疑问会反映在估值层面上。
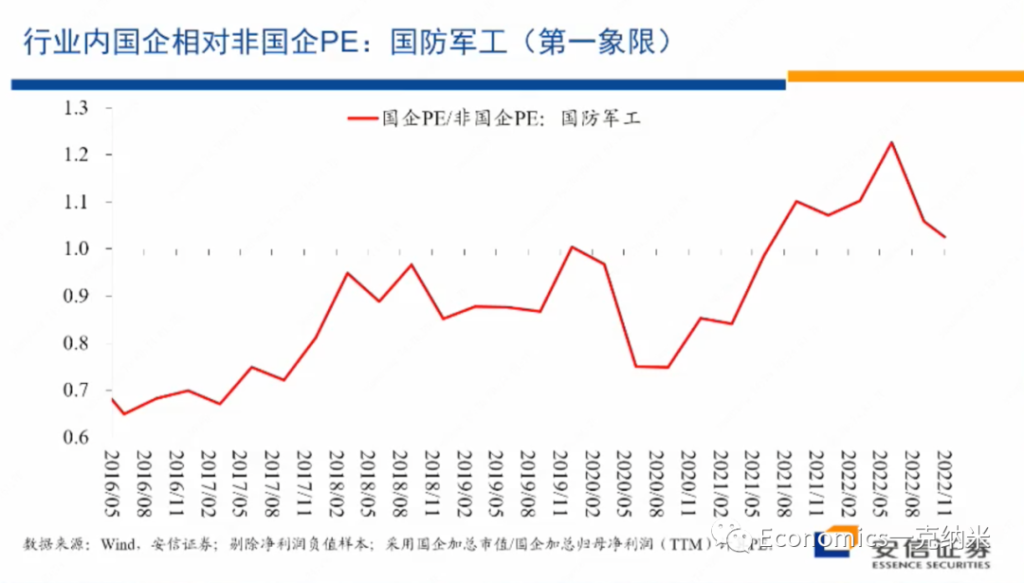
国防军工的估值在行业内相对非国有企业的情况如上图。那么结论也是类似的,跟我们刚才的阐述和预期比较接近。进入2020年以来,2020年七八月份以后,总体上在行业内国企相对非国企开始获得越来越大的估值优势。
在第一象限里边的国防军工行业,如果大家说国防军工获得相对外的权益,可能还有很多别的原因。但是在行业内部国企相对非国企获得了估值上的优势,提供了另外一个值得我们思考的证据,那么这个的话是从市净率的角度来考虑,从市净率的角度来考虑,相对的结论也是类似的。
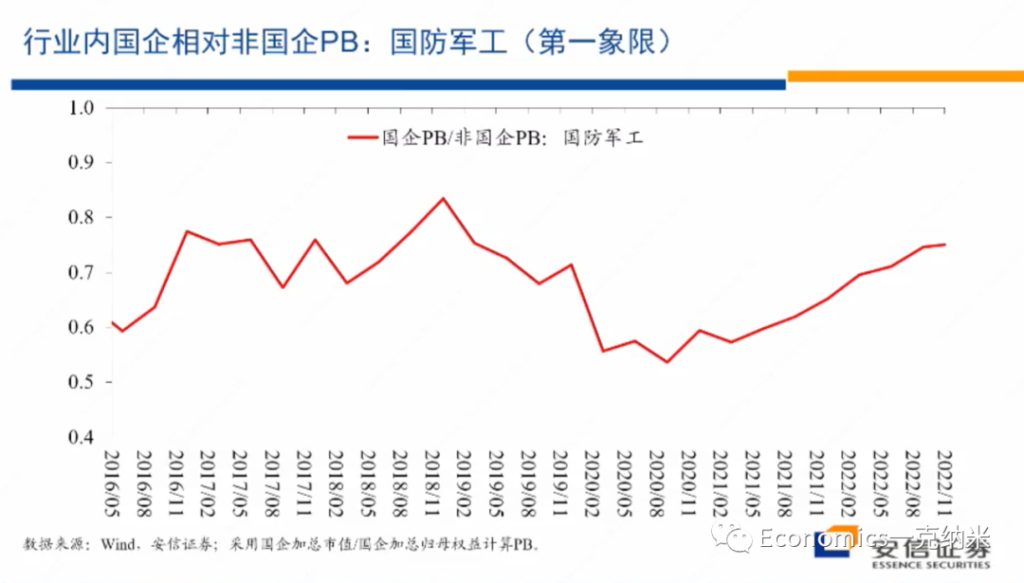
2020年以后,国企相对非国企的估值优势总体上正在出现相对单边的放大。对国防军工这样一个明显的处于在第一象限的行业来讲,第一它高增长或者是高增长再进一步得到加强。
再者,是电力设备。之所以把电力设备放在这里,是因为我不是那么拿得准电力设备在多大程度上是否涉及到安全关切,对一部分国外的一些观察家来讲,他们怀疑担心或者认为电力设备同样存在安全关切,因为他们担心其他国家的政府在发电设备里边会安装后门,这样的话当两国处于敌对状态的时候,通过开启后门是对方的供电网络整个瘫痪,这个就可以不战而屈人之兵。
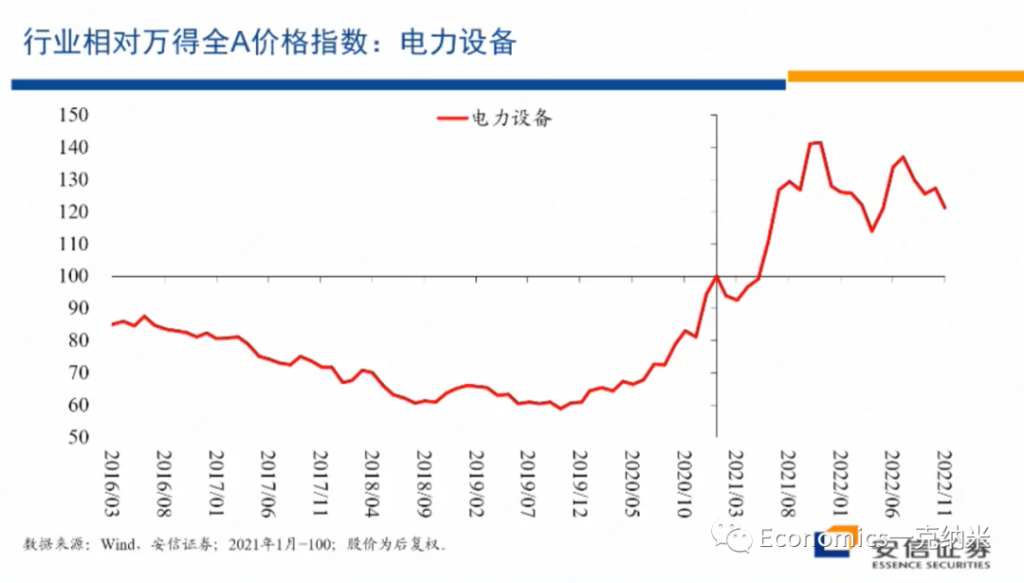
在这个意义上来讲,电力设备涉及到重要的基础设施,从而的话存在安全关切。但是到底如何看待电力设备这个行业,大家可以见仁见智,但是我们来看一看它的一个这个行业内的一个表现,一个的话是它相对万德全A的价格指数,我们看到进入2020年以后,总体上它具有明显的相对的收益。
另外在行业之内,国企相对非国企在2020年以后它的估值优势在扩大。2020年以后,2021年初以后,国企相对非国企的估值优势在扩大,特别是在市净率层面上,估值的扩大的表现的很明显,在市盈率层面上情况是相似的。
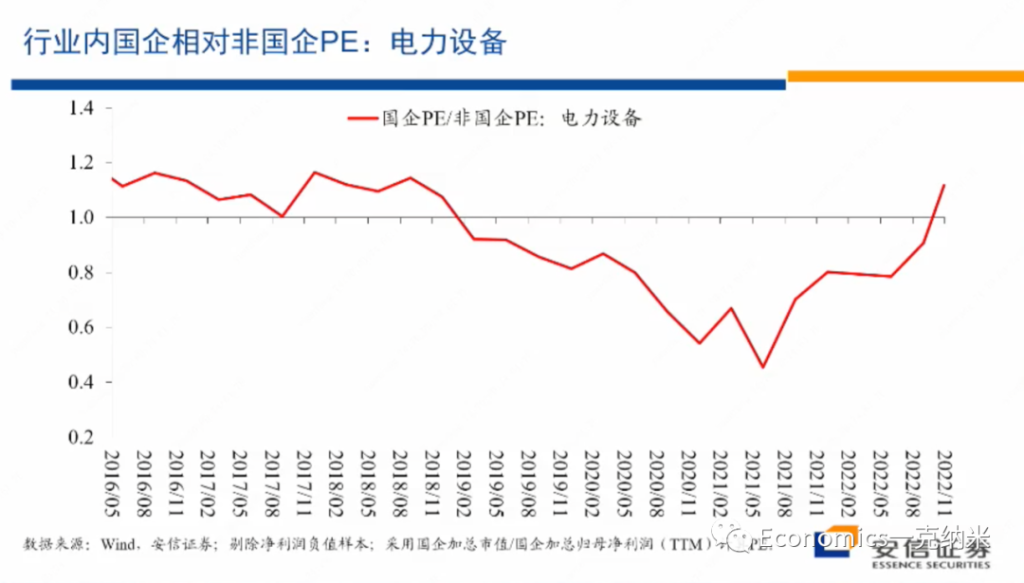
那么从它获得相对收益到国企获得相对估值优势这些层面上来讲,电力设备与国防军工都有一定的相似性,所以我们刚才把它放在了第一象限,但是这当然是可以争议的。
- 第二象限 – 互联网
进入第二象限,我们找的一个指数的话是wind中概股100指数的中概股,100指数里边的大头的话是互联网。当然除了互联网还有很多别的企业,但是大头是互联网。

这是一个相对宏观的指数,不完全是一个单个行业的指数。在反对资本无序扩张的过程之中,应该说互联网相对是资本无序扩张表现比较明显的一个领域。反对资本无序扩张,显然有安全关切在里边。而进入最近这几年以来的话,互联网的话毫无疑问的也结束了此前的高增长状态,转入的一个相对中低速的增长。
那么观察wind中概100指数的情况的话,毫无疑问的话就像大家都知道的一样,如果以纳斯达克指数为基准的话,我们看到进入2021年以后的话,它具有相对显著的价格上的走弱,同时他们的营业收入毫无疑问,特别是进入2022年以后,进入一个相对很低的增长阶段,这是它相对纳斯达克的一个估值的变化,市净率的估值的变化。
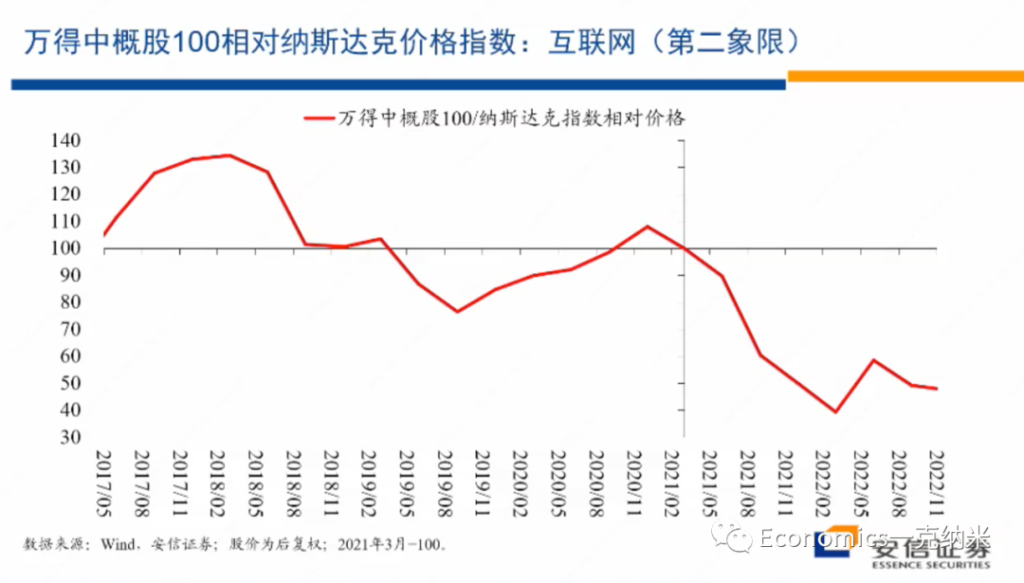
我们看到的在2018年之前它有一些估值的优势,随着高增长的结束,在2018年到2020年的它相对纳斯达克的估值是一样的。进入2021年以后,它相对纳斯达克的估值上的劣势开始逐步的放大。从政府对这些行业的管理措施来讲,非常细的法律法规体系似乎还没有看到,但是红绿灯体系已经是明确提出的一个标准。
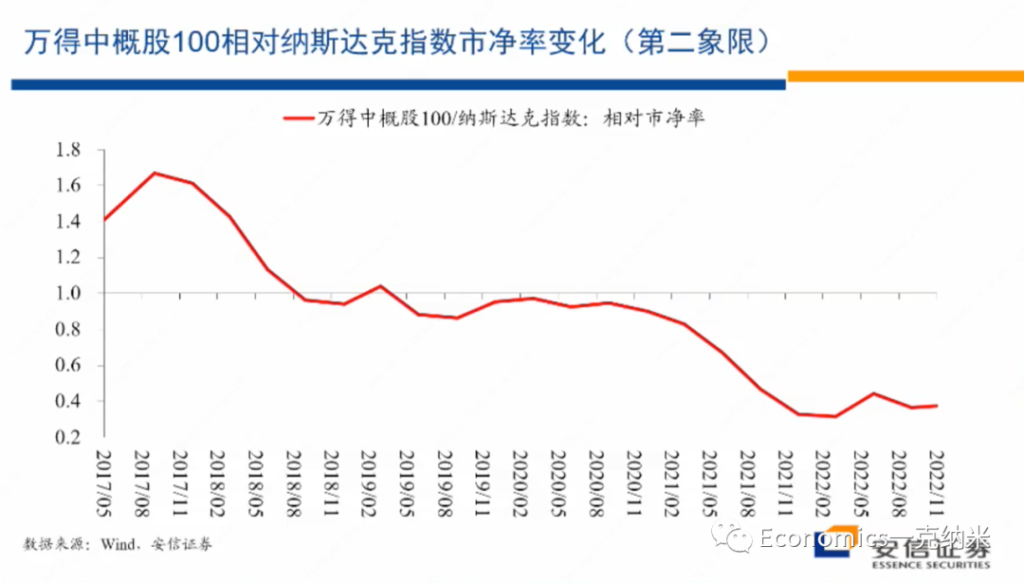
所谓红绿灯体系就是有些领域是红灯,有些领域是绿灯。也许我们还要等一等才能看到,但是红绿灯体系显然意味着对这一行业的话,在未来的话会有更多的限制性的措施。同时在这一领域适当的去引导国有资本的适当的扩大,对这一领域的参与,也是回应政府安全关切的非常重要的维度。
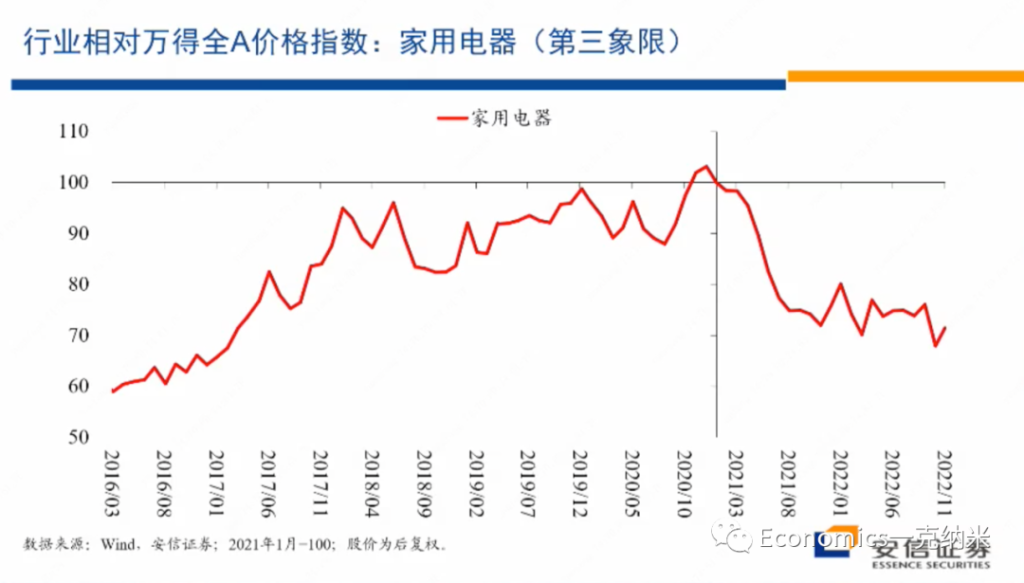
- 第三象限 – 家电
第三象限的例子是家用电器,实际上可以放入第三象限的行业还很多,但是这个需要逐个行业去研究。我们就先拿了家用电器,因为家用电器我们认为比较典型,它不涉及安全关切行业有没有什么增长。
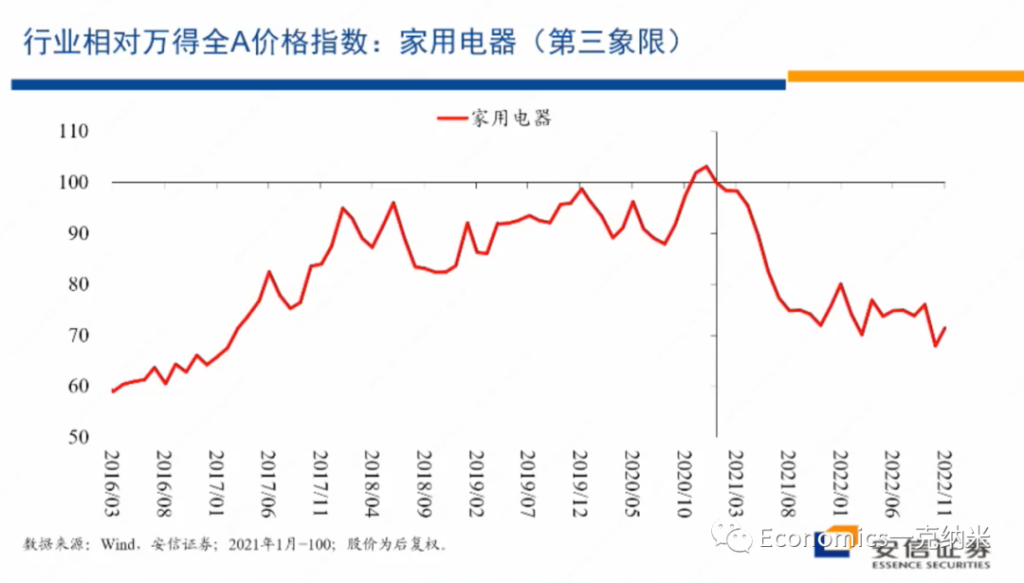
上图是家用电器相对万得全A指数的一个相对价格指数的情况,总体上17年以后有几年的增长,那么21年以后的话,在不长的时间里边把几年的增长吐得差不多了。
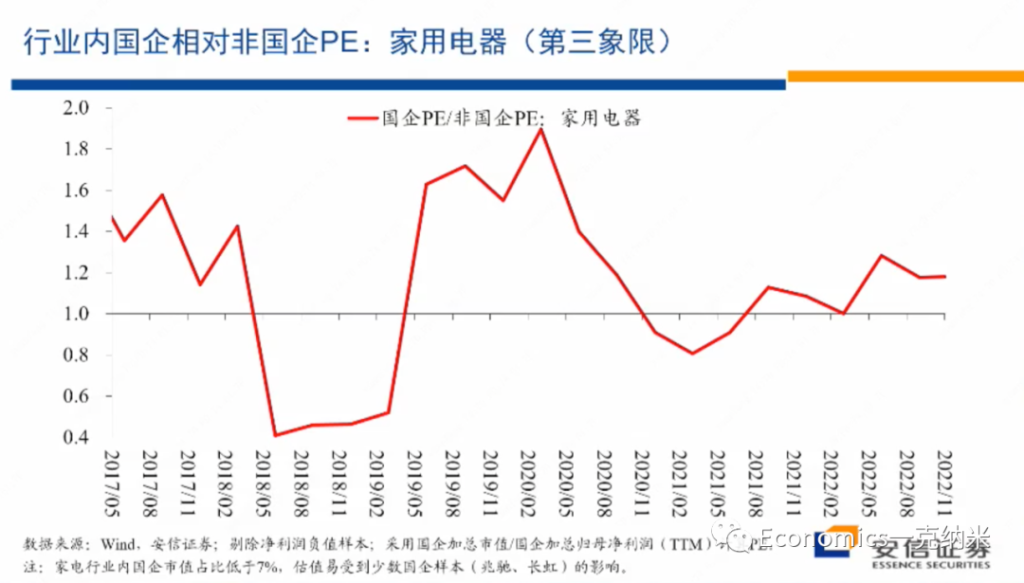
但是我们看这个行业内部国企相对非国企的估值层面的变化,总体上来看,尽管在国防军工领域,我们看到了国企的估值优势相对在扩大,但是在家用电器这个领域,国企相对非国企的相对估值体系总体上是相对比较稳定的。
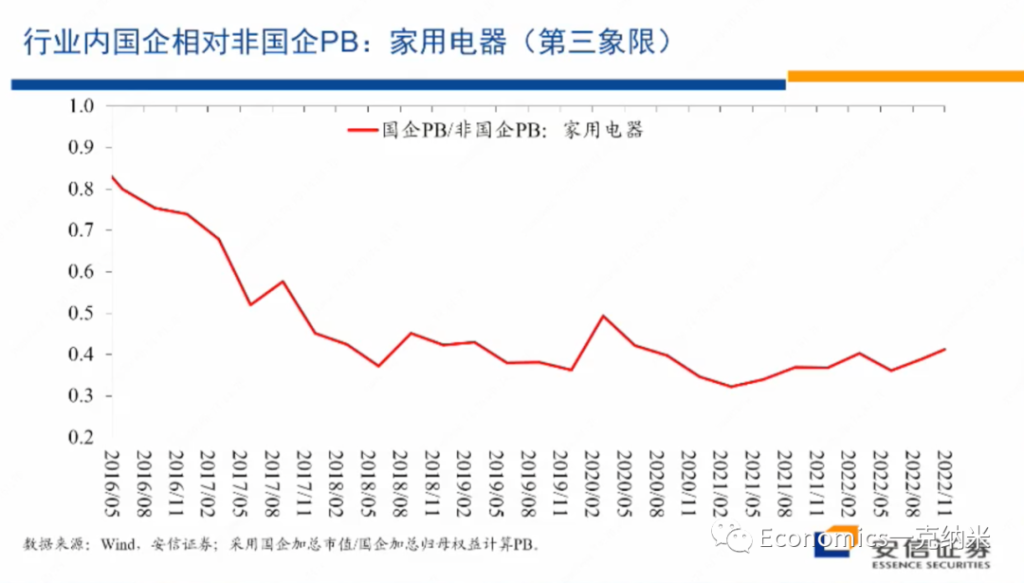
无论是从PE的角度来看,还是从PB的角度来看,相对的估值体系都是比较稳定的。换句话来讲,从市场观察的角度来讲,在这一领域不存在安全关系,不存在反对资本无序扩张,不存在走回头路,不存在国有企业获得了更大的一个政府的扶持或者是政策上的优势,这个行业的经营环境法规环境等等是相对稳定和透明的。
实际上很多的行业也许都处在领域,那么对这个领域来讲,继续去参与全球的分工合作和竞争,毫无疑问的话应该是在政治上在全球规则上应该是没有什么障碍的,而且政府也乐于在这个领域的话去继续推动全球性的贸易合作和竞争。但是国有企业相对非国有企业估值的变化与国防军工的话形成了鲜明的对比,同时如果说国防军工随着这几年安全关切的增强,开始获得相对的收益,那么在家用电器这一相对没有明显增长的领域,在这几年的时间里边,实际上的话还有一些价格上的价格的相对万德全A指数的相对的走输,当然这一走输可能有很多行业层面的原因,我具体不是那么了解,但是毫无疑问这不是一个高增长的行业,它的增长的动量没有增强,这个应该是比较确定的。
- 第四象限 – 电力设备 & 新能源车
那么接下来的话我们讨论的是新能源汽车,我们认为的话它是典型的处在第四象限的行业。它是一个存在着高度不确定性的高增长的行业,同时又需要也有可能制定全球性的规则来管理各国政府的补贴,以及其他的一些产业政策,来在这一领域营造一个全球的公平竞争的环境和体制。
当然除了新能源汽车之外,在民用的领域,我们还可以找到不少其他的高增长的行业,我们以新能源汽车为例来看问题。
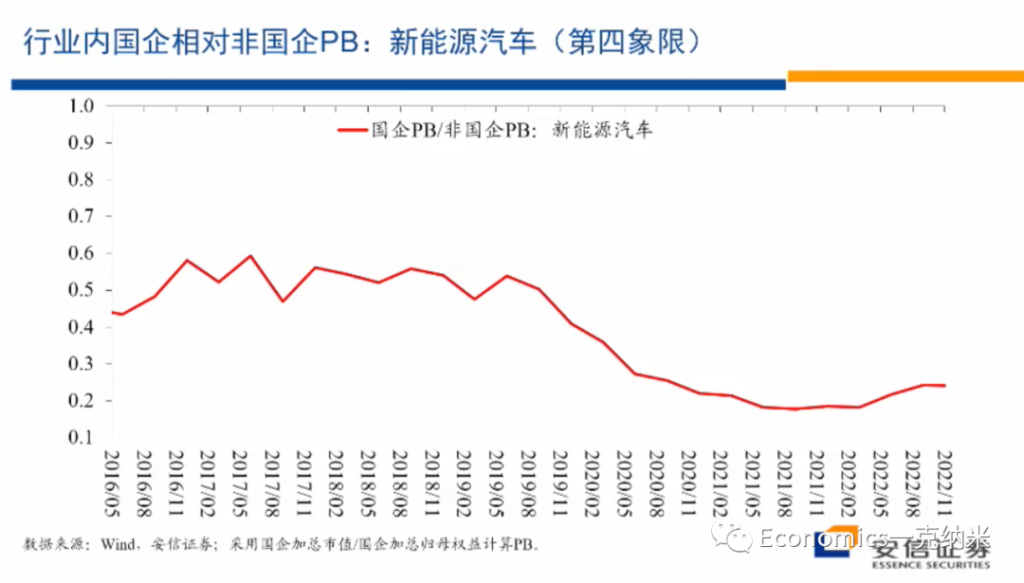
那么毫无疑问,我们知道新能源汽车是一个高增长的行业,进入2020年晚些时候以后,相对万德全A总体上来讲它获得了明显的相对收益。与此同时,在PE层面上,新能源、汽车在2022年5月就是在最近半年以来似乎获得了一些估值的优势,但是在PB层面上这种估值优势是很不明显的。
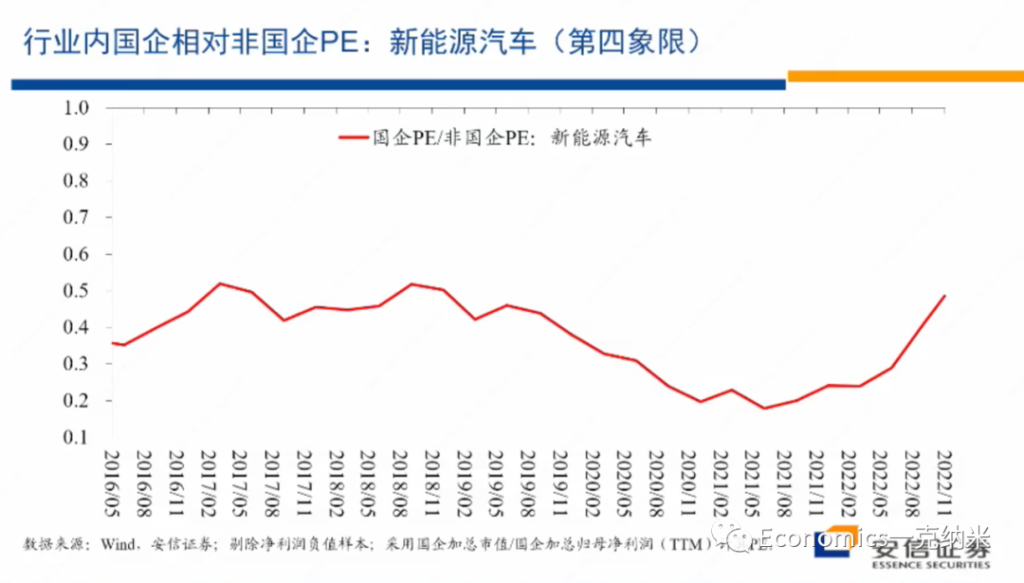
实际上2020年这行业显著的获得相对收益的同时,国有企业的估值的相对的劣势在PB层面上还有一定的扩大,相对于股价的表现而言,相对股价的表现而言,在PB层面上国有企业的估值的劣势的话,相对而言还有一定的扩大。
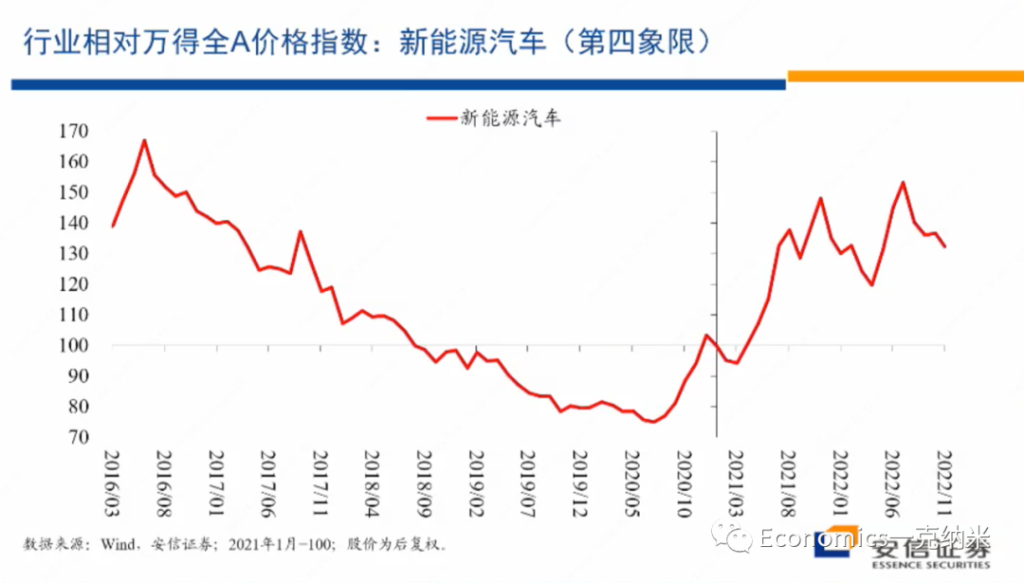
当然未来进一步的变化我们可以继续观察,但是我想说的是迄今为止在新能源汽车上的市场价格的变化,在很大程度上也支持我们一开始在四象限的分析之中,对第四象限的行业特征的定义,就是它继续以民营企业来主导,继续是全球性的继续维持较高的估值。
新能源汽车看起来符合这个定义,而在第三象限的话,整个的竞争环境非常的稳定,然后可以继续坚持全球化,没有任何问题,但是在第四象限的领域,需要强化一些全球性的规则的制定,来维持一个公平竞争的环境,防止安全竞争的过度的波及到太多的行业和领域。
在第一象限的话,我们知道国有企业看起来很可能获得很多的相对的优势,另外的话它是确定的处在一个高增长的领域。第二象限的话面临的主要问题应该就是加强管制红绿灯等等。
最后我们看一个专精特性,在涉及到安全关切的众多的小的细分领域,由于技术上的不确定性,以及这些领域足够的细分,完全由国有企业去主导这些领域,我个人认为可能在操作上不一定那么现实,国有企业也许就是起到主要的骨骼架构的作用,在大量的细分行业里边的龙头,可能主要还有民营企业来主导。那么围绕专精特新的这个板块的话,我们也来看一看它的表现和市场的看法。
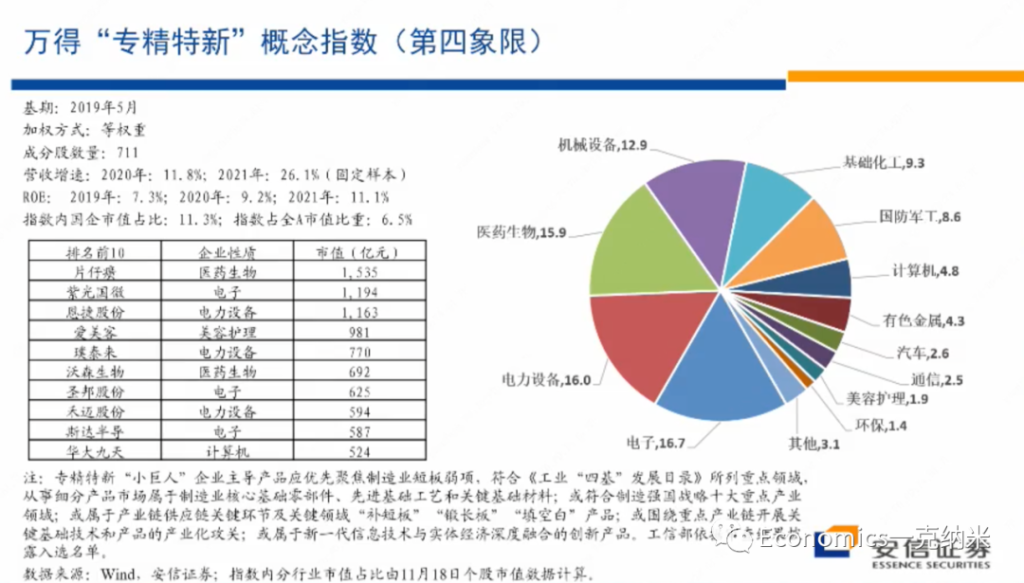
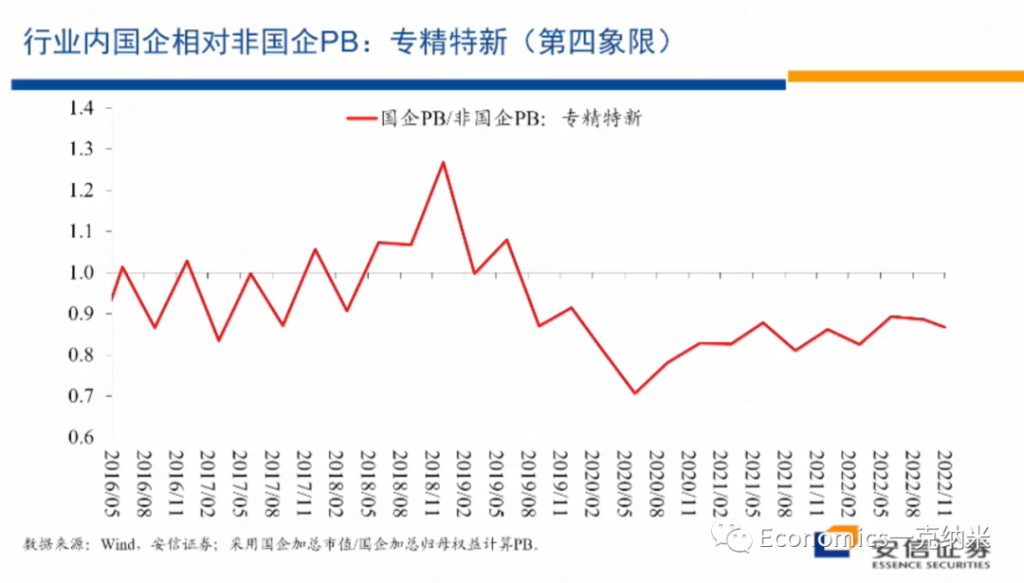
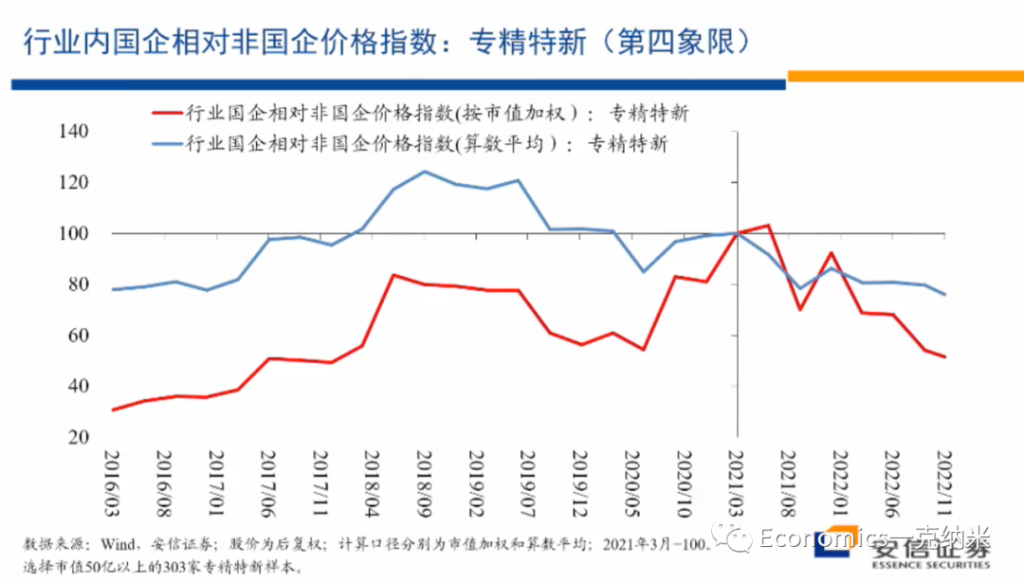
首先专精特新的相对的价格指数,总体上来讲的话,在2021年以来,2020年底以来,相对于万德全A的它有不断扩大的相对的收益。而且在专精特性内部,国企相对非国企的优势,没有特别明显的单边扩大,在PB层面上没有特别明显的单边扩大。在PE层面上,就这几年的情况来看,2020年以来有一些单边扩大,也许与盈利的不平衡有关系,但是在PB层面上,国有企业相对非国有企业的估值优势的单边的扩大是不明显的。

由于这样的原因,我们把专精特新的放到了第四象限,也许有的人的话会觉得专精特新的放在第一象限更合适,但是即使把它放在第一象限,考虑到它涉及到大量的细分行业的龙头,然后在双循环之中是以内循环为主,在细分行业之中主要由民营企业来主导,又是一个高增长的领域,所以它继续会维持相对较高的相对收益。
当然,也许有人觉得专精特新因自主可控等因素涉及安全关切,放在第一象限更合适,这无疑可以讨论。
最后一个部分的话,我们主要是围绕全球性的经济发展环境的变化,想去谈一谈我们的认识,特别是在估值层面上我们的认识。我们想说的是安全与发展并重的关切,不仅对中国重要,对跨国公司对全球很多中央银行,对于一些发达国家来讲都存在这样的倾向。
那么在安全与发展并重的条件下,它与过去效率优先追求增长的就具有显著的差异。那么为了分析这一体系的影响,我们就设了四个象限。那么在四象限的分析体系下,我们会发现对于一些行业它会产生非常大的影响,在一些领域国有企业会获得明显的估值优势。
在另外一些领域法律法规的引入意味着估值体系的重建在另外一些领域的继续去维持和推动全球化,存在这样的可能性,也存在迫切的需要。还有一些领域,过去所发展起来的全球性的经济治理体系,可以继续健康的发挥作用。
那么从估值体系层面上来看,我们四象限的划分在有限的案例之中与市场的估值的相对表现具有一定的一致性,这为我们理解未来安全与发展并重的理念如何落地,它落地必然有一整套的法律法规政策体系。
那么在落地的过程之中,很多的行业都要受到这样或者是那样的影响,然后这些影响在估值层面上将会有什么样的变化呢?可能的话多少会提供一些参照的意义,尽管安全的关键的毫无疑问变得很重要,但是在我们刚才的分析之中,我们也看到在第三象限所体现的全球合作的领域,在第四象限所体现的发展的领域,全球化看起来的话仍然有相当的生命力,那么未来如何会如何演绎的话,让我们拭目以待。
Ref
高善文经济观察
不一样的房地产泡沫 – 高善文经济观察
中国房地产市场
那么我们来看中国的数据,这是中国房地产投资占整个经济比重的一个数据的结果,在这里的话我们剔除了土地购置费,使得房地产开发投资的口径与我们所使用的美国和日本的数据尽量可比。
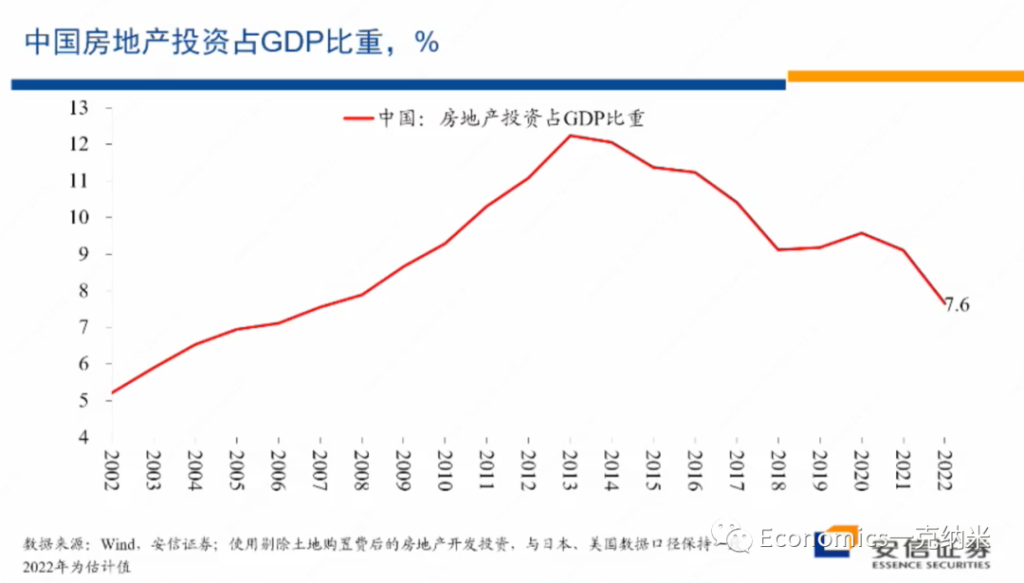
我们看到中国房地产投资占整个经济比重的最高点出现在2013年前,在当时这一比例大概在12%左右,从2014年以后,中国房地产投资占整个GDP的比重,总体上的话就开始经历一个单边的波动下降的过程,到2022年的这一比例估计可能在7.6%左右,7.6%左右的房地产投资占比与日本80年代早期泡沫化之前的水平,与美国2003年之前的水平基本上是接近的,也许略低一些基本上是接近的,考虑到中国的城市化过程还不能说已经结束,考虑到中国的人均收入水平还处在一个相对较快的提升过程之中,城市化过程也还不能说完全已经结束,我们很难认为这样的房地产投资的占比和水平处在明显偏高的状态。
所以从这些数据来看,我们想说的是如果认为2022年我们经历了房地产泡沫的破灭,那么在2022年之前,我们应该看到房地产投资的迅速的放大,迅速的扩大,而泡沫的破灭需要去消化泡沫的扩张过程中所形成的很多的不平衡。但是在房地产投资的数据上,实际上的话在总量数据上,我们并没有看到在2021年之前房地产投资有异常的扩大。恰恰相反,他经历了持续时间的话,也大概有七八年的一个单边的波动下降的过程,而且的话它的绝对的水平考虑到中国城市化的进度的话,也不能说处在异常高的水平。
我们刚才已经看到从我们所使用的估计数据上来看,与投资的数据相一致,中国房地产的一个存货的最高峰出现在2013年前后,当时的投资也处在最高水平。2021年20年前后的话,整个的存货都处在相对偏低的水平。
换句话来讲,也许我们可以认为2019年以来,中国房地产投资的占比基本处在大体合理的水平附近,很难认为市场上积累了非常严重的从总量数据上来看,很难认为市场上积累了严重的供应过剩。
- Key Takeaway:
- 由房地产投资占GDP比例来看,比较纵向过去时间,及横向US&JP,中国房地产市场并未供应过剩。
我们还可以从另外一个角度的话来观察同样的数据,那么在这个数据上的话,我们计算的是房屋的价格弹性,新房的价格弹性。什么叫新房的价格弹性?我们知道在过去十四五年的时间里边,房地产市场经历了好几轮周期,经历了五轮周期。我们计算和比较了梅龙的房地产的下降过程,我们计算和比较了每一轮的房地产市场的下降过程,所谓的价格弹性是这样来计算的。
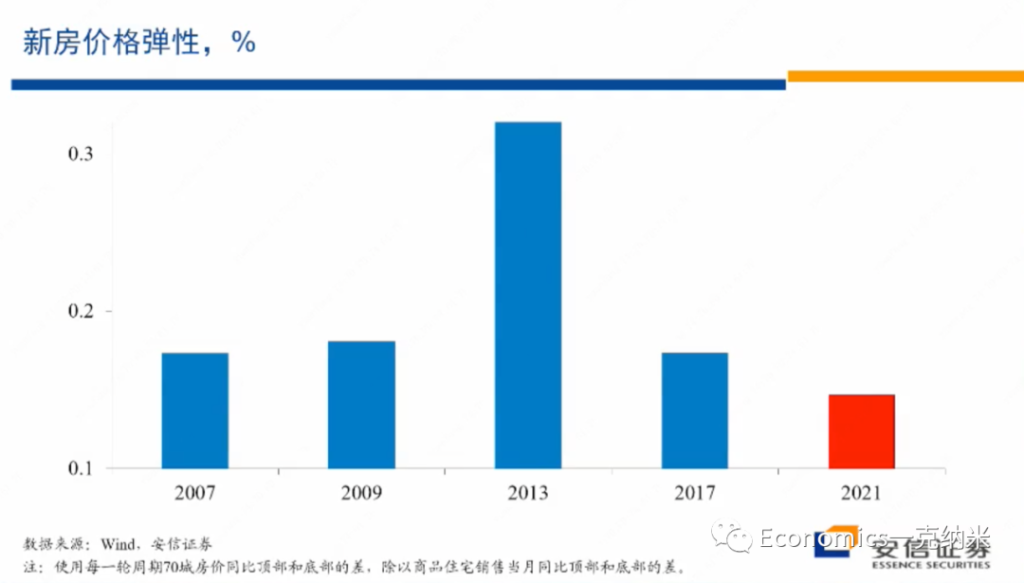
$$\epsilon = \frac{\Delta (每一轮周期70城房价格 P) 顶部 – 底部}{\Delta (商品房销售量 Q) 顶部 – 底部}$$
该比例小,说明他的倒数大 =\frac{\Delta Q}{\Delta P}。价格变化会量变化的影响。
首先我们来计算在房地产市场的下降过程之中,从顶部到底部交易量的下降,我们同时计算从顶部到底部新房价格的下降,然后我们把价格的下降与交易量的下降,计算一个比值,计算一个百分比的比值就得到一个弹性。
那么这些弹性我们认为它的含义在哪里?我们认为这一弹性的含义就像我们在这里所能看到的一样,我们已经知道2013年房地产投资占GDP的比重是最高的,我们所估算的房地产的存货也是最多的,但是2013年在价格下跌过程之中,这一弹性也是最大的。
价格的弹性,在一定程度上代表了市场的供应压力,代表了供应曲线的斜率,代表了市场上的供应压力。在2013年,我们知道各方面的供应压力都是最大的,但是在2013年的时候,新房的向下的价格弹性也是最大的。
以此来对比,在2021年以来的这轮房地产价格的下跌过程之中,尽管交易量的下跌是比较惊人的,交易量的下跌我刚才讲有疫情所带来的影响,疫情的话使得大家带来了很多心理的疤痕,也有的话房地产市场自身调整的影响,所以房地产市场的一个交易量的下降是很大的。
但是从弹性的角度来看,在2021年以来的这一轮房地产市场调整过程之中,它的弹性是过去15年之中最小的。现在的弹性比2017年小,比2009年小,比2007年内容的话也要更小。在价格层面上更小的弹性,我们认为也支持这种看法,就是市场上的供应过剩的压力,至少在新房市场上并不可能显著,市场上没有显著的供应过剩的压力,显示它与一般的房地产泡沫破灭相比,具有一些显著不一样的特征。
我们可以继续计算在二手房市场上的价格弹性,那么相对比较一样的特征是2013年在新房市场上有巨大的价格压力,价格弹性很大,在二手房市场上,2013年的时候,价格压力也很大,价格弹性也很大。
但是从弹性的角度来看,在2021年以来的这一轮房地产市场调整过程之中,它的弹性是过去15年之中最小的。现在的弹性比2017年小,比2009年小,比2007年内容的话也要更小。在价格层面上更小的弹性,我们认为也支持这种看法,就是市场上的供应过剩的压力,至少在新房市场上并不可能显著,市场上没有显著的供应过剩的压力,显示它与一般的房地产泡沫破灭相比,具有一些显著不一样的特征。
我们可以继续计算在二手房市场上的价格弹性,那么相对比较一样的特征是2013年在新房市场上有巨大的价格压力,价格弹性很大,在二手房市场上,2013年的时候,价格压力也很大,价格弹性也很大。
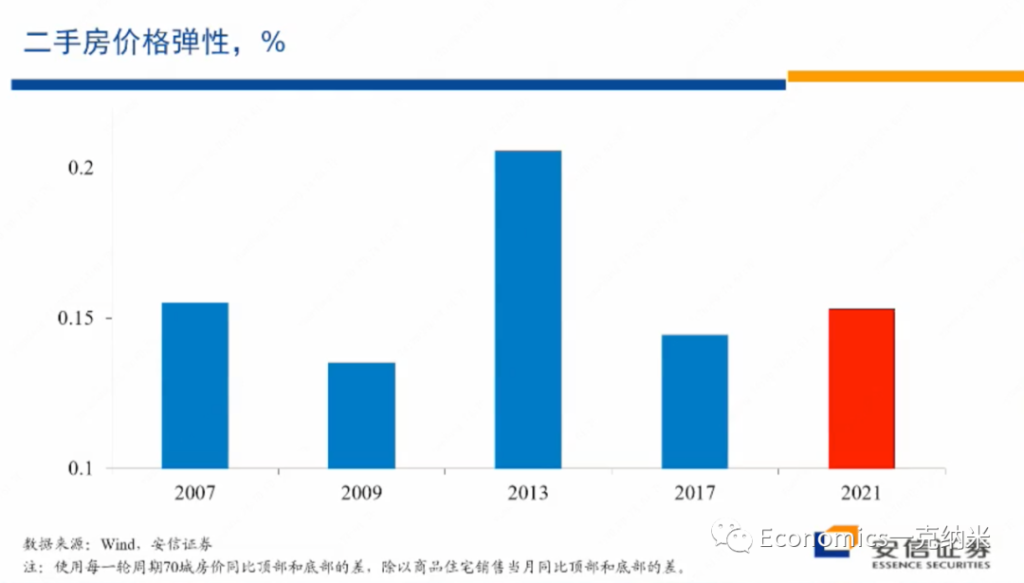
那么从二手房市场的价格弹性相比,今年以来的价格下跌的压力要更大一些,但是显著的低于2013年的水平,也许接近或者是略低于2007年的水平,比2017年的水平略高一些。换句话来讲,看起来新房市场的所承受的价格压力,供应压力比新房比二手房市场相对于新房市场的话看起来要略大一些。
一个额外的解释的话,也许是一部分的住户面对疫情,对于生意对资产负债表所带来的冲击,就像减持股票一样,被迫减持多余的房地产,从而在房地产市场上,除了相对新化市场造成了一些额外的压力,但是这些压力相对2013年相比并不突出,跟2007年的水平相比,也许差不多,放在历史上来看的话,也许就处在中位数附近的水平。
结论
那么做完这些比较,我们想做的结论是什么?尽管不少舆论认为2022年中国经历了房地产泡沫的破灭,这一破灭的话,对未来几年的经济增长都会形成持续的负面影响。但是我们从这些数据想得到的结论是,2022年中国房地产市场经历的应该不是一次泡沫的破灭,至少它不是一次典型的泡沫的破灭。
实际上的话我们倾向于认为房地产市场2022年的房地产市场经受了两个因素的打击,而不是一个泡沫的破灭。
一个因素的话就是持续的疫情形成了疤痕效应,疤痕效应使得住户不敢买房,同时还在一定程度上去减持房地产市场的持有,在需求端造成了压力。
另外一方面,在2016年以后,房地产行业逐步开始流行所谓的高周转模式,高周转模式作为一种商业模式,具有巨大的内在脆弱性。高中的模式对于本质上是一种高杠杆模式,对于连续的融资,对于顺畅的融资,对债务工具的依赖非常的强烈。
所以但是由于这样或者是那样的原因,在2016年以后,房地产行业开始流行高周转模式,高周转的模式作为一种商业模式,具有巨大的内在脆弱性,那么高周转模式的内在脆弱性,由于房地产调控等原因的话被充分的暴露出来,迫使整个行业需要转变,自己的商业模式需要大幅度的修正。
而房地产行业在修正、在放弃高周转模式的过程之中,又遭遇了疫情的疤痕效应,在需求端所造成的冲击。
在这两种因素的条件下的话,我们我们认为的话在很大程度上回应了2022的话,房地产行业的状态销售非常的低,然后开工非常的低,投资大幅度的下降,然后全行业的话面临着相当普遍的不断蔓延的,在前一段时间以前比较普遍的不断蔓延的一个违约的压力。所以我们认为它不是一个由供应的过剩所推动的典型的房地产泡沫和泡沫的破灭,而是一个房地产行业经历了由于高周转的模式的内在脆弱性所带来的流动性危机。
这些流动性危机由于疤痕效应在房地产市场上的影响进一步加剧,那么我们看到最近一段时间以来的话,政府对房地产行业采取了非常强有力的一个扶持政策,对于一些大型的头部房企来讲,流动性压力出现了一些明显的缓解。
但是就像我们第一部分曾经讨论的那样,疤痕的消退,财务的疤痕、心理的疤痕、疤痕的消退需要时间,意味着在需求端的房地产市场的需求的恢复需要较长时间,不会很快就出现微型的反弹。政府看起来也没有刺激房地产需求的愿望,在政治上的这种做法也很难受到欢迎,同时疤痕效应的持续存在,也使得民众很难迅速的去增加房地产市场的风险暴露。另外从高周转模式转换到更可持续的制造模式,也是需要较长时间。
尽管流动性危机在行业层面上正在经历明显的缓解,头部企业的流动性的状况有明显的改善,但是房地产行业从高周转模式,顺利的转换到实际上我个人认为是制造模式,也需要较长的时间,这意味着的话我们现在所看到的政策以及市场的调整,意味着房地产行业转入了一个有序的供应端的出清,房地产行业正在转入一个有序的供应端的出清,但是行业迅速经历需求的强劲和持续的恢复,房地产投资迅速经历非常强劲的上升,房地产新的商业模式迅速到位,可能在短期之内都不是特别的现实。
看得更长一些,我们这部分讨论的话所面临的比较大的问题是,由于房地产行业正在经历一个有序的供应端的出清,由于过去几年新开工,总体上处在相当低的水平,从宏观上的房地产投资占比,以及我们所估算的行业的存货压力来看,即使在现在房地产行业的意愿存货水平都处在偏低的水平,但是这一偏低的状态在未来无疑的话会继续维持,甚至会进一步强化。那么这些因素合并的结果是在较为长期的将来,房地产疤痕效应消除,房地产行业的商业模式转换完成以后,在市场的需求开始正常化以后,在一段时间里边也许会面临着市场供应不足的压力,而市场供应不足的压力在很多层面上,包括对房价等等的都会产生一定的不利的影响。
如果我们回顾2016年的三去一降一补之中的去产能,对很多的产能过剩行业所采取的强有力的去产能措施,我们就会知道当时的去产能措施在一段时间以后的话,都产生了这些行业价格非常强有力的上升。而且这些上升事后被证明的话是可维持的,因为很多被去除的供应再也没法回来了,相对去适应一个供求偏紧的局面,很多行业的产品价格经历了很大的上升,它的一个价格波动的中枢都上升到相对以前的更高一点的水平。
那么在中国的房地产市场来讲,我们刚才讲现在的房地产市场在过去几年并没有经历供应过剩的积累,相反从很多的数据上来看,供应是偏少的,但是在现在的市场条件下,无论是民众的疤痕效应,还是房地产企业的一个创业模式的调整,都意味着这个市场仍然处在一个相对非常弱的状态。但是这个市场未来总会正常化的,疤痕效应加以较长的时间总会消除的,然后房地产市场供给侧的出清也会逐步有序的完成,然后在那个时候房地产市场会是什么样的状态,也许站在现在我们都要提前的有所考虑。
- Key Takeaway:
- 1. 从 房地产投资占GDP的比重看,中国房地产并严重供给过于需求。
- 2. 从 新房和二手房弹性看,可以得出类似的结果,供给可能并没有远高于需求。基于以上,房地产市场可能并不存在泡沫。
- 3. 但是基于 二手房弹性的数据看,疫情的确给households的资产负债表带来重创。一个假设是:asset price decrease, but debts keep the same。于是households必须要卖房以补充equity。因此,疤痕效应随之而来。
- 4. 2022年房地产市场衰落可能并不是因为泡沫。而是一下可能的两个原因:1. 疤痕效应。2. 房地产企业高周转的经营模式及其脆弱,在疫情带来需求减少且违约增加的情况下崩溃。房地产低迷是因为模式脆弱导致的流动性危机,而不是供给过剩带来的泡沫破灭。
- 5. 房地产行业因此需要经历一个 由高周转模式 – 生产制造模式的调整,需要很长时间。且疤痕效应消退需要很长时间。但是,当以上问题被消化的过程结束时,可能会有供给小于需求。(类比2016年三去一降一补,去产能的过程)。
Ref
高善文经济观察
疫情留下的疤痕 – 高善文经济观察
- 1. 疫情留下的疤痕
- 2. 不一样的房地产泡沫
- 3. 安全与发展:估值结构变化
疫情留下的疤痕
回顾这三年的疫情,应该说给经济和社会生活留下了很多的伤疤,有一些疤痕或者是伤疤,主要是在住户部门在很多的企业的资产负债表上,主要的问题是在过去几年,经济活动都不能够正常的展开,收入的不稳定性,空前的大收入的增速跟疫情之前相比,总体上也经历了比较明显的下降,在这样的条件下,住户和不少企业的资产负债表受到了不小的损害,权益科目出现了一定的问题,而这样的问题毫无疑问正在并且在未来需要花一些时间去进行修复。
疫情给一般民众的心理也多少留下了一些伤疤或者是一些疤痕,大家对于风险的容忍和承受能力相对于疫情之前相比可能出现了一定的下降。大家对未来收入的增长的确定性可得性以及未来收入增长能够维持在什么样的水平?
存贷差 代表着households对收入的预期
在这些层面上大家的预期呢也都变得更加保守,而这样的心理上的疤痕也影响了住户和企业的很多的经济行为,就像我们在这张图上可以清楚的看到的一样。
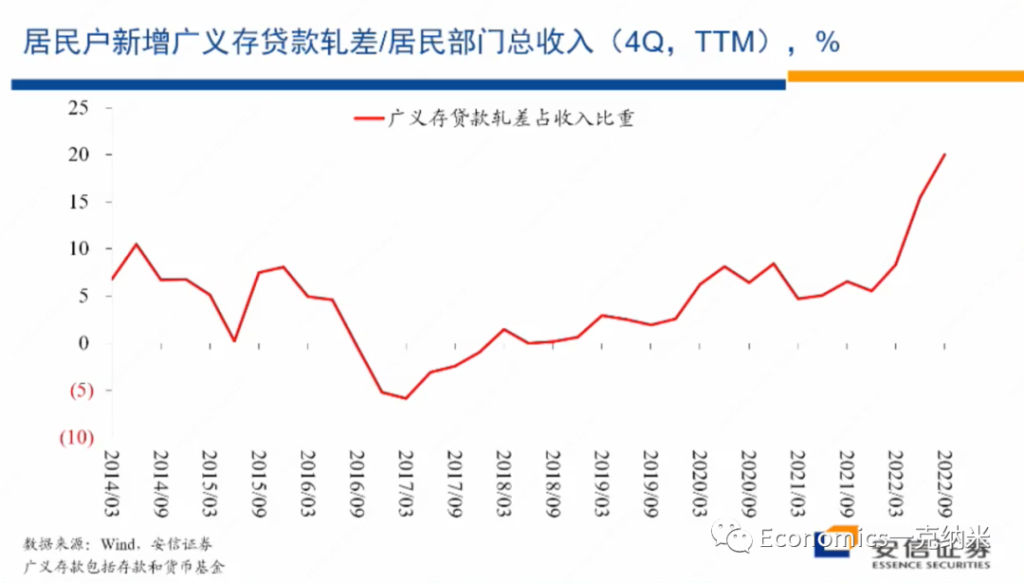
在这张图上在分母上,我们放的是居民部门的一段时间的收入水平,比如说一个居民户,然后在这个季度他有多少收入,在分子上我们放的是在居民户的资产负债表上,它存款的增量减去贷款的增量,居民户部门有一些收入,这些收入有一些当然用于消费了,但是也有一些的话多多少少的话通过货币基金,通过银行存款的都存储起来了。
$$ \frac{ \Delta (存款 – 贷款) }{一段时间内的收入_{存量}} $$
相当于 净贷款, Net Saving, 占收入的比例。存款科目上包括了它的储蓄存款,也包括了购买的货币基金,然后再扣减掉居民户出于购买房地产以及经营需要的话所获得的贷款。 ratio的 数值越大,相当于:净存款占一定期间收入的比例增大。如果净存款增加代表居民对安全的需求增加,那么此ratio说明了,在2022年居民对安全的需求急剧上升。
我们可以清楚地看到,在今年的3月份以来,相对于居民的收入而言,居民户所持有的存贷款或者轧差结束以后的存贷款的占比出现了幅度非常大的上升。即使在2021年年底的时候,这一比例在过去七八年的时间里边相对已经处在较高水平。但是进入2022年以来,这一比例在那样的水平上继续出现了单边的历史上少见的幅度非常大的上升。那么这样的资产负债表调整的变化显示了总体上来讲,居民户部门在资产配置上变得非常的保守,不愿意承担风险,对未来的预期的话变得更加悲观。
储蓄率,代表着households对收入的分配 Y – T = C + S; S = sY
那么我们再看第二个数据的话,是对居民户部门储蓄倾向的观察。所谓的储蓄倾向就是一段时间的一段时间里边,居民户的话获得了一定的收入,这些收入之中的一部分用于消费,比如说购买食品、购买烟酒、购买汽车等等一部分用于消费,那么把居民户的收入扣减掉它的消费以后,它的剩余项一般在经济学上定义为它的储蓄,所以它的储蓄可以是居民户所进行的投资,也可以是进行的房地产购买等等。
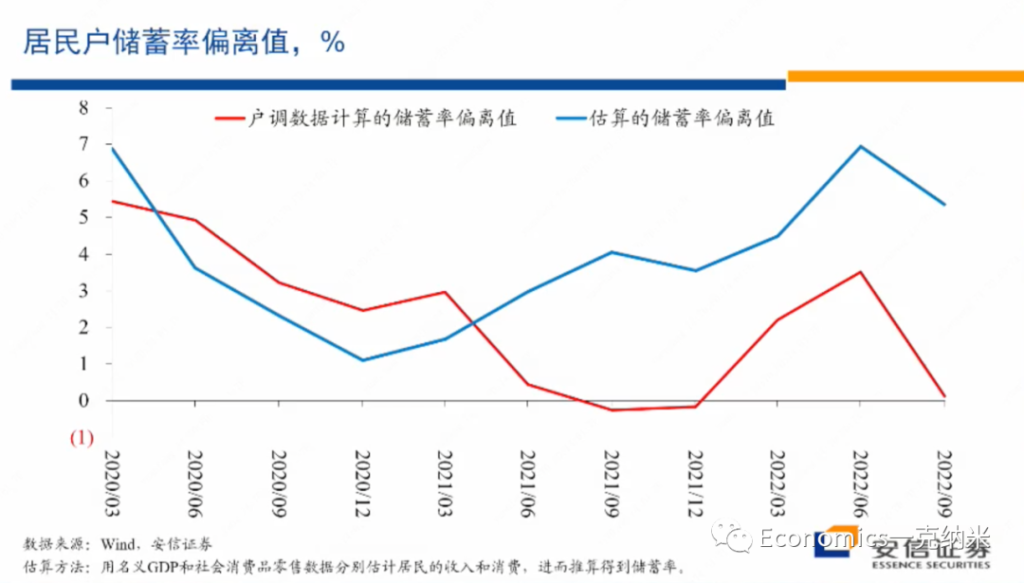
那么在这样的定义下,我们来观察居民户部门的储蓄率的变化。在这里我们这个报告了两个数据,红色的线使用的是入户调查数据,在入户调查数据之中,我们看到的情况是每一次比较明显的疫情冲击,都导致居民户部门的储蓄率有异常的上升。
这样的上升 一部分是因为部分的线下消费活动不可得,形成了被动的储蓄,另外一部分也可能来源于大家对未来收入的稳定性和可能性的信心下降,在这样的条件下,它需要有更多的储蓄。但是上面的蓝色的线是我们基于宏观的数据,基于宏观的国民收入,基于宏观的消费数据所反推出来的居民户部门的储蓄率。我们看到这两个数据有一定的差别,特别是在疫情以来,它们的走势的方向以及的水平应该说差别比较大,甚至是越来越大。
如果我们以宏观的数据估计为基础,总体上我们看到的是在趋势上居民户部门的储蓄率不断的上升,居民户部门的消费倾向是越来越低,他同样的收入它越来越多的用于储蓄,而不是用于消费。同时对储蓄起来的这些收入而言,更多的是放在存款、货币基金等高度稳定的科目上。用于购买房子,用于比如说持有权益资产等等的,从其他的一些数据来看,都经历了单边的大幅度的下降。
所以我们刚才所报告的这两个方面的数据,一个方面是居民户部门储蓄率的变化,另外一个的话是居民户部门资产负债表上金融科目存贷款科目的变化,这两个方面的数据清晰的向我们展示了几年的疫情,给居民户部门带来了比较明显的伤疤,这些伤疤有一些是心理性的,影响了对未来的预期。有一些的话是资产负债表的,是财务性的,特别是伤疤效应,在2022年以来有比较明显的上升,这些伤疤效应在这张图上有比较明显的上升。
而至于下跌的同时,在宏观上并没有出现明显的通货膨胀,明显的监管的收紧,明显的流动性的紧缩,明显的货币信贷利率的显著的上升,这些因素都没有。但是的话总体上权益市场包括房地产市场都出现了单边的幅度比较大的调整,而且在2022年的调整幅度异常大。那么由于三年的疫情所带来的疤痕效应,我们想说的是看起来即使在社会经济生活逐步恢复正常以后,疤痕的修复它的影响完全消除,可能也是需要一些时间的。
由于三年疫情,对于普通民众在财务上所造成的很多的伤害,那么为了重建资产负债表,为了重建它的权益科目,这个都是继续需要一定的时间来积累储蓄去进行修复的,普通的民众对未来的收入的增长重新建立更强的信心,在这样的条件下去逐步的降低自己的储蓄倾向,并且的话愿意持有更多的风险资产,而这样的心理的修复也是需要时间的。
- Key Takeaways:
- 存贷差增加,体现出 households 预期 Y下降
- Saving Rate增加,体现 households对consumption需求下降,savings增加。
- 因此,consumptions因以上双重原因叠加,下降。
- 也因此,预期未来的增长,下降(预期变化是最重要的acyclical factor)
- 疤痕 消失 需要时间
A CASE STUDY
那么从文献上对于自然灾害等因素,对于人类心理的影响来看,一般认为在人类经历了自然灾害以后,在心理上都会产生一些疤痕,这种疤痕在自然灾害消失以后的话会维持一段时间,尽管的话随着时间的流逝,它的影响在减弱,但是会维持一段时间,而且它突出的特点是对风险的容忍度在下降,他的行为的话变得更加保守,更加不愿意冒险,但是的话对这样的一般性的总结看起来似乎也有一些例外。
比如说2002年的时候,在德国的易北河岸发生了一次严重的洪水,洪水过去以后,一些学者就专门调查了受到洪水影响的居民的收入和开支行为。
那么基于可得的地理数据,在发生洪水的时候,在同样一个地理区域,并不是所有的家庭都受灾了。有一部分家庭受灾了,有一部分家庭没有受灾,这样的话在同样的地理区域,没有受灾的家庭的收入和开支行为,就可以作为一个很好的对照样本,去对比和研究受灾以后受到洪水冲击影响的家庭在洪水过去以后,他们的收入和开支行为。那么对于这样的一个样本的研究,显示在易北河洪水以后,实际上受到洪水影响的这部分家庭的收入和开支行为并没有受到明显的影响。
这个与我们一般想象的疤痕效应应该说存在存在一定的差异,但是这些学者倾向性的解释是德国有强大的社会保障体系,所以在这些地区发生洪水以后,这些民众所遭受到的损失由政府及时和足额的提供了补偿。
那么由于这样的政策干预,无论是在财务上还是在心理上,都没有在民众的生活之中留下明显的影响,他们的生活在洪水过去以后就迅速恢复正常。政策干预,相当于给household在预期及实际上都给予了补助。
在一定程度上,如果我们观察今年美国的储蓄率的变化,美国普通的住户部门储蓄率的变化。尽管美国也经历了非常大的疫情,但是今年以来的话,在美国住户部门的储蓄率的变动上,也看不到非常明显的疤痕效应。如果有很明显的疤痕效应,至少相对疫情之前相比,它的储蓄率应该更高。但是在我们所看到的数据之中,似乎在美国的住户部门,它的一个这个储蓄率相对于疫情之前可能还要更低一些,看不到明显的疤痕效应。而这样一个相对更低的saving rate,在一定程度上与美国经济数据的强劲以及通货膨胀压力之间的可能也是有一些关系的。
那么从易北河洪水的案例的研究来看,一个可能的原因也是在疫情肆虐的时候,美国政府针对住户提供的大量的补贴和转移支付,很好的保护了住户部门的财务状况,很好的保护了住户部门的心理上所受到的冲击,所以在疫情结束以后,他们的生活就迅速回到相对比较正常的状态。US Case,与德国洪水Case的政府政策弥补似乎得到一致的结果,政策支持帮助缓解疤痕。
但是从中国迄今为止的数据,以及从比较多数的对自然灾害条件下,人们行为的变化的研究来看,我们认为有理由相信在我们的经济社会生活逐步恢复正常以后,疤痕效应相对还会持续一段时间。也许的话随着时间的流逝,它会逐步的减退,随着疤痕效应的逐步的减退,储蓄倾向的逐步的下降,居民户部门逐步的相对变得更加愿意接受风险。这些变化在别的因素都不变的条件下,可能为权益市场也许还包括房地产市场提供了一个更稳定更强劲和更持续的基础。
- Key Takeaway
- 1. 疫情带来的疤痕效应,会在长期减少households对收入和消费倾向的预期。
- 2. 疤痕效应在没有足够政策支持的情况下,会持续很长时间。
不一样的房地产泡沫
那么下来在第二个部分,我想跟大家分享一下我们对中国房地产市场泡沫的看法。2022年的中国房地产市场经历了幅度很大的调整,销售和新开工的下降幅度十分惊人,房价也出现了一定的下跌,房地产行业出现了非常广泛的违约压力。
很多人认为中国正在经历房地产泡沫的破灭,一些悲观的看法,基于对日本房地产泡沫破灭的观察,包括对于美国房地产泡沫破灭的观察,认为泡沫的破灭在一定程度上是不可逆的,并且它将会在未来较长时间里对于经济增长形成比较长期的负面影响。
我们知道日本的泡沫破灭以后经历了失去的10年20年,美国的房地产泡沫破灭以后,经济至少也经历了差不多5年时间的非常弱的增长。所以确实有不少人认为中国的话在2022年正在经历一个房地产泡沫的破灭,而这一破灭过程是不可逆的,并且将对未来几年的经济增长投下长长的阴影,我个人认为的话这样的看法不尽合适。
中国房地产容纳了too much wealth. If bubble collapses, both the market and the credibility sucks. Local Gov starts to stop people building houses in the rural area, which is equivalent to the gov enforces people buy rubbish apartments in ‘cities’, to stimulate demands and fill the financial gap for real estate firms. Extracting households’ wealth to save the financial burdens for firms and gov continues.
以下高善文从存货的角度分析了房地产市场的供求
接下来的话我来谈一谈我个人的话针对房地产市场的看法。首先我们跟大家分享一下我们这些年以来所追踪和估算的一个数据,这个数据的话是叫做在房地产行业之中所持有的非意愿的存货,非意愿的存货。所以的话它在0这一水平不是意味着存货是0,而是意味着房地产企业的存货与房地产企业意愿持有的水平是一致的。
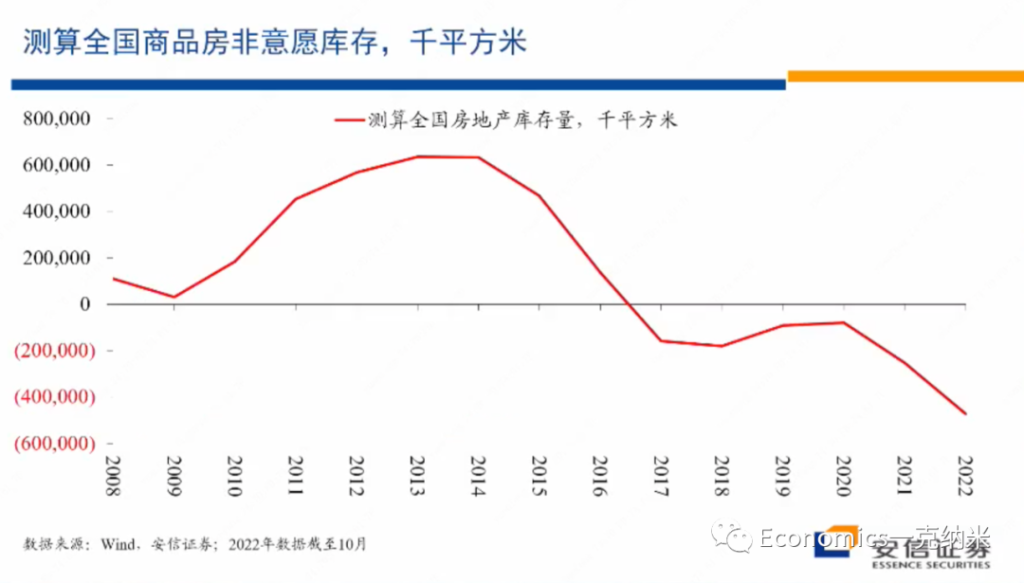
那么从这一估计结果来看,毫无疑问在13、14年前后,房地产行业曾经积累了大量的超额的存货,但是在2018年以后,这一存货水平基本上就已经下降到完全正常的水平。从这一估计来看,2021年和2022年房地产行业所持有的非意愿的存货放在历史上来看都处在异常低的水平,它的非意愿存货放在历史上来看,都处在非常低的水平。
这些数据估计的意义在哪里?我们再来看。我们知道的话,所谓的房地产泡沫,它的形成通常有几个条件,第一个条件的话就是大量的民众和金融机构对未来至少是对房地产行业的未来抱有强烈、不可动摇的信心和信念,认为房价一直会涨,对房价和房地产市场抱有不可动摇的非常强烈的这个信念。
第二个的话就是整个的金融条件和金融环境异常的宽松,所以当他们试图去参与房地产市场的投机的时候,总是可以以比较低的资金成本获得贷款,在这样的条件下的话,大家都对房价具有很强的预期,又很容易获得贷款。这些因素合并在一起的话,推动了房地产泡沫的形成和房价的快速上升,房价的快速上升会刺激房地产供应的扩大。因为大家都觉得这个房子好,房价要涨,所以都来买房价就在涨。
那么面对房价的上涨,供应商房地产开发商的话,就能够和愿意在市场上提供更多的住房,在这样的条件下,房地产市场的供应的话就会大量增长。但是等到房地产泡沫破灭的时候,就会发生两个方面的问题,一个方面的问题是在泡沫化的过程之中,房地产市场有大量的异常的过剩的供应,就是在泡沫化的过程之中,房地产市场的经历的供应的扩大,从长期历史来看的话是不正常的,那么这些过剩的供应,这些不正常的供应,需要时间的来消除,需要时间来消化。为了消除和消化这些不正常的供应,就会对房地产的投资,对很多的相关行业的需求形成时间非常长的负面的影响。
那么第二个问题,就是在消化这些过程供应的过程之中,由于市场上在泡沫破灭以后存在明显的供过于求的现象,那么在泡沫破灭以后的话,房地产价格会经历下跌。房地产价格的下跌对银行的资产负债表,对住户的资产负债表形成了很大的损害,这些损害迫使银行回头要去修复自己的资产负债表,要去紧缩信贷,提高信贷发放的标准,要去筹集资本,甚至的话要去隐藏坏账,来修复自己的资产负债表。
而对于住户来讲,在投机性的购买过程之中所积累的房地产的持有,在房价下跌的过程之中,由于它同时持有大量的银行的债务,在这样的过程之中,它的住户部门的资产负债表就会受到很大的损害,而住户部门资产负债表受到的损害,在泡沫破裂的过程之中,也是需要花很长时间来修复的。加杠杆投资房地产时,QT带来资产价格下砸,asset price going down, but debts keep the same,=> 资产负债表恶化,equity缩水。
我们刚才所讨论的这些泡沫形成和破灭过程之中,所重点想强调的是一个严重的造成持续影响的房地产泡沫,一定有一个关键的特征,就是从宏观上来看,房地产投资的异常扩大,即便是在整个房地产行业里边没有持有过剩的存货,但是从宏观和总量上来看,一定有房地产投资的异常扩大,房地产投资的异常扩大,显示了房地产市场供应的扩大。
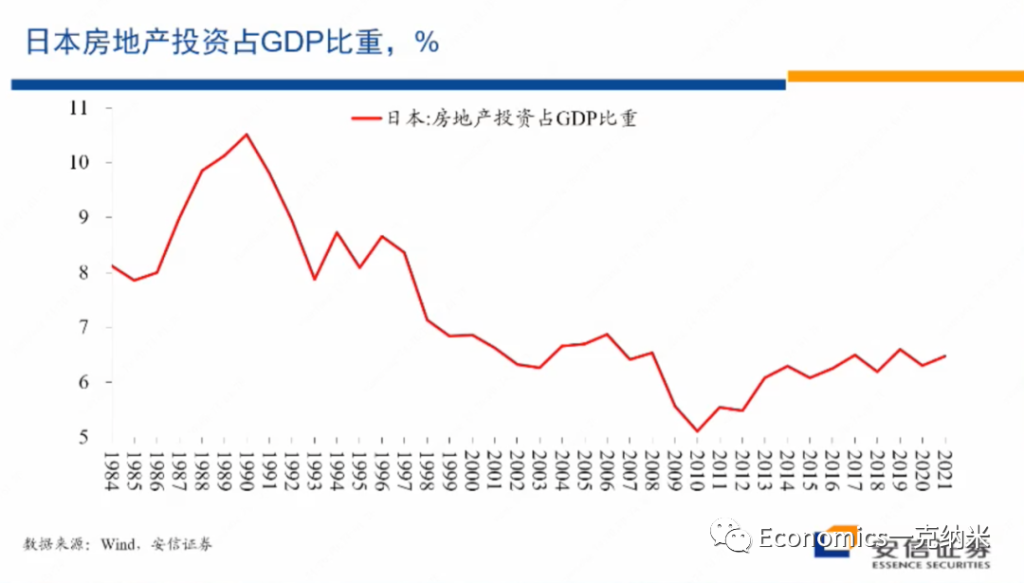
随后在房地产泡沫破灭的过程之中,又经历了房地产投资的下跌,房地产投资的下跌毫无疑问对经济活动形成打击。房地产投资的下跌伴随的是房价泡沫的破灭,对银行和住户的资产负债表,甚至包括企业的资产负债表又形成很大的损害。那么我们用这样的模式来看,日本的房地产,日本在1985年之前,房地产投资占整个经济的比重大约在8%左右,在87年房地产市场开始泡沫化以后,这一比例迅速的从8%的上升到超过10%的水平,上升了超过10%的水平。而这些过程显示了在市场上房地产供应的扩大。
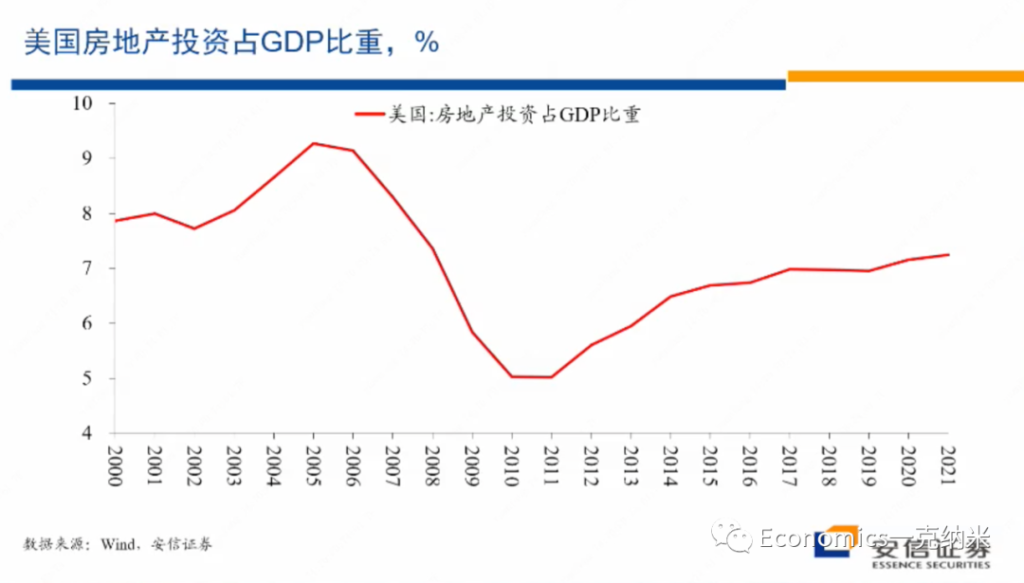
而1991年房地产泡沫破灭以后,日本的房地产投资就开始经历了一个长期的下跌过程。至于下跌过程的早期,可能主要反映的是对于过剩供应的消除过程,而这一投资占比下降的后期的变化,也许更多的与日本快速的老龄化存在更密切的联系,那么这是日本的数据。然后我们再来看美国的数据,美国的数据在一定程度上具有类似的特征,在2004年之前,美国房地产投资占整个GDP的比重差不多就在8%的水平。
- Key Takeaway:
- 1. Housing Bubble 的累积 <-> 一定伴随着 异常的 房地产投资增加。与存货并无相关。
- 2. Housing Bubble Collapses <-> 是房地产去库存的过程。在1阶段,房地产投资增加,带来supply增加,直到supply远大于demand,bubble collapse。
- 3. 人口结构等因素会影响 房地产库存的供求。
我们知道80年代的日本,2000年的美国都已经是一个人均收入很高度发达的经济体,也是早已经完成城市化的经济体。但是在那个条件下,我们看到他们房地产投资占整个GDP的比重还在接近8%的水平,这里的房地产有住宅,也有商业地产等等。
但是2004年以后,房地产投资的占比也开始出现了单边的上升,从8%上升到不到10%的水平,这些上升过程代表了供应的扩大,反映了在那几年的时间里边,美国房地产市场的泡沫化它上升了9%多的水平,以后,在这一位置的话停留到2007年到2008年。
随后随着泡沫的破灭,房地产投资占整个GDP的比重经历了时间较长的幅度非常大的下跌,这一下跌毫无疑问的部分是为了消化泡沫化过程之中的过剩,另外一方面它也反映了金融体系和住户的资产负债表所受到的压力。
那么直到2014、15年以后,美国的房地产市场看起来才基本稳定下来,但是一直到最近这两年,它的房地产占房地产投资占GDP的比重才勉强接近,可能还没有达到在2003年之前的水平勉强接近,但是看起来没有达到。
Ref
高善文经济观察
国企 & 私企
有个常见的说法是:国企比较有社会责任感,可以做很多私企觉得无利可图,不愿意做的事情。比如给某些偏远地区供电供水和邮政。
本质上,这种依然属于外部性。也就是从国家的角度来说,保证偏远地区的供电供水和邮政是重要的,但是私企自己又不是国家,所以不愿意去做。那么解决这个问题,其实和国企不国企并没有必然关系。
私企不愿意做是因为亏本,那么出于国家的某些需要(在这里是指的国民待遇的公平)通过国家补贴的方式,一样可以让私企来做。区别在于:私企做的时候补贴是显性的,是能看到从财政中拨款来进行补贴的;而国企做这些事情,补贴是隐性的,因为国企的利润就是政府的财政收入的一部分,所以依然相当于国家从财政收入中补贴。但是无论显性或者隐性,当其他条件不变的时候,这两者并无区别。
假定存在两个区域发达(D)和不发达(UD),提供服务的成本统一为 c。但是问题在于发达地区人们的支付意愿比较高,能从这项服务里面获得 u_d 的效用,而不发达地区的人们支付意愿比较低,能从这项服务里面获得 u_{ud} 的效用(这里如果反过来假设服务成本有区别也是一样的)。假定每个区域都有1个消费者,那么当企业无法区别定价的时候,企业有两个选择,如果只服务发达地区,那么价格可以定为 u_d ,而如果两个地区都服务,那么价格就只能定为 u_{ud} 。
在第一种情况下,企业利润为 u_d -c ,在第二种情况下,企业利润为 2(u_{ud}-c) 。那么当 c>2u_{ud}-u_d 的时候,企业就会只服务发达地区。
但是企业没有考虑的是,如果两个地区都服务,可以促进两个地区共同的经济发展,假如这个长期收益为 \pi_l ,那么显然当 \pi_l 足够大,大到弥补因为服务欠发达地区而造成的利润损失 u_d+c-2u_{ud} 的时候,国家的利益就和企业的利益不一致了。
这个时候如果政府想让私企服务不发达地区,那么就需要提供一个补贴,让私企至少能够赚的和现在一样多。这个补贴就是 u_d+c-2u_{ud}。 也就是私企因为要服务不发达地区而少赚的钱。而因为国家本身不产生任何的财富,这个补贴必然是从税款里面出。
这个时候,私企如果坚持不服务不发达地区,其获得的是: u_d -c 。而如果私企服务不发达地区,其收入是 2(u_{ud}-c) + u_d+c-2u_{ud}=u_{d}-c 。两边收益相等,私企自然愿意服务不发达地区了。
这个时候,国家和企业共同创造的价值是 \pi_l + 2(u_{ud}-c) 。欠发达地区获得了服务,发达地区获得了相对较低的价格,消费者还能剩下 u_d – u_{ud} 。所以社会总剩余就是 u_d + u_{ud}-2c+\pi_l 。
那么国企呢?国企直接被命令服务于这两个地区,其总利润是 2(u_{ud}-c) ,消费者剩余和上面一样,国家同样实现了长期收益,所以社会总剩余还是 u_d + u_{ud}-2c+\pi_l 。国企虽然不需要补贴,但是收入本来就降低了,依然相当于是隐形的补贴出去了。
这两者是完全一样的。因为说到底,消费者在两个模型下得到了同样的服务,企业供应了同样的产出,效率是完全一样的。
私企有时候不愿意承担社会责任,因为花的是自己的钱,去做亏本买卖心不甘,但是只要提供足够的补贴,那么照样可以做;而国企承担社会责任,本身就已经包含了国家的补贴。资源不是无中生有的,国企亏本做事情,最后买单的依然是政府,而政府本身不产生财富。
但是根据我们的观察,在现实中,国企和私企确实存在区别。那么肯定是有不一样。不一样在什么地方呢?其实说到底,还是一个科斯定理的问题:交易成本。
在国企-私企上面这个简单的模型里面,里面假定了是没有任何交易成本,并且合同是一定执行的,那么这个时候产权本身就是不重要的。但是现实中显然不能满足这个条件。
首先是收税的成本。
假定国企和私企赚的利润都一样。因为政府本身就是国企的事实拥有者,那么可以直接的把国企的利润变成政府的收入。但是私企不一样,私企因为所有者和政府不同,那么就存在少交税的动机。要获得同样的收入,就需要雇佣人手查税。这样就存在了一个因为税务信息不对称,而产生的交易成本。
比如说,在上面的例子里面,政府给私企的补贴,是要靠收税收上来的。那么收税需要人手,需要雇员,还需要查账。如果存在一个 λ ,国家每收上来1的税,其消耗的资源是 (1+λ) ,那么这个就是补贴私企的过程中所带来的额外损耗。但是强行命令国企去做亏本生意,则相当于补贴原地生效,就不存在上面这个问题。
其次是多任务激励。
大的私企的经理人和国企经理人都存在道德风险的问题,这是所有者和经营者分离的企业所共有的问题。但是这个问题在国企和私企之间还是不一样的。
私企的目标相对比较明确,更看重利润,而解决道德风险(经理人偷懒、吃里扒外)的问题主要是通过合同设计,所谓重赏之下必有勇夫,在给出高额的激励合同之后,经理人和股东之间的利益还是能够达成某种程度上的一致。
但是国企的经营目标是多元的。有经济上的,有政治上的。有容易量化的,有不容易量化的。那么这个时候国企的经营者就更有动机去根据自己的利益,而非政府的利益来平衡自己所付出的努力。平常说的「形式主义」,为什么在国企会比较突出一些?因为当努力的程度不可观测的情况下,「形式」恰恰是可以量化的,更容易被观测到的。
这只是其一。其二就是国企的升职路径是排他的——私企在市场上竞争,虽然说也是互相争夺市场份额,但是彼此之间有一个正的外部性,那就是大家的努力可以共同把市场做大。但是国企的高管竞争的是行政职位,而行政职位是零和的。这意味着强的激励更容易导致管理人员之间的互相破坏。与此同时,因为多任务并行,对绩效的考核,和真实的效率之间就更容易出现误差。
假定有两个努力方向, 一个同时和绩效标准和真实效率有关,一个只和真实效率有关,但是和绩效考核标准关系不大。那么显然管理者就更容易只对着和绩效相关的地方去努力。
这些都是环环相扣的,正是因为国企需要同时兼顾市场和政令,所以就导致国企无法像私企那样给一个很高的激励体制给自己的经理人——因为这样只有两个可能:要么因为激励太强,导致国企的管理人员「不听话」了,要么因为激励给偏了,从而导致真实的效率还不如低激励的时候。
并且国企的经营者还面临着激励一致性不足的问题。私企无论谁当股东,都希望自己公司的市值越来越高,公司资产越来越多;但是国企经营者的行政领导往往是有任期的,而行政领导的任期和企业的经营周期并不重合。
不同的领导,甚至于同一个领导在不同的时期都可能会提出不同的要求,而这些要求也并不总是能够和企业利润最大化一致。而管理人员对这一点是有预期的。那么在制定长期规划的时候就会尽量的保守,以免领导更换之后,面临巨大的沉没成本要负责的问题。
最后还有一点是和科斯定理有关的,那就是在完成政府目标这方面,「国企」相比私企比较好用,背后所反映的是两种激励之间的权衡。国企对经营者的激励是官僚层级上的提升,也就是内部晋升,而私企对经营者的激励是市场报酬。如果内部晋升更加的好用,那么有两种可能的解释:
第一种可能的解释是内部组织非常的精炼和高效,所以激励更强,应该进一步扩大;第二种解释是说明整体外部市场的有效程度还很不够,摩擦力太大,以至于通过政策+补贴的市场化激励还不如内部的行政命令。
Reference
https://www.zhihu.com/question/301294803/answer/2812237308
Gradient / Derivative in Python
By definition:
$$ \nabla f(x_1, x_2) =\frac{\partial f}{\partial x_1} + \frac{\partial f}{\partial x_1} $$
$$ \frac{\partial f}{\partial x_1} = \lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h} $$
$$ \frac{\partial f}{\partial x_1} = \lim_{h\rightarrow 0}\frac{f(x+h)-f(x-h)}{2h} $$
- Code:
func_1 = lambda x: x**2 +5
func_2 = lambda x: x[0]**2 + x[1]**3 +1
x_lim = np.arange(-5,5,0.01)
input_val = np.array([2.0,3.0])
class Differentiate:
def __init__(self):
self.h = 1e-5
self.dx = None
def d1_diff(self, f, x):
fh1 = f(x+self.h)
fh2 = f(x-self.h)
self.dx = (fh1 - fh2)/(2*self.h)
return self.dx
def tangent(self, series, f, x_loc):
"""
Return a Tangent Line, for ploting.
"""
y_loc = f(x_loc)
self.d1_diff(func_1, x_loc)
b = y_loc - self.dx * x_loc
y_series = self.dx * series + b
return y_series
# for f(x1, x2, x_3, ...)
def dn_diff(self, f, x):
grad = np.zeros_like(x)
for i in range(len(x)):
temp_val = x[i]
x[i] = temp_val + self.h
fxh1 = f(x)
x[i] = temp_val - self.h
fxh2 = f(x)
grad[i] = (fxh1 - fxh2) / (2*self.h)
x[i] = temp_val
self.dx = grad
return self.dx
def gradient_descent(self, f, init_x, lr = 0.01, step_num = 1000):
x = init_x
for i in range(step_num):
self.dn_diff(f, x)
x -= lr * self.dx
return x