For the preparation of Quants
1. Functions Definition
1.1 Each x has only one y
A function denoted f (x) of a single variable x is a rule that assigns each element of a set X ( written x \in X ) to exactly one element y of a set Y ( y\in Y) :
$$
y=f(x)\quad or \quad x\rightarrow f(x)
$$
1.2 Domain of f
$Dom f$ Domain of Function
$Im f$ Image of Function
For a given value of x, there should be at most one value of y.
1.3 Implicit Form f(x,y)=0
For example,
$$
4y^4-2y^2x^2-yx^2+x^2+3=0
$$
1.4 Polynomials
$$
y=f(x)=a_0+a_1x+a_2x^2+…+a_nx^n
$$
2. Implicit Differentiation
For example,
$$
y=a^x
$$
Mainly two ways to take derivatives,
$$
ln(y)=ln(a^x)=xln(a) \
\frac{1}{y}\frac{dy}{dx}=ln(a)\quad\text{by taking derivatives to x}\
\Rightarrow \frac{dy}{dx}=y\cdot ln(a) \
$$
and plug y=a^x inside
$$
\frac{dy}{dx}=a^x\cdot ln(a)
$$
Or, simply we apply the exponential transformation, and take deriviatives later.
$$
y=e^{ln(a^x)}=e^{x\cdot ln(a)}
$$
However, for a polynomial, we normally have to do the implicit differentiation.
$$
4y^4-2y^2x^2-yx^2+x^2+3=0 \\
16y^3y’-(4y’yx^2+4y^2x)-(y’x^2+2yx)+2x=0 $$
$$(16y^3-2yx^2-x^2)y’=-2x+4y^2x+2xy \\
\Rightarrow y’=\frac{-2x+4y^2x+2xy}{16y^3-2yx^2-x^2}
$$
3. L ‘Hospital’s Rule & Limitations
If there is a limitation (, which is called as the inderterminate form),
$$
\lim_{x \rightarrow a} \frac{f(x)}{g(x)}\equiv \frac{0}{0} \ or \ \frac{\infty}{\infty}
$$
then, it could be calculated as,
$$
\lim_{x \rightarrow a} \frac{f(x)}{g(x)}=\lim_{x \rightarrow a} \frac{f'(x)}{g'(x)}=\lim_{x \rightarrow a} \frac{f”(x)}{g”(x)}=…=\lim_{x \rightarrow a} \frac{f^{(n)}(x)}{g^{(n)}(x)}
$$
For example, \frac{sin(x)}{x}, at x \rightarrow 0.
4. Taylor Series
Approximate a function a certain point, by a series of terms.(detailing explaination sees Blog Section 6 )
We use the 1st, 2nd, 3rd, 4th, … n^th derivatives, etc, to approximate the function at a certain value.
$$
f(x)\approx f(x_0)+(x-x_0)f'(x)|_{x=x_0}+\frac{1}{2}(x-x_0)f”(x)|_{x=x_0}+…+\frac{1}{n!}f^{(n)}(x)|_{x=x_0}(x-x_0)^n
$$
For example, e^x at x=0.
$$
e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+…+\frac{x^n}{n!}
$$
5. Integration
5.1 Intergration by Parts
$$
y=u(x)v(x) \
y’=u’\cdot v +u\cdot v’ \
u’v=y’-uv’ \
$$
and then integrate from both sides,
$$
\int u’v dx=\int y’ dx-\int uv’ dx
$$
as \int y’ dx = y+C, so we would get,
$$
\int u’v\cdot dx=\int v\cdot du=y-\int u\cdot dv +C
$$
For example,
$$
\int xe^x\cdot dx=\int x\cdot de^x \
=xe^x-\int e^x\cdot dx +(C) \
=xe^x-e^x+(C)
$$
5.2 Reduction Formula
We define a integral, (I_n is called Gamma Function)
$$
\int_0^{\infty}e^{-t}t^n\cdot dt= I_n
$$
$n$ is determined as the subscript of $I_n$, and could be treated as a constant in that integral.
We integrate that formula, and would get,
$$
n\int_0^{\infty}e^{-t}t^{n-1}dt=I_n \
n\cdot I_{n-1}=I_n
$$
If we keep doing that, we would get,
$$
I_n= n\cdot I_{n-1}=n(n-1)I_{n-2}=…=n!\cdot I_0
$$
where,
$$
I_0=\int_0^{\infty}e^{-t}\cdot dt=1
$$
so we get,
$$
I_n=n!\cdot I_0=n!
$$
5.3 Other Tips
5.3.1 ln|f(x)|
$$
\int \frac{f'(x)}{f(x)}=ln|x|+C
$$
For example,
$$
\int \frac{x}{1+x^2}dx\
=\frac{1}{2}\int\frac{1}{1+x^2}dx^2=\frac{1}{2}\int\frac{1}{1+x^2}d(1+x^2) \
=\frac{1}{2}ln|1+x^2|+C
$$
5.3.2 Decompose the Fraction – Factorisation
For example,
$$
\frac{1}{(x-2)(x+3)}=\frac{A}{x-2}+\frac{B}{x+3}\
A=\frac{1}{5},\quad B=-\frac{1}{5}
$$
The further implication is that.
Any rational expression \frac{f(x)}{g(x)}, ( with degree of f(x) < degree of g(x)), could be rewritten as.
$$
\frac{f(x)}{g(x)}\equiv F_1+F_2 +…+F_k
$$
, where each F_i Is,
$$
F_i=\frac{A}{(px+q)^m}\quad or\quad \frac{Ax+B}{(px+q)^m}
$$
6. Complex Number – i
6.1 Definition
$$
z=x+iy\
i=\sqrt{-i}\quad, i^2=-1
$$
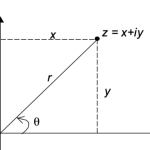
and z could be expressed in polar co-ordinate form as,
$$
z=r(cos \theta+i\ sin\theta)
$$
, where
$$
x=r\ cos\theta \quad, y=r\ sin\theta
$$
The set of all complex numbers is denoted \mathbb{C}; and for any complex number z, we could write z \in \mathbb{C}. ( \mathbb{R} \subset \mathbb{C} ).
6.2 Modulus
The modulus of z donates |z| is defined as,
$$
|z|=r=\sqrt{x^2+y^2}
$$
6.3 Complex Conjugate
$$
\bar{z}=x-iy
$$
For example, if z=x+iy, then \bar{z}=x-iy.
6.4 Polar Form
$$
z=r(cos\ \theta+i\ sin \ \theta)=re^{i\theta}
$$
by Euler’s Identity,
$$
e^{i\theta}=cos\ \theta+i\ \sin\ \theta \
e^{-i\theta}=cos\ \theta-i\ \sin\ \theta \
|z|=r,\quad arg\ z=\theta
$$
6.5 Euler’s Formula
The Euler’s Identity is shown as, by applying Taylor’s Expansion and by i^2=-1,
$$
e^{i\theta}=1+i\theta+\frac{(i\theta)^2}{2!}+…+\frac{(i\theta)^n}{n!}\
=(1-\frac{\theta^2}{2}+\frac{\theta^4}{4!}+…)+i\times(\theta-\frac{theta^3}{3!}+\frac{\theta^5}{5!}+…) $$
$$=cos\ \theta +i\ \sin\ \theta$$
Plug \(\theta = \pi\) into Euler’s Formula,
$$
e^{i\pi}=cos\ \pi+ sin\ \pi\
e^{i\pi}=-1
$$
7.Higher Derivatives
$$
\frac{\partial^2 f}{\partial x^2}=f_{xx}=\frac{\partial}{\partial x}(\frac{\partial f}{\partial x}) \ \
\frac{\partial^2 f}{\partial x \partial y}=f_{xy}=\frac{\partial}{\partial y}(\frac{\partial f}{\partial x}), $$
\(f_{xy}=f_{yx}\) Sequence no matters if 2nd derivatives exist and continuous.