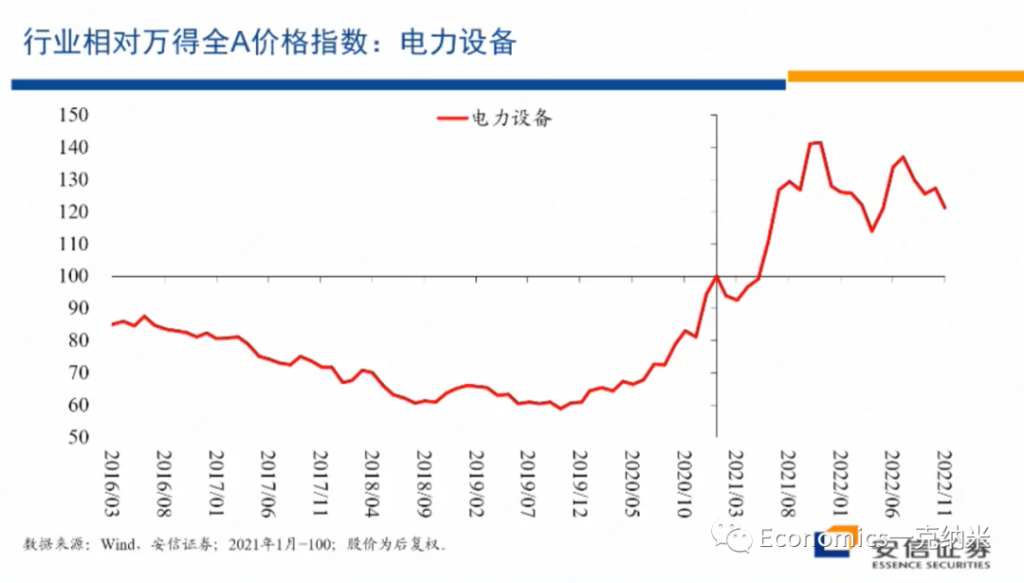
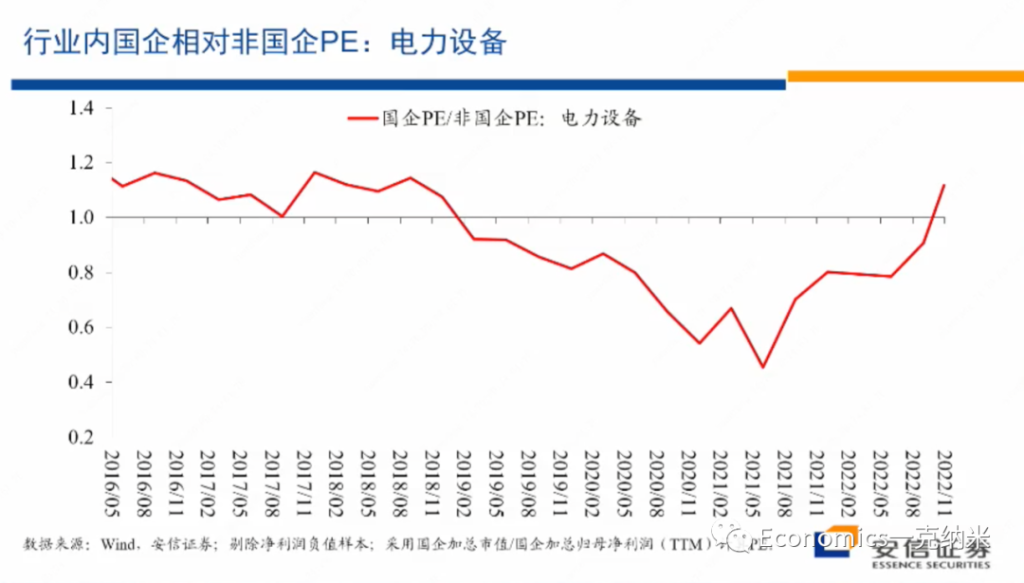
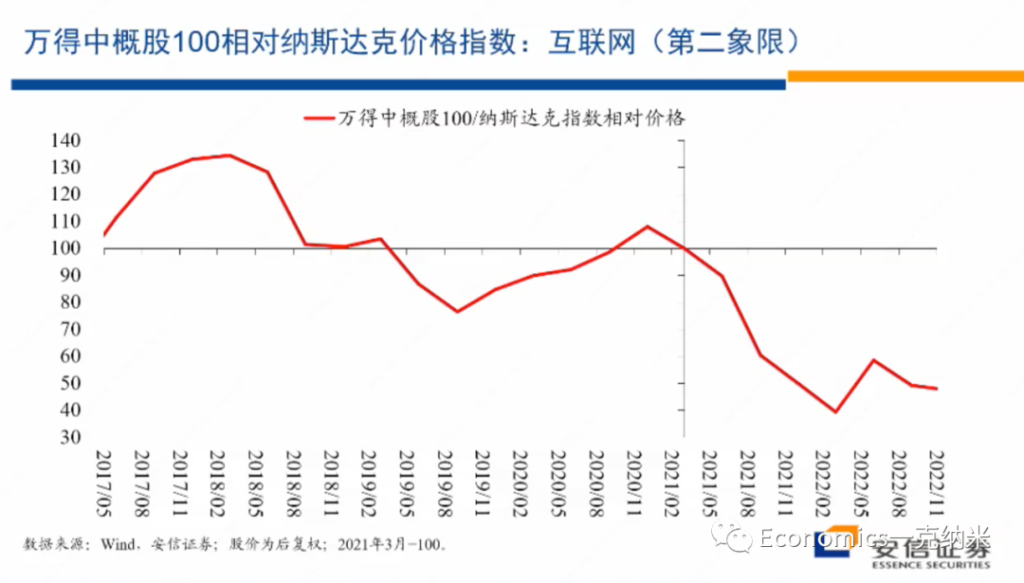
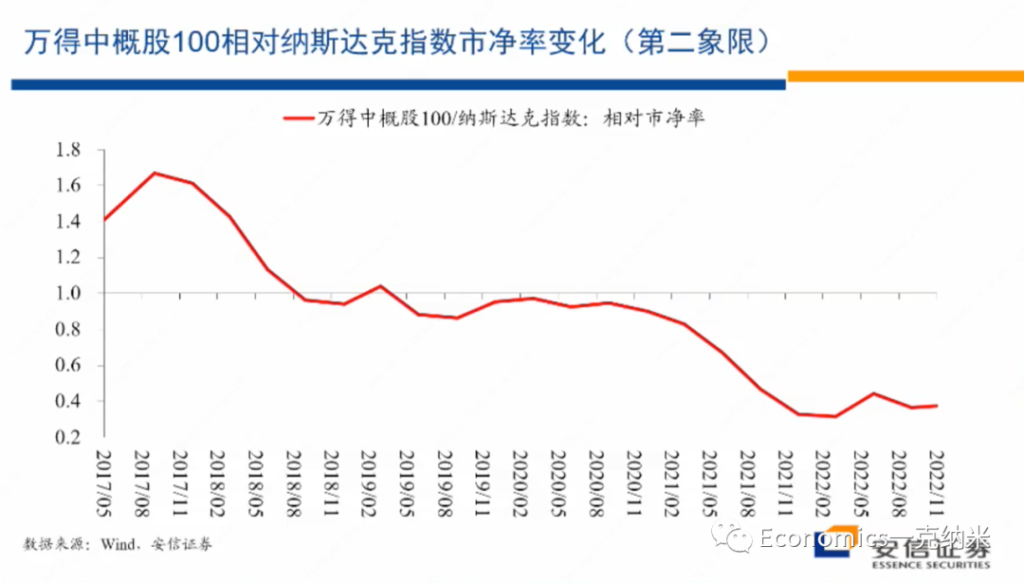
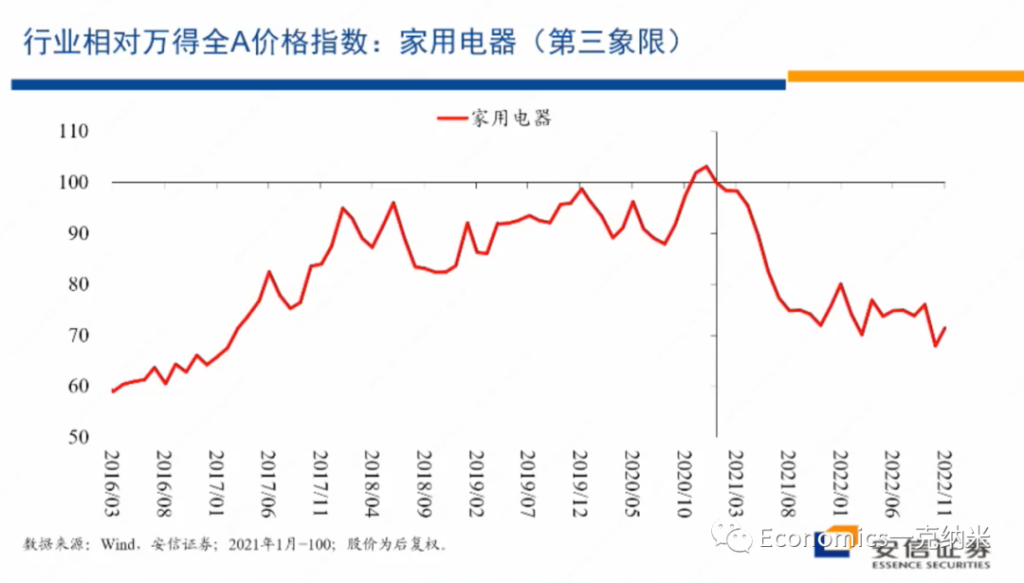
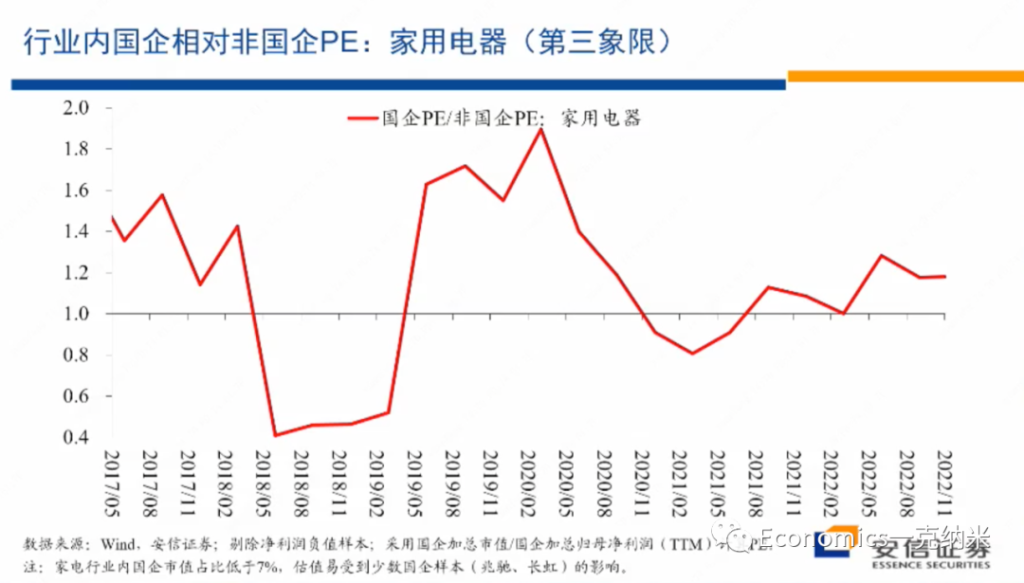
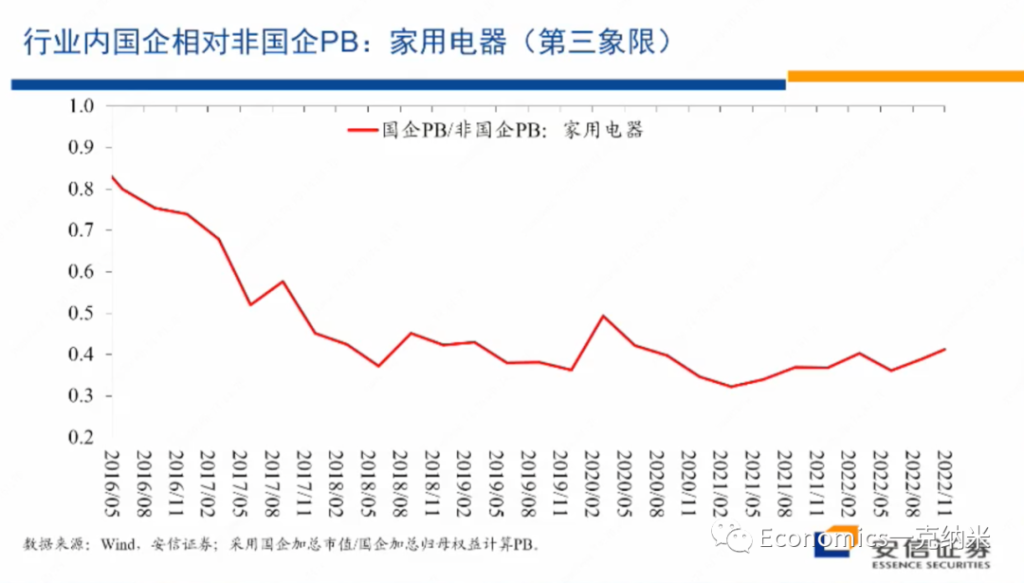
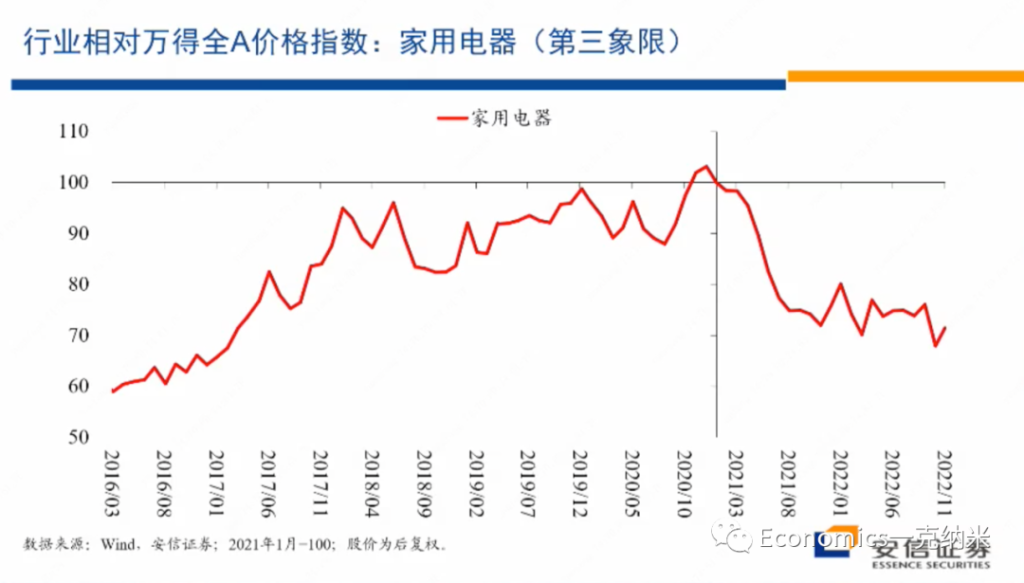
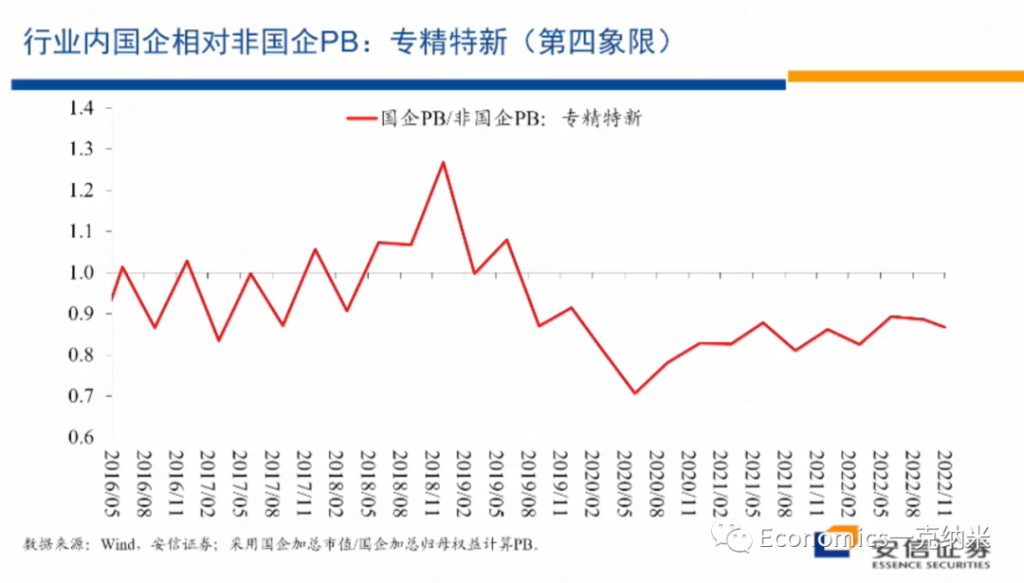
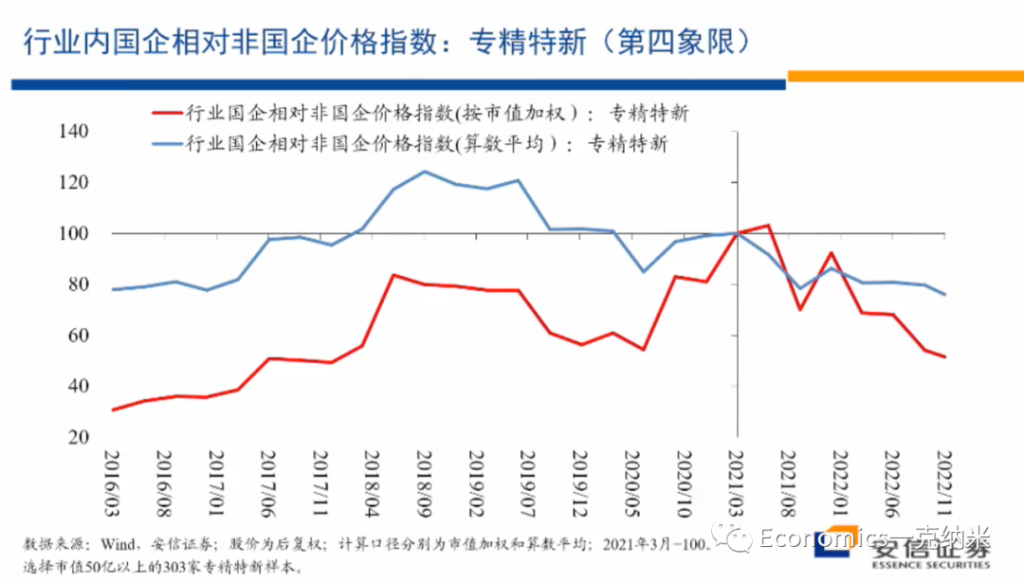
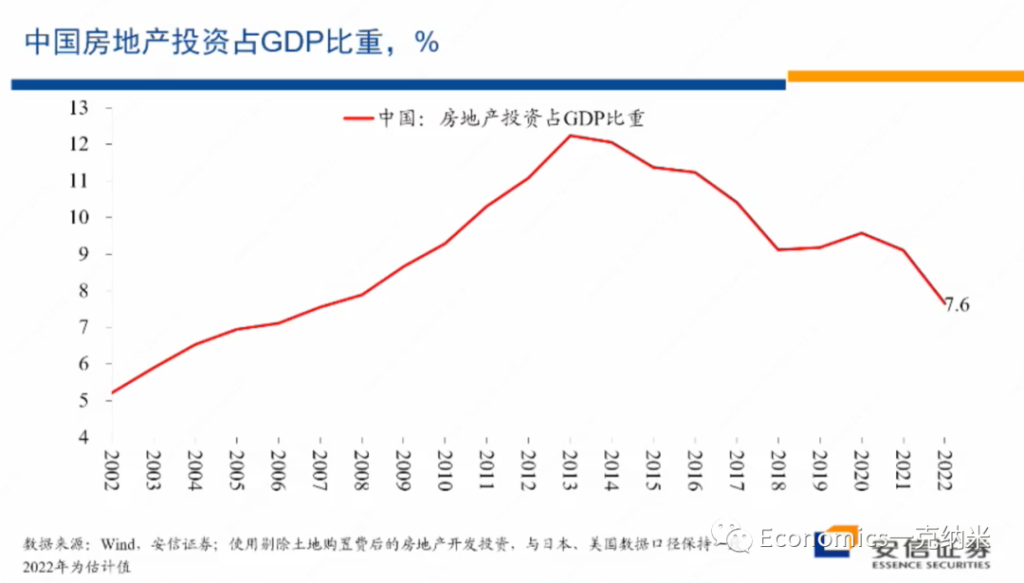
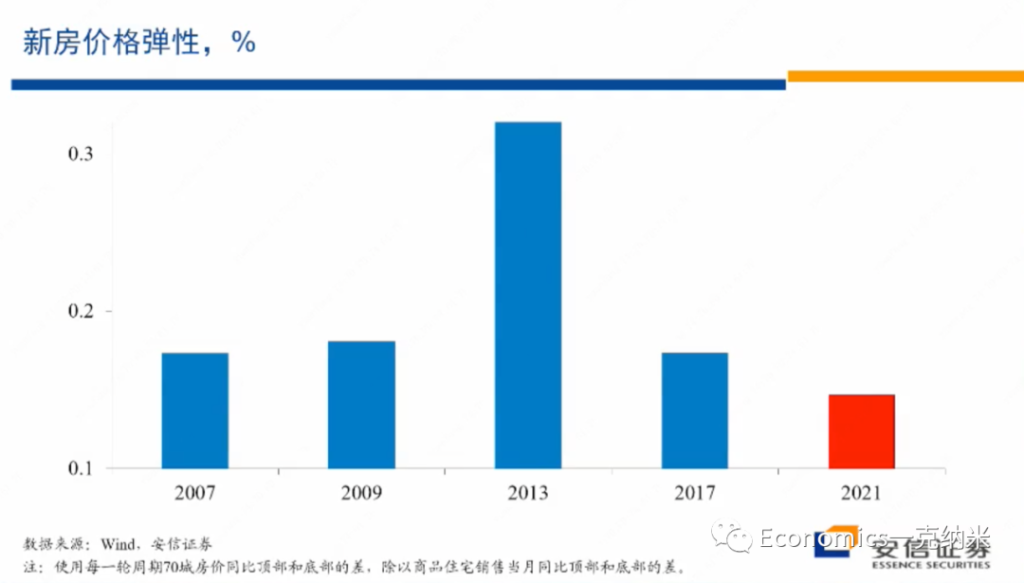
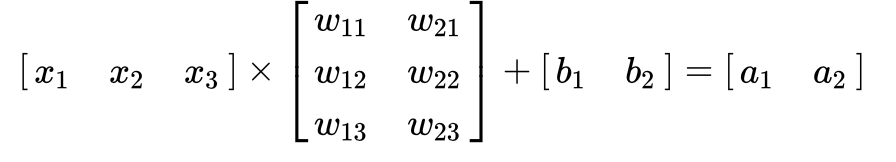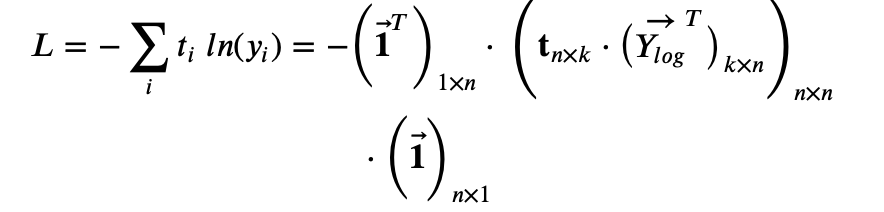摘要:实证资产定价已然进入因子(协变量)的高维数时代。本文抛砖引玉,阐述我对此的四点思考。(DGP: Data Generating Process)
- Key Takeaway: over-parameterization 的时代已经到来,变量数量 k 大于样本数量 t 似乎并没有带来 interpolate的问题,反而给prediction带来了帮助。
0 引子
时至今日,实证资产定价(以及因子投资)已然步入了因子(协变量)的高维数时代。大量发表在顶刊上的实证结果表明,多因子模型具有很大的不确定性且因子的稀疏性假设不成立。人们熟知的 ad-hoc 简约模型无法指引未来的投资。
在高维数时代,寻找真正能够预测预期收益率的协变量是核心问题之一。为了实现这个目标,需要考虑的问题包括:(1)多重假设假设检验;(2)投资者(高维)学习问题 & 另类数据;(3)来自资产定价理论的指引:即解释预期收益率的因子应该也能解释资产的共同波动。最后,一个最新的讨论热点是因子的个数是否越多越好(即模型复杂度是否越高越好):复杂模型能更好地逼近真实 DGP,但参数估计的方差更大;简约模型的参数估计更准确,但却未必是 DGP 的合理近似。二者相比,如何权衡呢?
近日,我在某券商 2023 的年度策略会上做了题为《因子投资的高维数时代》的报告,阐述了我对上述四点的思考。本文借着报告的 slides 做简要介绍。由于对于某些问题专栏已经做了大量的梳理(比如多重假设检验),因此在本文的阐述中,在必要的地方会使用最少的文字(你马上就会明白我的意思)。
1 多重假设检验
这部分,一图胜千言。需要相关知识的小伙伴,请查看公众号的《出色不如走运》系列。
Next.
2 投资者学习问题 & 另类数据
理性预期假设投资者知道真实的估值模型。
然而,和进行事后(ex post)因子分析的你我一样,投资者在投资时同样面临协变量的高维数问题,因此不可能知道真实的估值模型,所以理性预期假设并不成立。这造成的结果是,均衡状态下资产价格和理性预期情况下相比出现偏差。在事后分析中,已实现收益率中包含一部分因估计误差导致的可预测成分。但对投资者来说,事前(ex ante)无法利用上述可预测性。
因误差导致的可预测性能够在样本内(IS)产生虚假的可预测性(无论投资者是否使用了先验以及无论先验是否正确),而在样本外(OOS)却无法预测收益率。这就是投资者(高维)学习问题导致的虚假的可预测性(Martin and Nagel 2022)。具体阐述见《False In-Sample Predictability ?》。面对这个问题,需要通过 OOS 检验才能规避。

投资者无法在事前投资中应对高维数,这主要体现在他们使用较少的协变量(因子)作为估值的依据。另一方面,由于一些变量的获取成本很高,投资者需要在该变量带来的预测好处和其成本之间权衡。此外,有限理性中的有限注意力机制也为投资者对简约性的渴望提供了微观基础。这两方面作用合力导致投资者在为资产定价时使用过度稀疏的估值模型。这样做的后果是,即便在样本外,也会出现因投资者学习问题而造成的虚假的可预测性。
就着上述推论,我们自然地引出本小节的另一个相关话题:另类数据。
回忆一下公众号之前的文章《科技关联度II》所介绍的 Bekkerman, Fich and Khimich (forthcoming)。相比于之前的基于专利类别的研究,该文对专利进行文本分析,通过提取专业术语并计算其重合度来描述公司之间的相似程度,以此构造了预期超额收益率更高的科技关联度效应。
比起专利类别,投资者在获得以及处理专利文本并计算科技关联度时的成本更加昂贵。这会导致大多数投资者会在为公司估值时忽略这方面的信息,即使用过度稀疏的估值模型,造成样本内和样本外收益率可预测性。
该文基于文本分析的科技关联度是近几年大红大紫的基于另类数据进行实证资产定价和因子投资的一个典型例子。然而,Martin and Nagel (2022) 所勾勒出的非理性预期假设世界告诉我们,使用最新的方法和技术构建预测变量并将其应用于早期历史时段时,它们在样本内和(伪)样本外检验中均能预测预期收益率。因此,我们在惊喜于另类数据的发现之余,恐怕也应该多一分谨慎。
除此之外,既然谈到另类数据,不妨再聊聊另一个相关话题。有相关研究表明,海外大量的另类数据供应商提供的数据都只具备对公司基本面的短时间尺度的可预测性。Dessaint, Foucault and Fresard (2020) 的研究表明,如此另类数据可得性的提升降低了进行短时间尺度的预测成本(从而提高了准确性),但增加了进行长时间尺度预测的成本(从而降低了准确性)。对于公司基本面预测来说,二者的综合效果是 mixed。可以预见,未来在使用另类数据预测公司基本面时,会有更多的研究向这个方向倾斜。
3 和协方差矩阵有关
Ross (1976) 的 APT 指出,解释资产预期收益率截面差异的因子应该同时能够解释资产的共同运动。在市场中不存在近似无风险套利机会这个假设下,Kozak, Nagel and Santosh (2018) 同样论述了这一点(见《Which beta (III)?》)。
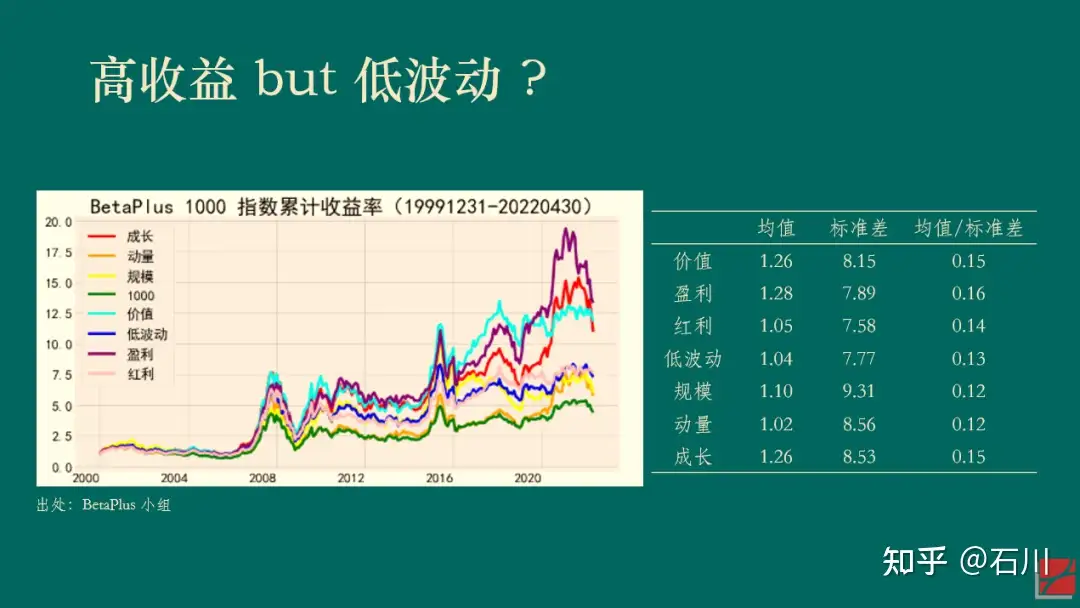
以下展示了 BetaPlus 小组构造并维护的 A 股常见七类风格因子在 2000/01/01 到 2022/04/30 之间的表现。统计数据表明,在该实证区间内,虽然它们的收益率均值高低有差异,但收益率的标准差同样也有差异,因此并没有哪个风格因子的风险调整后收益明显高于其他的因子。
再来看一个美股的例子。Kozak, Nagel and Santosh (2018) 将实证区间分成前后两半儿并考察了 15 个因子。下图展示了每个因子在前后两个区间内夏普率的散点图。如果能够在获得高收益的同时降低波动,那么样本内(前一半区间)夏普率高的因子在样本外(后一半区间)的夏普率应该仍然更高一些,我们将会看到这些点围绕在 45 度直线上。然而事实并非如此。无论样本内的夏普率多高,这 15 个因子样本外的夏普率几乎是一条平行于横坐标的水平线,而非人们期望的 45 度斜线。(我用几百个因子在 A 股做了同样的实证,观察到了类似的结果。)
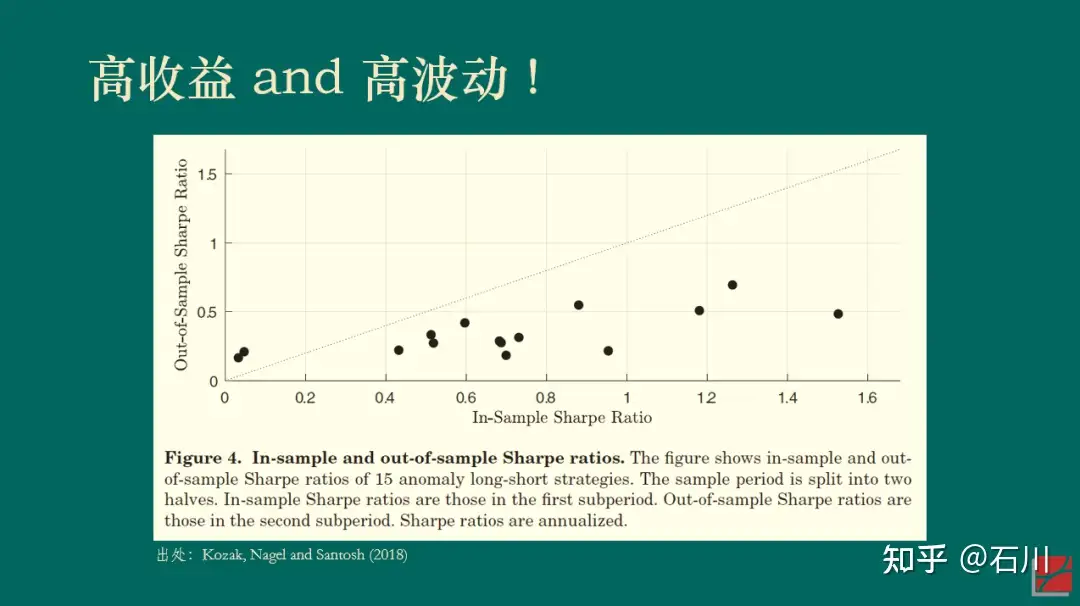
上述结果显示,(样本外)高收益往往对应着高波动(对着样本内硬挖 —— data snooping —— 另说),这一实证结果和 APT 吻合。
早在几十年前,Eugene Fama 曾经打趣到 APT 让众多挖因子的尝试“合理化”,即 APT 只说了资产预期收益率和众多因子有关,但却没有指出到底有哪些因子。因此,很多学者打着 APT 的旗号“肆无忌惮”地挖出了一茬又一茬因子(zoo of factors),Fama 把这个现象称作 APT 给了这些研究“fishing license”(即 APT 让这些研究合理化)。(Sorry,这里我实在忍不住吐槽一句,在一本著名的资产定价教材的中译版中,中文作者竟然真的把 fishing license 翻译成“钓鱼许可证”……)
如今,当我们重新审视 APT 时,毫无疑问应该将它作为挖掘真实因子的有效指引,正如本节一开头说的那样:解释资产预期收益率截面差异的因子应该也能解释资产的共同运动。在这个认知下,以 PCA 为代表的一系列实证资产定价研究在这几年取得了很多突破(Kelly, Pruitt and Su 2019 、Kozak, Nagel and Santosh 2020)。
4 越复杂越好 ?
在本节的讨论中,我们以因子个数的多少代表模型复杂度。因子个数越多,模型越复杂。
2019 年,Belkin, et al. (2019) 一文提出了机器学习中样本外误差的“double descent”现象,引发了机器学习领域和理论统计领域的广泛讨论。为了理解这一现象,我们先从熟知的 bias-variance trade-off 说起。
对于模型来说,其样本外表现和模型复杂度关系密切。当模型复杂度很低时,模型的方差很小(因为变量参数估计的方差很小),但是偏差很高;当模型复杂度高时,模型的方差变大,但是偏差降低。二者的共同作用就是人们熟悉的 U-Shape,即 bias-variance trade-off,因此存在某个最优的超参数,使得样本外的总误差(风险)最低。
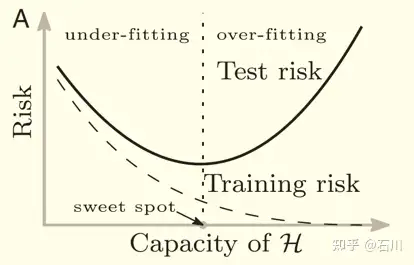
我们还可以换个角度来理解 bias-variance trade-off,而这个角度对理解 double descent 至关重要。当模型很简单时,它能够有效规避过拟合,但却很难想象如此简单的模型是真实世界的好的近似;而当模型复杂时,它更有可能逼近真实世界,但是也的确更容易过拟合。因此 bias-variance trade-off 也可以理解为 approximation-overfit trade-off。
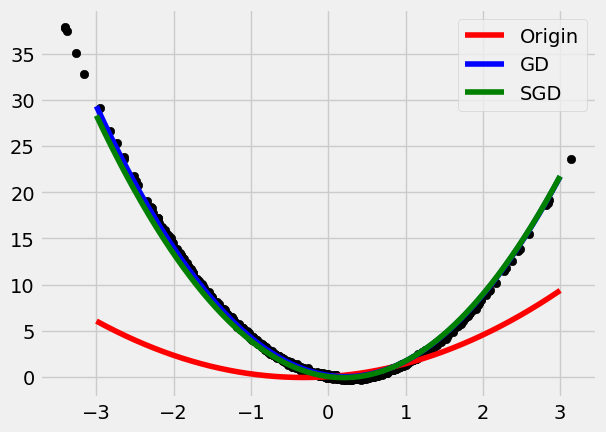
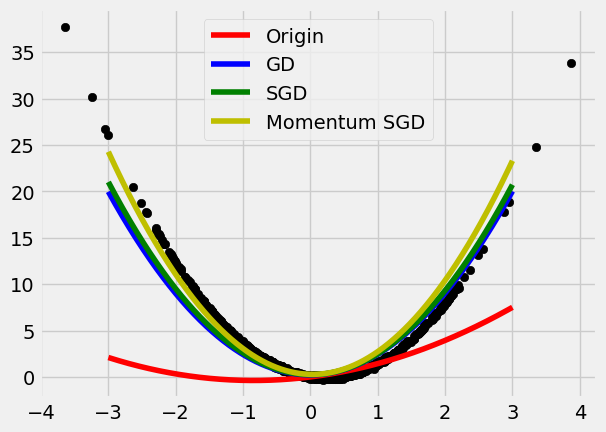
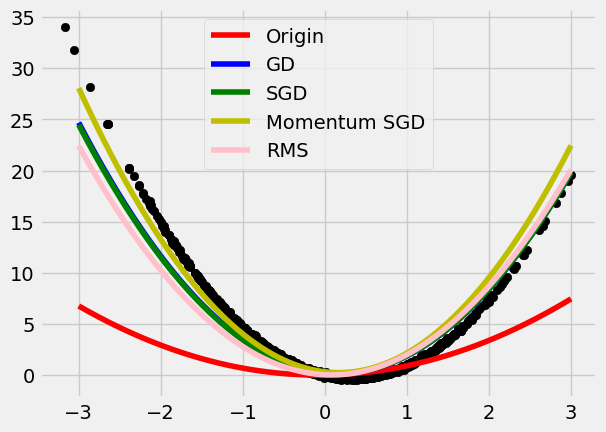
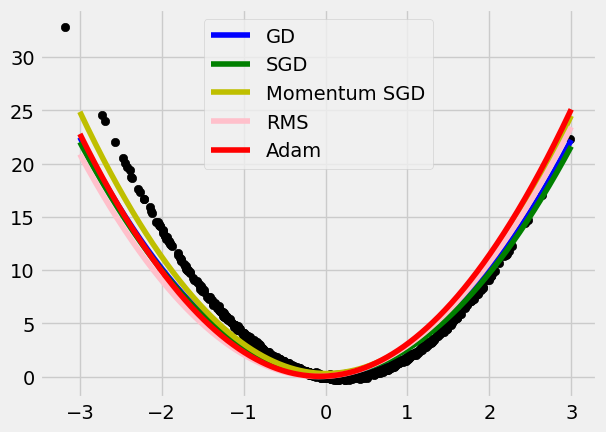
然而,上述结论有一个我们都习以为常的前提:变量个数 < 样本个数。那么,如果模型复杂到变量(因子)的个数超过了样本的个数又会出现怎样的情况呢?事实上,这一问题并非无缘无故的凭空想象。对于复杂的神经网络模型来说,模型参数的个数很容易超过样本的个数,然而这些模型确在样本外有着非凡的表现(哦,当然不是资产定价领域)。这个现象促使这人们搞清楚 what is behind the scene。
当变量个数 > 样本个数时,模型在样本内能够完美的拟合全部样本(在机器学习术语中,这个现象被称为 interpolation)。对这样一个模型来说,人们通常的认知是,它在样本外的表现一定会“爆炸”,即毫无作为。这是因为它过度拟合了样本内数据中的全部噪声。然而,Belkin, et al (2019) 指出,当人们让模型复杂度突破样本个数这个“禁忌之地”后,神奇的事情发生了:样本外总误差并没有“爆炸”,而是随着复杂度的提升单调下降。正因为在样本个数两侧都出现了误差单调下降的情况,Belkin, et al (2019) 将这个现象称为 double descent。
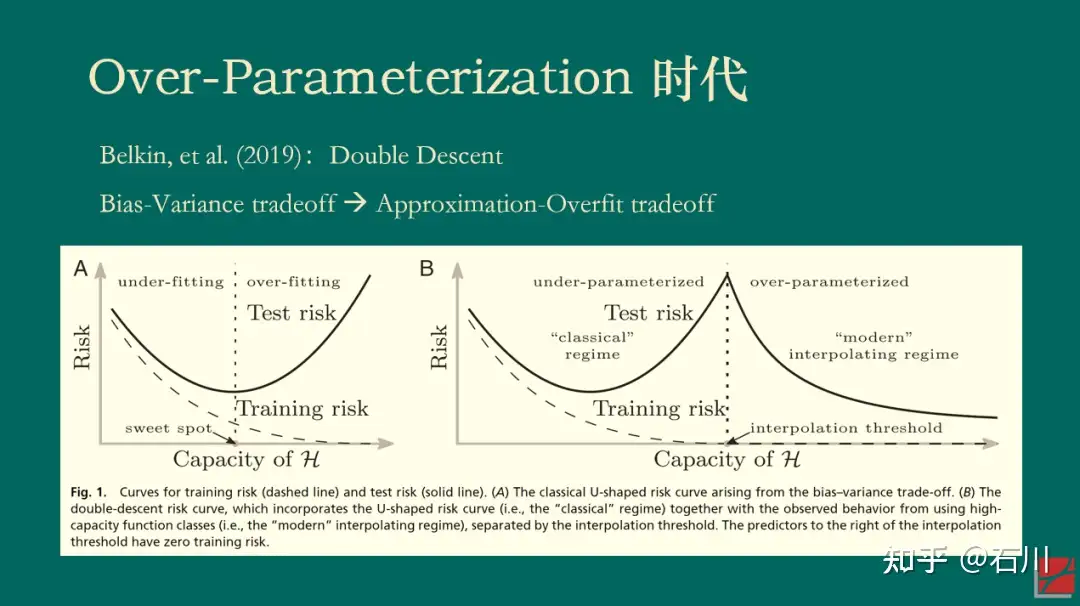
因为本文的目的并非解释背后的统计学理论,所以我在此对该现象给一些直觉上的解释。当变量个数超过样本个数的时候,样本内的解是不唯一的,而最优的解可以理解为满足参数的方差最小(正则化或 implied 正则化在这个过程中发挥了非常重要的作用)。随着变量越来越多,最优解的方差总能单调下降。
再来看偏差,通常来说,偏差确实会随着复杂度的提升而增加。但是所有模型都是真实 DGP 的某个 mis-specified 版本。当存在模型设定偏误的时候,可以证明当变量个数超过样本个数时,偏差也会在一定范围内随着复杂度而下降。因此,二者的综合结果就是模型在样本外的误差表现会随复杂度的上升而下降。(在一些情况下,样本外误差的 global minimum 出现在当变量个数 > 样本个数时。)
以下两张 slides 总结了上面的话(第二张 slide 里的表参考了 Bryan Kelly 的 talk,特此说明)。


对于资产定价和因子投资来说,如果你和我一样认同因子的高维数时代 —— 即收益率的 DGP 包含了非常多的因子,那么上述关于模型复杂度的探讨也许会带来全新而有益的启发。在这方面,也有大佬已经走在了前面。Bryan Kelly 和他的合作者以及学生一起写了一系列“复杂度美德”的 working papers,在资产定价领域探索提升复杂度带来的样本外好处。例如,Kelly, Malamud and Zhou (2022) 一文使用神经网络对美股进行了择时(每次建模仅利用一年 12 期的数据训练神经网络),并发现了类似的 double descent 现象。
当然,即便我们认同了“越复杂越好”,也依然要回答更重要的问题,即如何估计参数,如何正则化,如何来利用成千上万甚至更多的因子来形成关于预期收益率更好的预测。虽然 Kelly 等人的文章在择时方面取得了让人兴奋的结果,但在 cross-section 是否有类似的实证结果依然需要时间来回答(Kelly 有一篇 working paper 研究 cross-section,但还没有 publicly available)。
但是无论如何,欢迎来到 over-parameterization 时代。
5 结束语
以上就是我对因子投资高维数时代的四点思考。
不过在本文的最后,仍然有必要指出,在协变量的高维数时代,如何 prepare 因子固然重要(小心多重假设检验、小心投资者学习、利用 APT 的 implication),但是如何求解高维问题才更加核心(如何利用复杂度的好处 ?)。
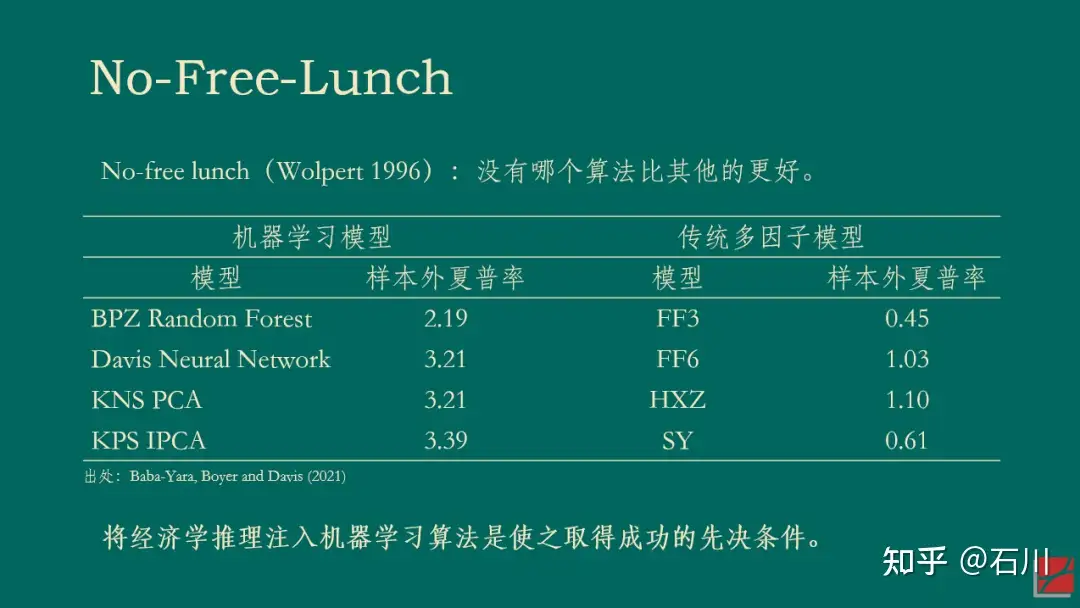
或许,我们已经到了从计量经济学到机器学习的必然转型时刻。正如 Stefan Nagel 的《机器学习与资产定价》(Nagel 2021)所倡导的那样,将经济学推理注入机器学习算法将成为高维数时代研究的必经之路。

参考文献
- Baba-Yara, F., B. Boyer, and C. Davis (2021). The factor model failure puzzle. Working paper.
- Bekkerman, R., E. M. Fich, and N. V. Khimich (forthcoming). The effect of innovation similarity on asset prices: Evidence from patents’ big data. Review of Asset Pricing Studies.
- Belkin, M., D. Hsu, S. Ma, and S. Mandal (2019). Reconciling modern machine-learning practice and the classical bias-variance trade-off. PNAS116(32), 15849 – 15854.
- Dessaint, O., T. Foucault, and L. Fresard (2020). Does alternative data improve financial forecasting? The horizon effect. Working paper.
- Kelly, B. T., S. Malamud, and K. Zhou (2022). The virtue of complexity in return prediction. Working paper.
- Kelly, B. T., S. Pruitt, and Y. Su (2019). Characteristics are covariances: A unified model of risk and return. Journal of Financial Economics 134(3), 501 – 524.
- Kozak, S., S. Nagel, and S. Santosh (2018). Interpreting factor models. Journal of Finance73(3), 1183 – 1223.
- Kozak, S., S. Nagel, and S. Santosh (2020). Shrinking the cross-section. Journal of Financial Economics 135(2), 271 – 292.
- Linnainmaa, J. T. and M. R. Roberts (2018). The history of the cross-section of stock returns. Review of Financial Studies31(7), 2606 – 2649.
- Martin, I. and S. Nagel (2022). Market efficiency in the age of big data. Journal of Financial Economics145(1), 154 – 177.
- Nagel, S. (2021). Machine Learning in Asset Pricing. Princeton University Press.
- Ross, S. A. (1976). The arbitrage theory of capital asset pricing. Journal of Economic Theory 13(3), 341 – 360.
By
石川 https://zhuanlan.zhihu.com/p/589370949?utm_medium=social&utm_oi=774013724896788480&utm_psn=1583185642497994752&utm_source=wechat_session&utm_id=0